どうも、木村(@kimu3_slime)です。
今回は、2,3次元の実数空間を例に、線形代数学の基本的なアイデアである、実数空間、線形結合、線型部分空間、次元について紹介します。
これらを通じて、線形代数学がなぜ「線形」「代数学」と呼ばれるかが伝わると嬉しいです。
前提知識:集合論入門:集合の定義、数の集合、ラッセルのパラドックス、集合論のはじまり、全称命題と存在命題、論理記号を知ろう、述語論理、量子化とは:全称記号(∀)と存在記号(∃)、数学における例と否定
実数空間:和、スカラー倍ができる
線形代数学では、点の位置を測るための区切れ目、すなわち座標(coordinate)の入った空間を考えます。

参考:集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
例えば平面上のある1点を数を使って指し示すためには、どうしたら良いでしょうか? 2つの座標軸があるので、その軸によって測った数2つで表せるでしょう。例えば、1つ目の軸\(x_1\)の方向に\(1\)、2つ目の軸\(x_2\)の方向に\(2\)の点ならば、\((1,2)\)と書けば簡単です。
集合論の言葉を使えば、平面上の点全体の集合\(\mathbb{R}^2\)は、次のように表せます。
\[ \begin{aligned}\mathbb{R}^2 := \{(x_1,x_2) \mid x_1 ,x_2 \in \mathbb{R}\}\end{aligned} \]
先程の点\((1,2)\)は、\(\mathbb{R}^2\)に属しています(\((1,2) \in \mathbb{R} ^2\))。\( \mathbb{R}\)は実数の集合を表し、自然数、整数、有理数、無理数が含まれたものです。
より一般には、\(N\)を自然数とし、実数空間\(\mathbb{R}^N\)を考えます。これはユークリッド空間、数ベクトル空間、\(N\)次元空間とも呼ばれる、線形代数学の基本的な考察対象です。
実数空間には、「空間」と呼ばれるに値する、代数的な法則が定まっています。
まず、2つの点\(x=(x_1,x_2),y=(y_1,y_2)\)は、そのそれぞれの成分が等しい\(x_1=y_1,x_2 =y_2\)とき、等しい\(x=y\)と考えます。このような数の組\((x_1,x_2)\)は、数が並ぶ順序を考慮に入れているので、一般に順序対、順序組と呼ばれるのでした。
そして2つの点は、足し合わせたり、定数倍(スカラー倍)することができます(ベクトル加法とスカラー乗法)。
\[ \begin{aligned}x+y:= (x_1+y_1,x_2+y_2),\quad c x:= (cx_1,cx_2)\end{aligned} \]
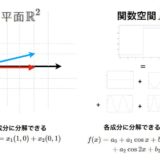
こうした計算規則によって、点\(x=(x_1,x_2)\)は原点\(o=(0,0)\)を基準とした向きを持った量、すなわちベクトルとみなすことができます。ベクトルの和はベクトルをつなぎ合わせることで、スカラー倍は引き伸ばすことです。
より一般に、このような和とスカラー倍という演算が備わった集合を、線形空間(linear space)、またはベクトル空間(vector space)と言います。実数空間\(\mathbb{R}^N\)は線形空間です。
線形と呼ばれる理由は、後に線型部分空間、非線形な対象を知ることで、より明解に理解できるでしょう。
線形結合:ベクトルのコンビネーション
線形空間におけるベクトルの基本的な操作は、和とスカラー倍である、という話をしました。
例えば\(\mathbb{R}^N\)におけるベクトルが2つ\(x,y\)あったとして、それを組み合わせることで多くのベクトルを生み出すことができます。例えば、\(2x\)は\(x\)を2倍に引き伸ばしたベクトル、\(-y\)は\(y\)を反対方向へ伸ばしたベクトル。そして、\(2x-y\)はそれらを組み合わせたものです。
\(2x,-y,2x-y\)は、ベクトル\(x,y\)の線形結合であると呼ばれます。より一般に、\(c_1,c_2\)をスカラーとして、\(c_1x+c_2y\)と表されるベクトルを、\(x,y\)の線形結合(linear combination)と呼びます。線形的な組み合わせとも言えますね。
より一般には、\(k\)個のベクトル\(v_1,\dots,v_k\)の線形結合は、\(c_1 v_1+\cdots+c_k v_k\)で表されるベクトルのことです。
何か基準となるベクトルをいくつか決める。それらを線形的に組み合わせていくと、どんなベクトルが作れるだろうか? 逆に、複合的に表されたベクトルは、単純なベクトルに分解することができるだろうか? これが、線形代数学の基本的な考え方です。
線形代数学で最初に扱うことの多い「行列」は、ある意味で線形結合を略記したものです。
例えば、\(a=(a_1,a_2),b=(b_1,b_2)\)として、その線形結合は
\[\begin{aligned} x_1a+x_2b &= \begin{pmatrix} x_1 a_1 +x_2b_1\\x_1a_2+x_2b_2\end{pmatrix}\\&=\begin{pmatrix} a_1&b_1\\a_2&b_2\end{pmatrix}\begin{pmatrix} x_1\\ x_2\end{pmatrix} \end{aligned}\]
と表せます。この性質から、ベクトルは列ベクトル(縦ベクトル)を標準とすることが多いです。すると、\(A=\begin{pmatrix} a &b \end{pmatrix}\)と行列をベクトルを並べた対象として表記できます。
逆に言えば、行列\(A=\begin{pmatrix} a &b \end{pmatrix}\)は、ベクトル\(x=(x_1,x_2)\)を、\(a,b\)の線形結合\(Ax=x_1 a+x_2 b\)へ写すものです。
行列は、1次方程式(線形方程式)の定式化\(Ax=b\)にも使われます。その左辺\(Ax\)は、係数からなるベクトルの線形結合にほかなりません。このように、線形結合は線形代数学において基本的な対象なのです。
ベクトルの張る空間、線型部分空間
さて、線形結合によって表されるベクトルの集まりは、どんな対象になるのでしょうか?
例えば、\(\mathbb{R}^2\)において、\(x=(1,0),y=(2,0)\)とします。その線形結合\(c_1x +c_2y\)は、倍率\(c_1,c_2\)が変化したとき、どんなベクトルになりうるか。
一般に、ベクトルの有限個の集まり\(S\)の線形結合によって表されるベクトルの集合を、\(S\)の張る(span)空間、または\(S\)が生成する(generate)空間と言い、\(\mathrm{span}(S)\)と書きます。
\(S=\{v_1,\dots,v_k\}\subset \mathbb{R}^N\)のときは、次のように定義されます。
\(\mathrm{span}(S):=\{v \in \mathbb{R}^N \mid \exists c_1,\dots,c_k \; v = c_1 v_1+ \cdots + c_k v_k\}\)
\(S_1=\{x,y\}\)ならば、\(\mathrm{span}(S_1):=\{z \in \mathbb{R}^2 \mid \exists c_1,c_2 \; z = c_1 x+ c_2 y\}\)です。成分を計算すれば、\(c_1x +c_2y=(c_1+2c_2,0)\)なので、第2成分がすべて0の直線となります。したがって、\(\mathrm{span}(S_1)=\{(x_1,0) \mid x_1 \in \mathbb{R}\}\)です。
別の例をあげてみましょう。\(S_2=\{(1,0),(2,2)\}\)とします。線形結合は\((c_1+2c_2,2c_2)\)です。これは\(\mathbb{R}^2\)のすべてのベクトルを表すと言えます。任意に\((x_1,x_2)\in \mathbb{R}^2\)を取ると、
\[ \begin{aligned}(x_1,x_2)=(x_1-x_2)(1,0)+\frac{x_2}{2}(2,2)\end{aligned} \]
と表せるので。よって、\(\mathrm{span}(S_2)=\mathbb{R}^2\)です。
2つのベクトルによって張られる空間でも、一方は1次元的、もう一方は2次元的という違いが生まれましたね。
しかしそのどちらも、閉じた空間と呼ばれるに足る性質を持っています。
\(W\)を\(\mathbb{R}^N\)の部分集合として、任意の\(v,w \in W,c\in \mathbb{R}\)に対して\(v+w\in W, cv \in W\)となるとき、\(W\)を\(\mathbb{R}^N\)の線型部分空間(linear subspace)と言います。その要素を使って線形結合を作るという操作について閉じた集合が、部分空間です。
\(\mathrm{span}(S_1)=\{(x_1,0) \mid x_1 \in \mathbb{R}\}\)は、\(\mathbb{R}^2\)の部分空間です。その任意の要素は、\(v=(v_1,0),w=(w_1,0)\)と表せます。したがって、\(v+w=(v_1+w_1,0)\in \mathrm{span}(S_1)\)で、\(cv=(cv_1,0)\in \mathrm{span}(S_1)\)が成立するので。
同様にして、\(\mathrm{span}(S_2)=\mathbb{R}^2\)は、\(\mathbb{R}^2\)の部分空間です。一般に、\(\mathbb{R}^N\)自身は\(\mathbb{R}^N\)の部分空間です。
ベクトルの張る空間\(\mathrm{span}(S)\)は、\(S\)が何であっても、線型部分空間となります(確かめてみてください)。なので、\(\mathrm{span}(S)\)を張る空間と呼んだわけです。また、\(\mathrm{span}(S)\)は\(S\)を含む最小の部分空間です。
以降の議論では、張るベクトルはすべて0ベクトルでない\(v_i \neq 0\)と仮定しています。\(0\)を加えても張る空間は変わりませんし、カウントする意味がないからです。
すべての部分集合が、線形部分空間となるわけではありません。
\(W:=\{(x_1,x_1^2) \in \mathbb{R}^2 \mid x_1 \in \mathbb{R}^2\}\)、つまり\(f(x)=x^2\)のグラフとしてみましょう。\(W\subset \mathbb{R}^2\)ではありますが、線形部分空間ではありません。なぜなら、\((1,1)\in W\)ですが、そのスカラー倍は\(2(1,1)=(2,2)\notin W\)だからです。つまり、この\(W\)は「非線形」な集合と言えます。(ただし、\(W\)は線形空間を曲げた対象、多様体として捉えられます)
線型部分空間の定義\(v+w\in W, cv \in W\)は、そこに属するベクトルを足し合わせたり伸ばしたりしても「外側」に出ないことを意味します。つまり、線型部分空間は、直線や平面、立体といった直線的な形を持っているわけです。
また、行列は線形部分空間を線型部分空間へと移します。
一般に、行列はその定義から、「線形結合を線形結合へ写す」性質を持っています。
\[ \begin{aligned}A(c_1x+c_2 y)= c_1(Ax)+c_2(Ay)\end{aligned} \]
このような性質を持った写像(関数)を、線形写像(linear map)、線形変換(linear transformation)、一次変換と呼びます。
行列\(A\)によって線型部分空間\(W\)から移されるベクトルの集合を、\(A\)の像(image)、または値域(range)と言い、\(A(W)\)と書きます。\(A\)が\(n\times n\)の行列ならば、\( A(W)=\{v \in \mathbb{R}^N \mid \exists w\in W \; v=Aw\}\)です。
\( A(W)\)は、必ず線型部分空間です(確かめてみてください)。例えば、
\[A = \begin{pmatrix} 1&2\\ 0&0 \end{pmatrix}\]
ならば、\(A(\mathbb{R}^2)=\{(x_1,0) \mid x_1 \in \mathbb{R}\}\)で、部分空間ですね(さきほどの\(\mathrm{span}(S_1)\)に等しい)。(この\(A\)は2次元的な空間を、1次元へ潰しています。これはフルランク2ではなく、ランクが1つ落ちていることを表すものです。)
空間の次元、線形従属、線形独立、基底
これまで見てきたように、線形部分空間にはその広がり方の違いがあることがあります。
\(S_1=\{(1,0),(2,0)\}\)の張る空間\(\mathrm{span}(S_1)\)は直線で、\(S_2=\{(1,0),(2,2)\}\)の張る空間\(\mathrm{span}(S_2)\)は平面です。これらを区別するのが、線形空間の次元という考え方です。
共に2つのベクトルで張られる空間ですが、これらは何が違うのでしょうか?
\(\mathrm{span}(S_1)\)は2つのベクトルにより張られていますが、機能しているのは実質一種類であることに気づきます。なぜならば、\((2,0)=2(1,0)\)と、\((2,0)\)は\((1,0)\)のスカラー倍で表せているのです。2つのベクトルの線形結合であっても、1つにまとめられてしまうわけですね。このようなベクトルの集まりを、線形従属(linearly dependent)、一次従属と言います。
より一般に、\(S=\{v_1,\dots,v_k\}\)が線形従属であるとは、あるベクトル\(v_i\)が他のベクトルの線形結合で表せることです。これは\(0\)でない係数\(c_i\)で、\(c_1 v_1+\cdots+ c_k v_k=0\)なるものが存在するとも言い換えられますね(\(v_i\)以外を移項し、\(c_i\)で割る)。
一方で、\(S_2=\{(1,0),(2,2)\}\)は2つのベクトルが空間の生成に機能しています。これらは線形従属ではありません。\(c_1(1,0)+c_2(2,2)=0\)と仮定すると、必然的に\(c_1=c_2=0\)となり、あるベクトルを他のベクトルの線形結合で表せません。このような関係を、線形独立(linearly independent)、一次独立と言います。
より一般に、\(S=\{v_1,\dots,v_k\}\)が線形独立であるとは、そのすべてのベクトル\(v_i\)が他のベクトルの線形結合で表せないことです。これはもし\(c_1 v_1+\cdots+ c_k v_k=0\)ならば、\(c_1=\cdots=c_k=0\)となる、とも言い換えられます。
ここまで来ると、もう次元の定義はわかるでしょうか。重要なのは、線形独立なベクトルの個数です。
線形空間\(V\)において、線形独立であり、\(V\)を生成するような\(S=\{v_1,\dots,v_k\}\)を、\(V\)の基底(basis)と言います。そして\(V\)の基底の個数\(k\)を、\(V\)の次元(dimension)と言い、\(\dim V =k\)と書きます。(次元は、線形空間に応じて一意に定まります)
例えば、\(\mathrm{span}(S_1)=1\)です。基底としては、\((1,0)\)が選べます。1個のベクトルは線形独立であり、また、\(\mathrm{span}(S_1)\)の任意の要素は\((x_1,0)=x_1(1,0)\)と表せます。基底そのものは一意的に定まるわけではありません。例えば、\((4,0)\)も基底ですね。ただし、どのような基底を選んでも、その個数(=次元)はきちんと定まっています。
そして、\(\dim \mathrm{span}(S_2)=\dim \mathbb{R}^2=2\)です。線形独立であることは確かめましたし、空間を生成してもいます。
いくつかのベクトルによって、空間全体を張ることを考える。そのとき、余分なベクトル(線形従属)を排除し、線形独立なベクトルのみをカウントすることによって、次元を測ることができます。こうして見ても、次元というアイデアの根底にあるのは、線形結合であることは感じ取れるでしょうか。
行列(線形写像)は、線形空間の次元を落とさないことも、落とすこともあります。
\[A = \begin{pmatrix} 1&2\\ 0&0 \end{pmatrix}\]
ならば、\(A(\mathbb{R}^2)=\{(x_1,0) \mid x_1 \in \mathbb{R}\}\)なので、\(\dim A(\mathbb{R}^2)=1\)です。\(A\)の列ベクトルは線形従属になっています。このようなとき、\(A\)は正則ではないと言います。逆に、行列が正則なときは、像によって次元は保たれますし、またその列ベクトルが線形独立になります。
なんとなく、行列の変換としての側面、幾何学的なイメージが見られます。線形結合、そして次元というアイデアがあれば、行列は単なる数を並べたものではないことがわかりますね。
まとめ
実数空間:ベクトルには足し算、スカラー倍の2種類の基本的な演算がある
線形結合:いくつかのベクトルと基本演算の組み合わせによって表せるベクトル
ベクトルの張る空間:線形結合により表しうるベクトルの集まり
線型部分空間:和、スカラー倍について閉じたベクトルの集まり
空間の次元:空間を張るにあたって有効なベクトル(基底)の個数
線形代数学では、線形結合や行列によって線形的な関係を表し、その関係によって表される線形空間の広がり(次元)を調べます。
今回は2次元の例を紹介しましたが、3次元、4次元、\(n\)次元でも同様に議論できるでしょう。ぜひ単純なケースから操作やイメージを身に着け、スムーズに議論できるようになってみてください。
行列や固有値などについて学ぶときも、こうした幾何学的な、「線形的な」イメージを伴わせると、有機的に理解できると思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社
売り上げランキング: 121,346
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
述語論理、量子化とは:全称記号(∀)と存在記号(∃)、数学における例と否定