どうも、木村(@kimu3_slime)です。
今回は、線形代数の応用として、関数の「空間・基底・内積」を使ったフーリエ級数展開を紹介します。
フーリエ級数展開とは
まず、フーリエ級数展開とは何か、簡単に紹介しておきましょう。
18世紀の数学者・物理学者のジョゼフ・フーリエ(Fourier)は、固体の内部における熱伝導の時間発展について、すなわち熱伝導方程式を研究し、次のようなアイデアにたどり着きました。
任意の関数は、三角関数の無限和(フーリエ級数)として展開できる。
\[\begin{aligned} f(x)&=a_0 + a_1 \cos x + b_1 \sin x \\&+a_2 \cos 2x+ b_2 \sin 2x +\cdots \end{aligned} \]
「任意の関数」の意味合いは後に厳密化されていましたが、「三角関数に分解できる」というアイデアは正しく有効なもので、熱伝導方程式や波動方程式の解法、フーリエ変換など、数々の応用が生まれていきました。
僕たちが身近に感じる光や音、電磁波も、単純な波が組み合わさってできる波動現象で、どんな周波数の波がそれに含まれているかを、フーリエの理論は教えてくれます。近年では、電気信号による情報の送受信、いわゆる通信理論を通して、その恩恵に預かっていない人はいないでしょう。
関数の「空間・基底」とは
「任意の関数を、ある一部分の関数の集まり(三角関数)の和として表すことができる。」
これに似た表現を、線形代数学で聞いたことはないでしょうか。……そう、それは基底です。
2次元の空間に対して標準的な基底を使えば、任意のベクトルは\((x_1,x_2) = x_1(1,0) + x_2 (0,1)\)と表せます。
線形空間\(V\)と、有限個のベクトルの集まり\(\{v_i \}_{i=1} ^N\)があるとします。\(\{v_i \}_{i=1} ^N\)が線形独立であり、任意の\(x \in V\)がその線形結合\(x = a_1 v_1 +\cdots a_N v_N \)として表されるとき、\(\{v_i \}_{i=1} ^N\)を基底というのでした。基底の個数\(N\)が、次元と呼ばれるものです。
任意のベクトルは、基底を使った有限和として表せる。同じようなことを、関数に対して行うことはできないか? これがアイデアです。
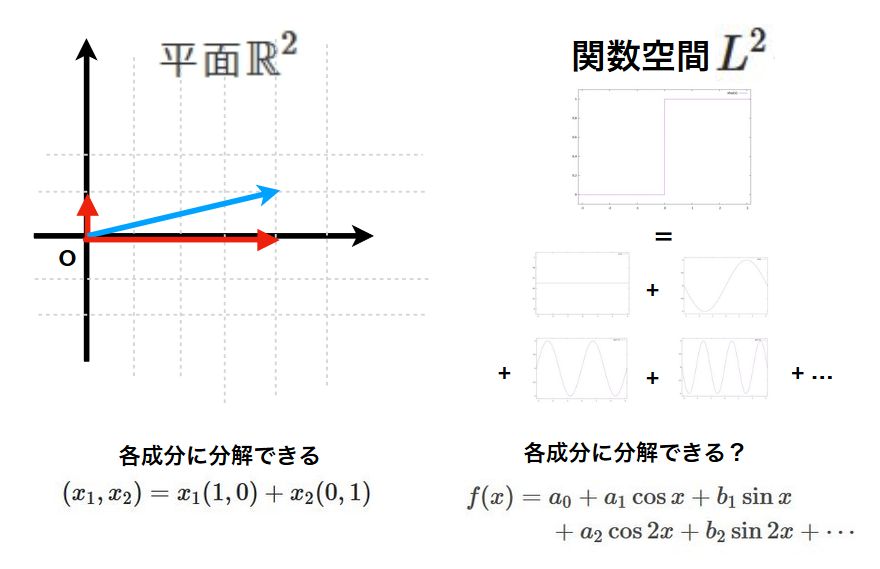
そこで、関数のなす空間、関数空間を考えましょう。関数空間にはいろいろなものがありますが、今回は二乗可積分関数(\(\int |f(x)|^2 dx <\infty\))のなす空間\(L^2\)を扱うことにします。
普通のベクトル(\(\mathbb{R} ^N\)や\(\mathbb{C} ^N\))では、ベクトル同士の和\(x+y\)や、スカラー倍\(c x\)と呼ばれる操作が可能でした。
関数に対しても、普通のベクトルと同じような操作ができます。確かに、\((f+g)(x) := f(x) +g(x)\)、\((c f)(x) := c f(x) \)と定めることにより、和とスカラー倍\(f+g,cf \in L^2\)が定まるので、\(L^2\)は線形空間と考えられます。(本当はもう少し細かい定義のチェックが必要ですが、省略)
では、関数空間が線形空間であるならば、任意の関数は有限和として表せるのか。そうはうまくいきません。
線形代数学では、通常考える空間を、有限次元のものに制限しています。しかし\(L^2\)のような関数空間は一般に、有限個の基底が存在しない、すなわち無限次元となるのです。
だからといって、関数の展開そのものを諦めることはありません。有限和ではなく、無限和としてうまく表すことはできないでしょうか。そこで視点を基底の角度、「内積」に移してみましょう。
内積と正規直交基底
有限次元のベクトルでは、その長さ(大きさ)や、2つのベクトルのなす角度を測ることができました。\(x,y \in \mathbb{R}^N\)として、
\[ \begin{aligned}\langle x, y\rangle := \sum _{i=1}^N x_i y_i ,\quad \|x \| :=\sqrt{\langle x, x\rangle }\end{aligned} \]
をそれぞれ、\(x,y\)の内積、\(x\)のノルムというのでした。ノルムはベクトルの長さの一般化です。
\(x,y\)のなす角度を\(\theta\)とすると、\(\langle x, y\rangle =\|x\| \|y\| \cos \theta\)という性質が成り立っています。そのため、\(\langle x, y\rangle= 0\)のとき、なす角度は\(90^{\circ}\)で、直交しているわけです。
そして、互いに直交するベクトルの集まり\(\{v_i \}_{i=1} ^n\)は、線形独立であることが知られています(逆は一般には成り立たない)。つまり、ベクトルの直交性は線形独立性より強い条件です。
\(\mathbb{R}^N\)においては、第\(i\)成分が1である標準基底\(\{e_i \}_{i=1} ^N\)が存在します。これは互いに直交していて、ノルムが1なので、正規直交基底とも呼ばれます。
正規直交基底を使えば、\(x= \sum _{i=1}^N \langle x, e_i\rangle e_i \)と表せます。内積\(\langle x, e_i\rangle \)は、\(x\)の\(e_i\)方向の大きさを取り出したものと見れますね。
逆に、関数空間\(L^2\)に「内積」が定まって、関数の無限列\(\{\phi_i\}_{i=1} ^{\infty}\)が、
- \(f= \sum _{i=1}^\infty \langle f, \phi_i\rangle \phi_i \) (完全性)
- 互いに直交していて(内積が\(0\))
- ノルムが1
を満たすようなものがあったらどうでしょうか。これを満たす\(\{\phi_i\}_i ^{\infty}\)を、正規直交基底(orthonormal basis)、または完全正規直交系(complete orthogonal normal series, CONS)と呼びます。
ここでは関数というベクトルの「無限和」を使って表現することを考えているので、上で紹介した基底(代数的基底)とは別の概念であることに注意してください。
問題は、\(L^2\)の内積とは何かということです。関数の定義域は\((-\pi,\pi)\)で、実数値関数としましょう。
\[ \begin{aligned} \langle f,g \rangle := \int _{-\pi} ^{\pi} f(x)g(x) dx,\quad \|f\| := \sqrt{\langle f,f \rangle} \end{aligned} \]
このように定めると、双線形性、対称性、非負性といった性質が、積分の性質によって満たされ、内積であることが言えます。\( \mathbb{R}^n \)の内積と見比べると、\(\sum \to \int\)となったもので、形としては似ていますね。
三角関数列は関数空間の直交基底
こうして関数の内積を考えられるようになりました。
実は、関数空間\(L^2\)には完全正規直交基底が存在することが知られています。それは、\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{\infty}\)という三角関数列(を正規化したもの)です。
つまり、任意の\(f\in L^2 \)は
\[ \begin{aligned}f(x)= a_0 +\sum _{k=1}^\infty (a_k \cos kx + b_k \sin x) \end{aligned} \]
\[ \begin{aligned}a_0= \frac{1}{2\pi } \langle f, 1\rangle ,\quad a_k =\frac{1}{\pi } \langle f, \cos kx\rangle,\quad b_k =\frac{1}{\pi } \langle f, \sin kx \rangle\end{aligned} \]
と展開されるのです。これがフーリエ級数展開ですね。
\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{\infty}\)が任意の関数を表せるという性質(完全性)は、証明が手間がかかるため省略します(黒田「関数解析」など参照)。ただし、これらが直交していることは、微積分を知っていれば簡単に見て取れます。例えば、
\[\begin{aligned} \langle \cos x, \sin x \rangle &= \int_{-\pi}^{\pi} \cos x \sin x\, dx \\ &= \int_{-\pi}^{\pi} \frac{1}{2} \sin 2x \,dx \\ &= [-\frac{1}{4} \cos 2x ]_{-\pi} ^{\pi}\\ &= 0\end{aligned} \]
です。いわゆる三角関数の加法定理を使えば、他の三角関数\(\cos 0x, \cos kx, \sin kx\)も互いに直交していることがわかります。積をひとつの三角関数にまとめたとき、\(\cos nx\)と偶関数になり積分が消えるか、\(\sin nx\)と端点\(x=-\pi, \pi\)で値が消えるかですね。
試しに、次の角張った関数(矩形波)をフーリエ級数展開し、グラフで表してみましょう。
\[ \begin{aligned} f(x)= \begin{cases} 0 & (-\pi <x <0 )\\1 & (0<x <\pi)\end{cases} \end{aligned} \]
計算は省略しますが、\(\cos \)の成分はすべて消え、\(\sin\)は\(k\)が奇数のもののみ残ります。
\[ \begin{aligned}f(x)= \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x + \frac{2}{5\pi} \sin 5x+ \cdots\end{aligned} \]
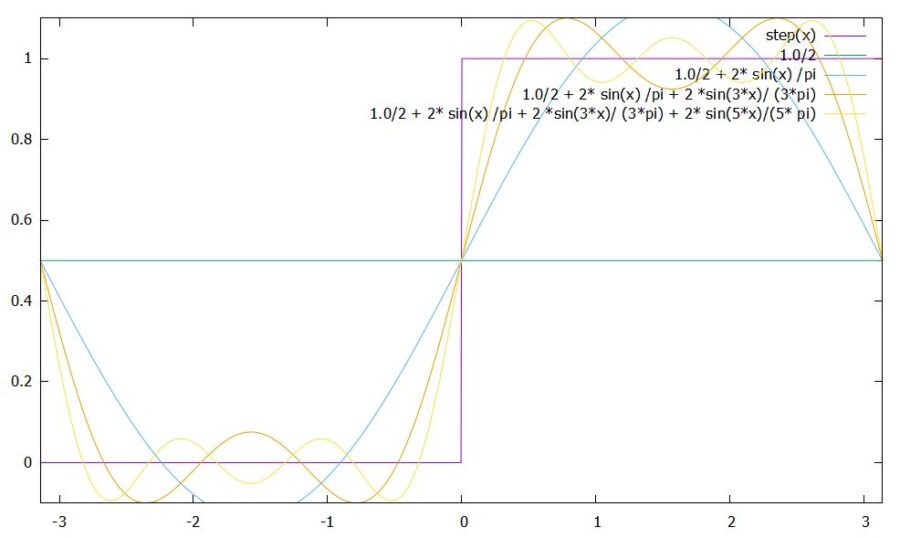
最初は\(\frac{1}{2}\)という定数関数で近似する。続いて、そこに\(\sin x\)の成分を加える。さらに、より起伏の数が多い\(\sin 3x\)の成分を加えることで、\(\sin x\)の山が平らになるようにしていく。……この繰り返しにより、グラフは限りなくもとの角張った関数に近づいていきます。
もとの関数\(f\)と三角関数の内積(これはフーリエ係数と呼ばれる)
\[ \begin{aligned}a_0= \frac{1}{2\pi } \langle f, 1\rangle ,\quad a_k =\frac{1}{\pi } \langle f, \cos kx\rangle,\quad b_k =\frac{1}{\pi } \langle f, \sin kx \rangle\end{aligned} \]
は、もとの関数のうち、どれだけの強さ(振幅)でその三角関数の成分が含まれているかを示すものです。今回の例ならば、\(\cos \)成分はすべて\(0\)で、\(\sin x\)成分は\( \frac{2}{\pi}\)、\(\sin 2x\)成分は\(0\)、\(\sin 3x\)成分は\( \frac{2}{3\pi} \)となっています。
ここまで、線形代数学(有限次元)で知っていたことから出発して、関数空間\(L^2\)の内積、直交基底、フーリエ級数展開を紹介してきました。
関数空間\(L^2\)や、関数の無限和の意味は、厳密にはルベーグ積分の言葉を使って書かれています。詳しく知りたい人は、ルベーグ積分論を勉強してみてください。
また、今回は三角関数列が直交系であることを紹介しましたが、エルミート多項式やルジャンドル多項式のように、多項式関数の直交系も知られています。これらは微分方程式や、離散的なデータを曲線でつなぐカーブフィッティング(曲線回帰)に応用されています。
この記事を通して、線形代数学の抽象的な部分が役に立つのが見れたでしょうか。無限次元の関数空間を扱う分野は、関数解析学として知られています。フーリエ解析は広く社会に応用されるものですが、その基礎として線形代数学があることを感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社
売り上げランキング: 168,641
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方