どうも、木村(@kimu3_slime)です。
高校の物理学で習う、惑星の運動に関するケプラーの法則
第一法則:惑星は、太陽をひとつの焦点とする楕円軌道を描く
第二法則:惑星と太陽とを結ぶ線分が単位時間に描く面積(面積速度)は、一定である。
第三法則:惑星の公転周期の2乗は、軌道長半径の3乗に比例する。
を、微積分と運動方程式・万有引力の法則によって導出・証明してみましょう。
ケプラーの法則は経験的に示唆されたものでしたが、微積分・万有引力の法則により、理論的に説明されたのです。万有引力、ニュートン力学そのもののパワー・信頼性を示した例と言えるのではないでしょうか。計算は少し長くなりますが、ぜひついてきてください。
ケプラーの法則の微積分による導出・証明
前提知識、仮定
3次元の空間を考え、太陽を原点の位置にあるとし、時刻\(t\)における惑星の位置を\(x(t)=(x_1(t),x_2(t),x_3(t))\)とします。それぞれの質量を\(M,m\)とします。
太陽と惑星は十分離れていて、それぞれ質点とみなせるとして、惑星の運動は運動方程式に従います。
\[ \begin{aligned}ma= f\end{aligned} \]
太陽と惑星に働く力は\(f\)は、万有引力の法則によって
\[ \begin{aligned}f= -G Mm \frac{x}{|x|^3}\end{aligned} \]
と表されるのでした(太陽による引力は十分大きいものとし、他の惑星による引力を無視しています)。ここで\(G\)は万有引力定数と呼ばれる定数です。
計算の簡略化のため、定数を\(k:= GM>0\)とおくと、
\[ \begin{aligned}a= -k \frac{x}{|x|^3}\end{aligned} \]
となりました。
運動がある平面上のものとなること
まず、ケプラーの第一法則、第二法則の前提となっている、運動がある平面上のものとなることを示しましょう。
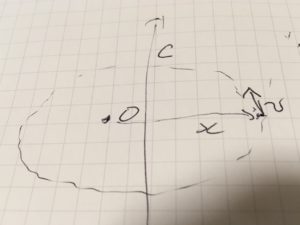
まず、運動方程式から\(x\times v=c\)となる時間に依存しないベクトル\(c\)が存在することが示せます。(\(\times\)はベクトルの外積、ベクトル積)
\[\begin{aligned} \frac{d(x\times v)}{dt} &= x \times \frac{dv}{dt} \\ &= x\times a \\ &= -k \frac{1}{|x|^3} x\times x \\ &=0 \end{aligned} \]
よって、\(x\times v=c\)を満たすベクトル\(c\)が存在します。
外積の定義より、常に\(x(t),c\)は直交します。すなわち、運動は\(c\)に直交する平面上にある、と言えました。
(角運動量\(L:=x\times p=x\times(mv)\)が一定となることは、角運動量保存の法則と呼ばれます。万有引力では角運動量が保存されますが、より一般に、大きさが原点からの距離のみに依存する力\(f=-f(|x|)\frac{x}{|x|}\)、中心力だけが働く運動でも角運動量は保存されます。)
第二法則
まず、ケプラーの第二法則、面積速度一定の法則を示しましょう。
\(S(t)\)を惑星\(x(t)\)と太陽\(0\)とを結ぶ線分が、時刻\(0\to t\)で描く面積とします。時間\(t\)から\(t+h\)までに描く面積\(S(t+h)-S(t) \)を考えましょう。
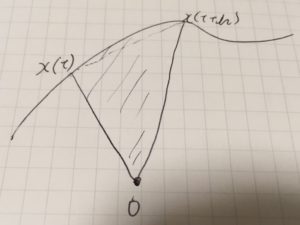
\(h\)が小さいとき、\(S(t+h)-S(t)\)はベクトル\(x(t),x(t+h)\)のなす三角形の面積
\[ \begin{aligned} \frac{1}{2} x(t) \times x(t+h)\end{aligned} \]
に近似されます。また、扇形の面積から三角形部分を除いた面積は、\(h\to 0\)ののとき非常に小さいので、
\[ \begin{aligned}S(t+h)-S(t) = \frac{1}{2} x(t) \times x(t+h) + o(h) \end{aligned} \]
です(\(o\)はランダウ記号)。極限計算のため、\(x(t+h)\)を\(h\)についてテイラー展開すると、
\[ \begin{aligned}x(t+h) = x(t)+ v(t) h +o(h),\quad(h\to 0)\end{aligned} \]
です。したがって、
\[ \begin{aligned} \frac{dS}{dt} & =\lim _{h\to 0} \frac{S(t+h)-S(t)}{h} \\ &= \lim _{h\to 0} \frac{ x(t) \times x(t+h)}{2h}\\ &= \lim _{h\to 0} \frac{ x(t) \times (x(t) +v(t)h)}{2h} \\ &= \lim _{h\to 0} \frac{ x(t) \times x(t) }{2h}+ \frac{x(t)\times v(t)}{2} \\ &= \frac{x(t)\times v(t)}{2}\end{aligned} \]
と角運動量の定数倍に等しいことがわかります。よって、先程の計算(角運動量保存則)により、\(\frac{dS}{dt}= \frac{1}{2} c=\frac{L}{2m}\)で時間によらず一定です。
運動方程式の極座標表示
第一法則、楕円軌道となることを示すためには、微分方程式をある程度解く必要があります。
運動は平面上のものであることは示せたので、2次元の極座標\((r,\theta)\)を使って、運動方程式を書き直しましょう。
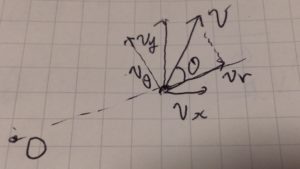
元の直交座標を\(x,y\)として、\(x=r\cos \theta,y=r \sin \theta\)です。速度、加速度を計算すると
\[ \begin{aligned}\dot{x}= \dot{r}\cos \theta – r\dot {\theta} \sin \theta\end{aligned} \]
\[ \begin{aligned}\dot{y}= \dot{r}\sin \theta + r\dot {\theta} \cos \theta\end{aligned} \]
\[ \begin{aligned}\ddot{x}= (\ddot{r}- r \dot{\theta} ^2)\cos \theta -( r\ddot {\theta}+2 \dot{r}\dot{\theta} )\sin \theta\end{aligned} \]
\[ \begin{aligned}\ddot{y}= (\ddot{r}- r \dot{\theta} ^2)\sin \theta + ( r\ddot {\theta}+2 \dot{r}\dot{\theta} )\cos \theta\end{aligned} \]
です。ただしここでドットは時間微分を表します。
\[ \begin{aligned}\begin{pmatrix}\ddot{x} \\ \ddot{y} \end{pmatrix} = \begin{pmatrix}\cos \theta & – \sin \theta\\\sin \theta & \cos \theta\end{pmatrix} \begin{pmatrix} \ddot{r}- r \dot{\theta} ^2 \\ r\ddot {\theta}+2 \dot{r}\dot{\theta} \end{pmatrix} \end{aligned} \]
極座標は直交座標を\(\theta\)だけ回転させたものなので、極座標における\(r,\theta\)の加速度は\(\ddot{r}- r \dot{\theta} ^2,r\ddot {\theta}+2 \dot{r}\dot{\theta} \)となります。
また、万有引力の\(r,\theta\)成分はそれぞれ\(-GMm\frac{1}{r^2},0\)なので、極座標における運動方程式は
\[ \begin{aligned}\ddot{r}- r \dot{\theta} ^2= -k\frac{1}{r^2}\end{aligned} \]
\[ \begin{aligned}r\ddot {\theta}+2 \dot{r}\dot{\theta}=0 \end{aligned} \]
と得られました(両辺\(m\)で割った)。
第一法則
もし\(r,\theta\)が
\[ \begin{aligned}r= \frac{\ell}{1+\varepsilon \cos \theta}\end{aligned} \]
という形に表せたら、運動は二次曲線、特に楕円軌道となることが言えます。
この形を導くため、\(r(\theta)\)と考え、極座標の運動方程式を、\(r,\theta\)のみに関する微分方程式に単純化していきましょう。
まず、\(\dot(\theta)\)は\(r\)のみによって表せます。\(\theta\)の運動方程式より、
\[\begin{aligned} \frac{d}{dt}(r^2 \dot{\theta}) &= 2 r \dot{r}\dot{\theta}+r^2 \ddot{\theta}\\ &= r(2\dot{r}\dot{\theta}+r\ddot{\theta}) &= 0\end{aligned} \]
なので、\(r^2 \dot{\theta}=h\)は定数です。つまり、\( \dot{\theta} = \frac{h}{r^2}\)です。
また、\(\dot{r},\ddot{r}\)から\(t\)を消していきましょう。
\[\begin{aligned} \dot{r}&= \frac{dr}{d\theta} \dot{\theta}\\ &= \frac{h}{r^2}\frac{dr}{d\theta} \\ &= -h \frac{du}{d\theta} \end{aligned} \]
です。ただし、\(u=\frac{1}{r}\)。さらに、
\[ \begin{aligned} \ddot{r}&= -h \frac{d^2 u}{d\theta^2} \dot{\theta} \\&=- \frac{h^2}{r^2}\frac{d^2 u}{d\theta^2} \\ \end{aligned} \]
です。よって、以上の計算を\(r\)の運動方程式に代入すると
\[ \begin{aligned}- \frac{h^2}{r^2}\frac{d^2 u}{d\theta^2} – \frac{h^2}{r^3}= – k \frac{1}{r^2}\end{aligned} \]
\[ \begin{aligned}\frac{d^2 u}{d\theta^2} = -u+ \frac{k}{h^2}\end{aligned} \]
です。この2階線形常微分方程式は簡単に解くことができて(単振動)、
\[ \begin{aligned}u(\theta) = A \cos \theta +B\sin \theta+ \frac{k}{h^2}\end{aligned} \]
です(\(A,B\)は定数)。定数を取り直して、
\[ \begin{aligned}u(\theta) = A \cos (\theta – \theta_0) + \frac{k}{h^2}\end{aligned} \]
とまとめられます(\(A,\theta _0\)は定数、かつ\(A\geq 0 \))。よって、
\[\begin{aligned} r&=\frac{1}{u}\\ &= \frac{\frac{h^2}{k}}{1+\frac{h^2 A}{ k} \cos (\theta – \theta_0)} \\&= \frac{\ell}{1+\varepsilon \cos (\theta – \theta_0)} \end{aligned} \]
ただし、\(\ell:=\frac{h^2}{k}\)、\(\varepsilon :=\frac{h^2 A}{ k}\geq 0\)です。
これは二次曲線(楕円、放物線、双曲線)の極座標による表示で、\(\varepsilon\)は離心率と呼ばれます。
\(\varepsilon\)の値は初期条件によって決まりますが、今回考えている惑星は、放物線、双曲線のように、無限に離れていってしまうものを考えていません。なので、楕円曲線に従います。これで第二法則が示せました。
第三法則
第三法則を示しましょう。惑星の公転周期を\(T\)、楕円の長半径、短半径を\(a,b\)とすると、\(T^2\)が\(a^3\)に比例するという法則です。
\(T\)は、楕円の面積を面積速度で割ったものとして求められます。
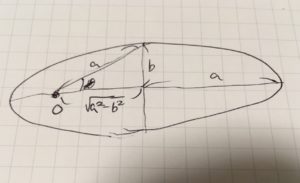
楕円の面積は\(\pi a,b\)です。離心率と長半径、短半径の関係\(\varepsilon =\frac{\sqrt{a^2-b^2}}{a}\)、\(\ell = \frac{b^2}{a}\)より、長半径は
\[ \begin{aligned}b= a \sqrt{1-\varepsilon^2} =\sqrt{a \ell}= h \sqrt{\frac{a}{k}}\end{aligned} \]
です。また、面積速度は\(dS/dt=\frac{x(t)\times v(t)}{2}\)でしたが、これは極座標を使って表すと
\[ \begin{aligned}|x\times v|= r v_\theta = r^2\dot{\theta}=h\end{aligned} \]
となります。
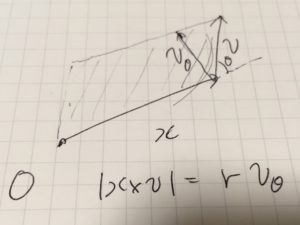
よって、公転周期\(T\)は
\[ \begin{aligned}T=\frac{\pi ab}{h/2} = 2\pi \sqrt{\frac{a^3}{k}}\end{aligned} \]
となり、\(T^2\)は\(a^3\)に比例することが言えました。
まとめ
- 万有引力(中心力)の仮定から、運動が平面上になり、角運動量保存が言える
- 第二法則、面積速度一定は、角運動量保存からのそのままの帰結。
- 第一法則、楕円軌道は、運動方程式と逆二乗則から計算によって導かれる。極座標によって整理する。
- 第三法則は、第一、第二法則の組み合わせ。
ケプラーの法則は、天体の運動に関する経験的な法則でした。しかしそれは、微積分、そしてニュートン力学によって、理論的に導出できるものとなりました。つまり天体の運動の基礎を説明するのに、微積分・ニュートン力学が有効であることを示した重要な例と言えると思います。
数学的なテクニックとしてだけ微積分を見るのでなく、天体の運動について調べることもできると思えば、微積分を学ぶモチベーションも出てくるのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。