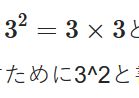どうも、木村(@kimu3_slime)です。
統計学による推測では、調べたい対象(母集団)からサンプルを取り出し、そのサンプルを調べることで母集団の性質を予測します。
一部分を取り出しただけなのに、どうして全体を知ることができるのか? それは、確率論的な原理によるものです。
その原理には、大数の法則と中心極限定理がありますが、今回は大数の法則を紹介します。
大数の法則とは:ざっくり言えば
(表裏が平等に出る)コインを何回も投げ続ける状況を考えましょう。
表裏表裏裏裏……と出方がばらつくことは当然ありますよね。しかし、これを100回、1000回、10000回と続けるとしたらどうでしょう? 全体で見れば、表と裏の出る割合が同じになっていく気がしませんか?
表=1、裏=0と事象を数値化して、\(n\)回目の試行で出る値を\(X_n\)としましょう。試行の平均\(M_n:=\frac{X_1+\cdots+X_n}{n}\)は、\(n\)が大きいほど\(1/2\)に近づいていくのではないでしょうか。
このように、試行回数が増えれば増えるほど、試行の平均が期待値(理論値)に近づいていく現象は、大数の法則(law of large numbers)と呼ばれます。
これがもっともらしいかどうか、シミュレーションで調べてみましょう。
以下、Pythonによるコード例と、\(n=5,100,1000,10000\)の結果のグラフです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | import random import numpy as np import matplotlib.pyplot as plt list1, mean1 = [], [] #リストにデータを格納していく n = 1000 #試行回数の指定 for i in range(n): x = random.randint(0, 1) #乱数の生成。今回は、0または1の値を返す。 list1.append(x) #出目の結果を記録していく mean1.append(np.mean(list1)) #リストの平均を取る #結果の視覚化 plt.plot(range(n),mean1) plt.ylim(0,1) plt.show() |
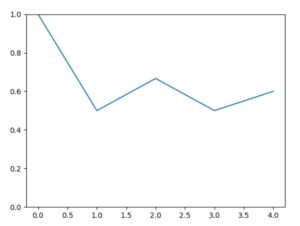
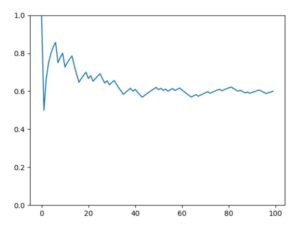
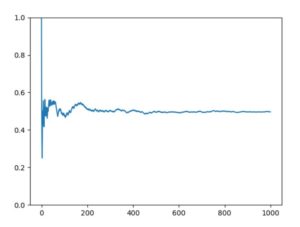
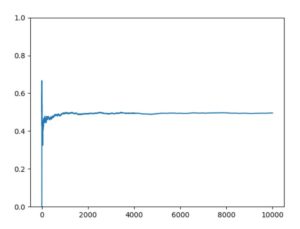
\(n\)が小さいときは、出目の平均にブレがあり、最終的には0.6程度です。しかしながら\(n\)が大きくなるにつれ、期待値である\(1/2=0.5\)からほぼぶれなくなっていることが確認できます。つまり大数の法則は成立していそうです。
コイン投げやサイコロ投げは、確率論の言葉で言えば一様分布を考えていることになります。他の分布について大数の法則は成り立ちそうなのかどうか、気になります。
平均50・分散10のガウス分布、平均50のポアソン分布、\(\alpha=1,\beta=5\)のガンマ分布に従う乱数による10000回試行の平均値のグラフは、次のようになりました。
Pythonにおける乱数について:random — 擬似乱数を生成する – Pythonドキュメント
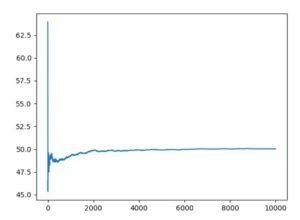
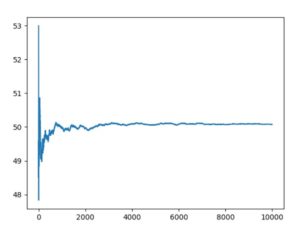
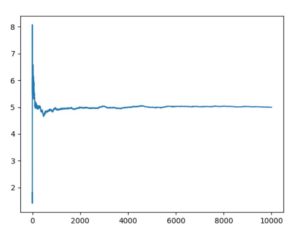
どれも最初はぶれがありますが、やがて平均に収束するように見えます。
確かに、種々の分布で大数の法則が成り立っているように見えることがわかりました。
しかしこれは単なる経験則ではなく、数学の定理として証明できることです。
大数の法則とは:数学的に
確率変数の族\(\{X_i\}_{i\in \mathbb{N}}\)を考えます。これらは独立で、同一の確率分布\(X\)に従うとする。
このとき、期待値と分散は同一になるので、\(E[X]:= E(X_i), V[X]= V(X_i)\)とおく。
確率変数の族の平均を\(M_n:=\frac{X_1+\cdots+X_n}{n}\)とする。
確率統計の基本用語については:Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう、確率・統計における用語「分布」について整理する
大数の弱法則
\(E[X^2]<\infty\)とする。
このとき、任意の\(\varepsilon >0\)に対し、
\[ \begin{aligned}\lim _{n\to\infty} P (|M_n – E[X]| \geq \varepsilon) = 0 \end{aligned} \]
この収束の条件を、確率変数の族\({M_n}\)は\(E[X]\)に確率収束(convergence in probability)すると言います。
大数の強法則
\(E[X^4]<\infty\)とする。
このとき、次の式が成立する。
\[ \begin{aligned}P (\lim _{n\to\infty} M_n = E[X] ) = 1 \end{aligned} \]
この収束の条件を、確率変数の族\({M_n}\)は\(E[X]\)に概収束する(almost sure convergence)と言います。
統計学的解釈
大数の法則を、統計学的に読み直してみましょう。
同一の分布に従う確率変数族\(\{X_i\}\)を考えることは、調べたい集団(母集団)\(X\)の設定に対応します。もし、別の分布に従うと仮定してしまったら、調査の対象がブレてしまうわけです。
ひとつひとつの確率変数\(X_i\)は、母集団から取り出してきたサンプルです。1回1回の試行、調査の結果とも言えます。
サンプルは、確率的なモデルとして設定された母集団分布から得られたと考えているわけです。そのうえで、サンプルから未知なる母集団分布の性質を引き出すのが、統計的な推測です。
確率変数族\(\{X_i\}\)が独立であることは、サンプルがランダムに取られてきたことを保証するもので、ランダムサンプリング(無作為抽出 random sampling)と呼ばれます。
以上の仮定の上で、大数の(弱)法則は何を意味するか。
任意の\(\varepsilon >0\)に対し、
\[ \begin{aligned}\lim _{n\to\infty} P (|M_n – E[X]| \geq \varepsilon) = 0 \end{aligned} \]
サンプルの平均\(M_n\)と母集団の平均\(E[X]\)が少しでも異なる確率は、サンプルサイズ\(n\)を十分大きくすれば限りなく0に近づいていく。
強法則は、サンプル平均の分布が\(n\to\infty\)で期待値に一致する確率は1である、と言っています。
つまり、母集団分布の期待値を知りたいならば、サンプルサイズを増やしたときのサンプル平均を見ればいい、それで推測ができる、というわけです。
チェビシェフの不等式
今回は、大数の弱法則のみ証明します。強法則の証明は、例えば熊谷「確率論」のp.24~を参照。
チェビシェフ(Chevyshev)の不等式は、大数の弱法則の証明の肝です。それ自体役立つものなので、詳しく紹介しましょう。
\(X\)を確率変数で\(E[X^2]<\infty\)を満たすものとする。このとき、任意の\(a>0\)に対し、
\[ \begin{aligned}P(|X| \geq a) \leq \frac{E[X^2]}{a^2}\end{aligned} \]
が成立する。
チェビシェフの不等式を証明しましょう。
\[\begin{aligned} P(|X|\geq a) &=\int_{\{|X|\geq a\}} 1 dP \\ &= \frac{1}{a^2} \int_{\{|X|\geq a\}} a^2 dP\\ & \leq \frac{1}{a^2}\int_{\{|X|\geq a\}} X^2 dP\\ & \leq \frac{1}{a^2} \int_\Omega X^2 dP\\ &= \frac{E[X^2]}{a^2}\end{aligned}\]
より一般に、\(f\)を非負で広義単調増加な関数で、\(E[|f(X)|]<\infty\)とするとき、
\[ \begin{aligned}P(|X| \geq a) \leq \frac{E[f(X)]}{f(a)}\end{aligned} \]
が成り立ちます。今回は\(f(a)=a^2\)だったというわけです。証明はほぼ同じ。
チェビシェフの不等式において\(X\)を\(X-E[X]\)と置き直せば、
\[ \begin{aligned}P(|X-E[X]| \geq a) \leq \frac{V[X]}{a^2}\end{aligned} \]
とも言えます。
これは統計学的に解釈しやすいです。
例えば、\(a=2\sqrt{V[X]}\)としてみます。
\[ \begin{aligned}P(|X-E[X]| \geq 2\sqrt{V[X]}) \leq \frac{1}{4}\end{aligned} \]
期待値から標準偏差\(\sqrt{V[X]}=\sigma\)にして2個分以上離れた値(\((x-2\sigma,x+2\sigma) \)の外側)を取る確率は、常に25%以下と言えるわけです。それだけ外れた値を取る確率は分布によっては25%より小さいかもしれませんが、どんな分布でも最大で25%以下と言えるのが強力です。
一般に、標準偏差\(n\)個分だけ離れた値を取る確率は\(1/n^2\)ですね。
例えば日本では台風が年間平均でおよそ20-30回ほど訪れますが、そんなとき、年50回来ることは考えにくいし、100回来るのはありえないと自信を持って言えるでしょう。これはチェビシェフの不等式的な考え方ーー平均から(分散を考慮して)大きく外れた値を取る確率は小さいだろうーーを使っていると言えますね。
大数の法則の証明
では、任意の\(\varepsilon >0\)に対し、
\[ \begin{aligned}\lim _{n\to\infty} P (|M_n – \mu| \geq \varepsilon) = 0 \end{aligned} \]
を示しましょう。
\(\varepsilon >0\)を任意のものとします。
仮定を満たしているのでチェビシェフの不等式が適用でき、
\[\begin{aligned}P(|M_n – E[X]| \geq \varepsilon) & \leq \frac{V[M_n]}{\varepsilon ^2} \\ &= \frac{V[X_1+\cdots +X_n]}{n^2 \varepsilon ^2} \\ &= \frac{nV[X]}{n^2 \varepsilon ^2}\\ & \to 0\quad (\mathrm{as}\; n\to \infty) \end{aligned}\]
と言えました。
大数の法則での仮定\(E[X^2]<\infty\)は、チェビシェフの不等式を利用するためのもの、つまり平均\(M_n\)の分散の存在を保証するものだったというわけです。
またチェビシェフの不等式を使った評価は、\(V[M_n]\)が\(1/n\)のオーダー\(O(1/n)\)であることを示しています。\(M_n\)の分散は\(n\)が大きいほど限りなく小さくできるので、値が期待値付近にしか残らない状況になる。つまり大数の法則の成立と言えます。
証明の過程で
\[V[X_1 +\cdots +X_n] = n V[X]\]
となる変形で、確率変数の族\(\{X_i\}_{i\in \mathbb{N}}\)が独立(同分布)であることを使っています。これも証明しておきましょう。
一般に、期待値の線形性から
\[\begin{aligned}V[X+Y] &= E [(X+Y-E[X+Y])^2]\\ &= E[(X-E[X])^2]+E[(Y-E[Y])^2]\\ & +2E[(X-E[X])(Y-E[Y])]\\ &= V[X]+V[Y] + 2\mathrm{Cov}(X,Y)\end{aligned}\]
となりますが、確率変数族の独立性の仮定から、\(E[XY]=E[X]E[Y]\)となるので、
\[\begin{aligned}\mathrm{Cov}(X,Y) &= E[(X-E[X])(Y-E[Y])]\\ &= E[XY-XE[Y]-YE[X]+E[XY]]\\ &= E[XY]-E[XY]-E[XY]+E[XY]\\ &=0 \end{aligned}\]
と共分散が0となり、分散の加法性が成立しています。
大数の法則の意義・まとめ
統計学において、サンプルが多いときは、サンプルの平均を母集団の真の平均として推定できる。このような統計的推測の基礎のひとつとして、大数の法則があります。
偶然に支配されるように見える現象でも、サンプルを増やせば期待値の値を取るようにコントロールできる。それは例えば保険に応用されているわけです。
参考:保険とは-大数の法則とリスクヘッジ – 浅野 晃の講義
もちろん、大数の法則の成立には仮定があります。ランダムサンプリングであること(確率変数族が独立同分布)、\(E[X^2]<\infty\)、つまり期待値が有限値として存在しなければなりません。
例えばコーシー分布では、期待値が発散します。Pythonの標準コーシー分布でシミュレーションを行うと、次のようになります。
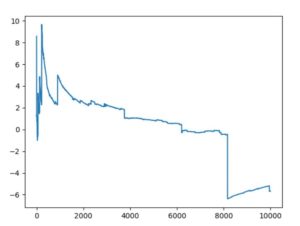
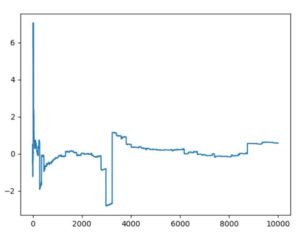
時折大きな変動を伴い、\(n=10000\)でもまるで一定の値に収束するようすが見られませんね。
また、大数の弱法則の証明には、「期待値から大きく外れた値を取る確率は小さい」というチェビシェフの不等式が使われているのでした。
ちなみにこのチェビシェフ、ロシアの数学者で、同じく数学者で確率論にも貢献したリアプノフやマルコフが弟子にいます。公理的確率論の基礎を作ったコルモゴロフもロシアの数学者で、ロシアには確率論の伝統があるのかもしれませんね。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう