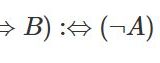論理に関するド・モルガンの法則を真偽値の計算（プログラミング）で確かめる

どうも、木村（@kimu3_slime）です。

論理に関するド・モルガンの法則を、真偽値の計算（Pythonを使ったプログラミング）で確かめる方法を紹介します。

ド・モルガンの法則

\(p,q\)を命題とする。このとき、

 \(\lnot (p \land q )= \lnot p \lor \lnot q \),\(\lnot (p \lor q )= \lnot p \land \lnot q \),

命題とは、真偽の定まった文のこと。そして、\(\lnot \)は「～でない」（否定）、\(\land \)は「かつ」（論理積）、\(\lor \)は「または」（論理和）を意味しています。

集合に関するド・モルガンの定理は

\( \overline{ A \cup B } = \overline{A} \cap \overline{B} \),\(\overline{ A \cap B } = \overline{A} \cup \overline{B}\)

です。今回はこちらではなく、論理に関するド・モルガンの法則を扱います。

これを確かめるPythonのコードを紹介します。

\(\lnot (p \land q )= \lnot p \lor \lnot q \)のみを扱いますが、もう一方も同様に示せます。

命題\(p,q\)が取る値はTrue（真）,False（偽）のいずれかです。このような値を真偽値、あるいはブール値（boolean value）と言います。

最初のforによって、\(p,q\)が真真、真偽、偽真、偽偽の場合を総当りしています。

そして、ド・モルガンの法則における左辺をl、右辺をrとして、両辺が同値か？（l == r ?）を出力するようにしました。

コードの実行結果は次の通り。

4通りすべてにおいて「l == r」がTrueなので、ド・モルガンの法則は正しいと言えます。

ド・モルガンの法則の一般化

さきほど紹介したのは、2つの命題に関するド・モルガンの法則でした。これは一般化することができます。

\(\lnot (p_1 \land p_2 \land p_3 )= \lnot p_1 \lor \lnot p_2 \lor \lnot p_3 \)

\(n \in \mathbb{N}\)として、

\(\lnot (p_1 \land \cdots \land p_n )= \lnot p_1 \lor \cdots \lor \lnot p_n \)

\(n=3 \)のとき、確かめるプログラムとその結果を紹介しましょう。繰り返しの処理に、 itertoolsを使いました。

すべて「l == r」がTrueであり、確かに正しいと言えました。

じつは、一般化されたド・モルガンの法則は、単に2つのド・モルガンの法則から証明することができます。

\(\begin{align*} \lnot \left( p_1\land p_2\land p_3 \right) & \Leftrightarrow \lnot \left( \left( p_1\land p_2\right) \land p_3 \right) \quad  \\ & \Leftrightarrow \lnot \left( p_1\land p_2\right) \lor \lnot p_3 \quad  \\ & \Leftrightarrow \left( \lnot p_1\lor \lnot p_2\right) \lor \lnot p_3 \\ & \Leftrightarrow \lnot p_1\lor \lnot p_2 \lor \lnot p_3 \quad  \end{align*}\)

ド・モルガンに法則は論理学における基本的な法則です。真偽値（ブール値）を調べれば、どんな命題に関しても正しいと言えます。一度チェックしてみると、論理に対する理解が深まるのではないでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。

論理と集合から始める数学の基礎

posted with amazlet at 19.09.06

嘉田 勝
日本評論社
売り上げランキング: 80,779

Amazon.co.jpで詳細を見る

 

こちらもおすすめ

「AならばB」のよくある誤解から学ぶ、論理学入門（対偶、逆、否定、真偽表）

集合論のはじまり、全称命題と存在命題、論理記号を知ろう

数学における証明とは、健全性、完全性とは？