どうも、木村(@kimu3_slime)です。
人間の人口や生物の個体数の増加は、微分方程式によって予測できる部分があります。
個体数が増えれば繁殖してさらに増えるという、単純に増加するモデルはマルサスモデル、指数関数的成長と呼ばれるものでした。
しかし、現実問題、人口や個体数は無限に増え続けるわけはありません。増え過ぎれば、食料が足りなくなったり、環境が悪くなったりして、繁殖率が下がるはずです。
今回は、こうした事情を取り入れた、ロジスティック方程式について紹介します。
ロジスティック方程式とは
\(u(t)\)を人口、もとい個体数を表す関数として、マルサスモデルは、次のような微分方程式でした。
\[ \begin{aligned}\frac{du}{dt}= u\end{aligned} \]
右辺に、\(u\)が大きいときにマイナスになる効果、\(-u^2\)を加えてみましょう。
\[ \begin{aligned}\frac{du}{dt}= ru(1 – \frac{u}{K})\end{aligned} \]
これがロジスティック方程式(logistic equation)です。\(r,K>0\)は定数で、その意味は後に紹介します。
この方程式は、積分によって解けることが知られています。
解は
\[ \begin{aligned}u(t)= \frac{K}{1+ C e^{-rt}}\end{aligned} \]
\[ \begin{aligned}C = \frac{K}{u(0) } -1\end{aligned} \]
となります。
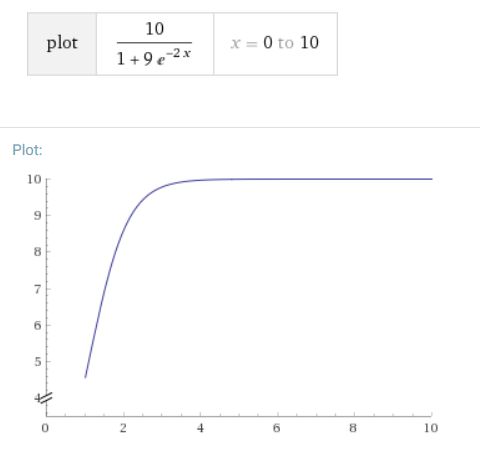
画像引用:Wolframalpha
\(u\)は最初グッと増加し、\(t\to \infty\)でゆるやかに\(K\)に収束します。
\(r\)は、個体数が少ないときの指数的な増殖の速さを表すもので、内的自然増加率(intrinsic rate of natural increase)と呼ばれます。
一方、\(K\)は環境収容力(carrying capacity)と呼ばれ、値が大きいほど最終的に住める個体数が増えるもの。
この解は、ロジスティック曲線と呼ばれる関数で、ベルギーの数学者:ヴェアフルスト(Verhulst 1804 – 1849)によって名付けられました。
ロジスティックの意味は、logistic(兵站の)よりはむしろ、対数曲線に似た(log-like)に近いと思われます。(参考:Logistic function – Wikipedia)
(ロジスティック曲線の特殊な場合として、シグモイド関数があります。シグモイド関数は、種々の応用があり、例えば学習モデル:ニューラルネットワークに使われることがあります。)
実際、ミジンコなどの微生物や小さな昆虫では、ロジスティック曲線に従った増え方をすることが知られています。
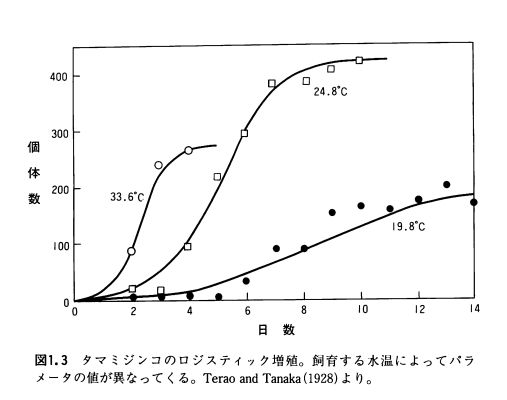
画像引用:巌佐 数理生物学入門―生物社会のダイナミックスを探る
環境によって、\(r,K\)の値を調節する必要があります。これらが、例えば温度、栄養、密度についてどんな影響を受けるか気になるものです。
ロジスティック方程式は、項をかけたり加えたりすることで、より詳細な記述ができます。例えば、\((u-a)\)をかけたり、\(\frac{u^2}{1+u^2}\)を引いたモデルを考えることがあります。
さらには、今回は1種の生物の増殖について考えましたが、2種の生物の個体数の増減のモデルを考えることができます。
それは被食者-捕食者モデル(ロトカ・ヴォルテラ方程式)と呼ばれるものですが、こちらもロジスティック方程式を基準にした増減を考えたもの。
個体数が少ないときには増加し、増加が一定に達したら増加率が下がっていく\(u(1-u)\) モデルは、単純でありながら基本的なモデルと言えるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
続編:食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?
共立出版
売り上げランキング: 346,705