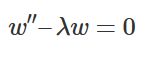どうも、木村(@kimu3_slime)です。
波と波が合わさってできる波は、元の波の高さを合わせたものとなることを、高校物理の時間に学びます。
これは、波の重ね合わせの原理と呼ばれる性質です。
このような重ね合わせの原理が成り立つのは、なぜなのでしょうか?
高校物理の一歩先の話として、波動方程式を簡単に紹介します。
波動方程式とは?
波動方程式(wave equation)とは、弦の振動や、音、光などの波がどう変化するかを説明する方程式です。
\(u\)を弦の振れ幅(変位)表す関数としましょう。時間\(t\)と場所\(x\)における変位を、\(u(x,t)\)として表します。
(縦の振れ幅:縦波を考えても、横の振れ幅:横波を考えても、同じ式になります。)
1次元の場合、次のような数式になります。
\[ \begin{aligned}\frac{\partial ^2 u}{\partial t^2} = \Delta u\end{aligned} \]
ここで、\( \Delta u = \frac{\partial ^2 u}{\partial x^2}\)です。
\(\frac{\partial u}{\partial t}\)は\(t\)に関する偏微分と呼ばれるもので、変数\(x\)を固定して\(t\)について微分したものです。偏微分を含む方程式は、一般に偏微分方程式と呼ばれます。
おおざっぱに言えば、「変位変化の加速度=波が凹の部分ではプラス、波が凸の部分ではマイナス」という規則です。
山になっている部分は消える方向に向かうわけですが、それに勢いがついていて、戻っていくときに逆向きの山ができ、また逆方向の変化に戻る……という現象を繰り返します。これはまさに波です。
波動方程式は、弦の微小区間に注目し、ニュートンの運動方程式を使って導くことができます。導出は例えば金子「偏微分方程式入門」を参照。
波動方程式が表せる現象では、弦が\(x\)軸となす角度が十分小さいという仮定があります。波長に比べて振幅が大きすぎるような波では、重ね合わせの原理が成立しなくなります。
さて、波動方程式では、重ね合わせの原理が成り立つことが数式によって簡単にわかります。
重ね合わせの原理とは、\(u_1,u_2\)を波動方程式の解とすると、\(u_1 + u_2\)、\(cu_1\)も波動方程式の解となる性質です。(\(c \in \mathbb{R}\)は定数)
つまり、二つの波を足し合わせたり、ある波の振幅(波の高さ)を伸ばしたりしたものもまた、波となる性質のことです。
計算してみましょう。
\[\begin{aligned} \frac{\partial ^2 (u_1 +u_2)}{\partial t^2} & = \frac{\partial ^2 u_1}{\partial t^2} + \frac{\partial ^2 u_2 }{\partial t^2} \\ & = \Delta u_1 + \Delta u_2 \\ & = \Delta (u_1 +u_2) \end{aligned}\]
\[\begin{aligned} \frac{\partial ^2 (cu_1)}{\partial t^2} & = c\frac{\partial ^2 u_1}{\partial t^2} \\& = c\Delta u_1 \\& = \Delta (cu_1 ) \end{aligned} \]
となるので、\(u_1 +u_2\)、\(cu_1\)も解となりました(和の微分は、微分の和となる:微分の線形性を用いています)。
一般に、解の重ね合わせの原理が成り立つような方程式を、線形方程式と呼びます。波動方程式は、線形の偏微分方程式です。
波動方程式の解の具体例を見てみましょう。
\(u(x,t)= \sin (t-x)\)とすると、
\[ \begin{aligned} \frac{\partial u }{\partial t } = \cos (t-x),\frac{\partial^2 u }{\partial t^2 }= – \sin (t-x) \end{aligned} \]
\[ \begin{aligned} \frac{\partial u }{\partial x } = -\cos (t-x),\frac{\partial^2 u }{\partial x^2 }= – \sin (t-x) \end{aligned} \]
なので、波動方程式を満たします。
三角波が時間とともに横方向へ進んでいく解で、進行波(progressive wave)と呼ばれるものです。
別の解を考えます。\(v(x,t)= \sin t \cdot \sin x\)とします。
\[ \begin{aligned} \frac{\partial v }{\partial t } = \cos t \sin x,\frac{\partial^2 v }{\partial t^2 }= – \sin t \sin x \end{aligned} \]
\[ \begin{aligned} \frac{\partial v }{\partial x } = \sin t \cos x,\frac{\partial^2 v }{\partial x^2 }= – \sin t \sin x \end{aligned} \]
三角波が横に動かず上下するもので、定常波(stationary wave)と呼ばれるものです。
全空間において、波動方程式の初期値問題\(u(x,0)=g,u_t (x,0)=h\)の解は、
\[ \begin{aligned}u(x,t)= \frac{1}{2} \{ g(x+t) +g(x-t)\} +\frac{1}{2} \int _{x-t} ^{x+t} h(y)dy\end{aligned} \]
と表されることが知られています。(ダランベールの公式 d´Alembert’s formula)
これは初期値関数が、時間とともに空間両側へ2つの進行波として分かれていくようすを表します。
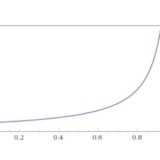
次の図は、\(u(x,0)=e^{-x^2},u_t (x,0)=0\)のときの解のようすです。
また、有界領域における(固定端の)境界値問題は、熱方程式と同様、変数分離とフーリエ級数によって解くことができます。このとき、解は定常波の重ね合わせとなります。
参考:熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)
波の重ね合わせの原理から出発し、波動方程式と、その典型的な解を紹介しました。
高校数学の微分積分、あるいは高校物理の熱や波動といった話は、発展すると熱方程式、波動方程式といった偏微分方程式の話につながってきます。ぜひ、少しずつ身近な現象に隠れた微分方程式のことを知ってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)