どうも、木村(@kimu3_slime)です。
ほんのわずかな初期状態の差にもかかわらず、やがて大きな違いを引き起こす現象、カオス現象。
そんなカオス現象のわかりやすい具体例を、視覚的に紹介していきます。
カオスについての予備知識はこちら:カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に
カオス現象の具体例
二重振り子
最もわかりやすくカオスを起こしているのが観察できる例が、二重振り子(double pendulum)です。
これは、単振り子(天井から歪まない糸で吊るされた重りによる振り子)を2つつなげたものとして理解できます。
実際に振り子を作るときは、振り子の連結部分の摩擦が少なくなるようにしないと、減衰が起きて止まってしまいます。
同様に、3つ振り子をつなげたものが3重振り子です。
次のシミュレーション動画では、ほとんど同じような初期状態(振り子の位置)が、ある瞬間を境に、一気にバラバラになる現象が見て取れます。
先日のカオス振り子動画を見て極端な場合を試してみたくなったので、3重振り子で高精度物理演算してみた。初期の振り子の角度を10の100乗(グーゴル)分の1ずつだけずらしたものを100個同時に再生。完全に一致してるように見えるけど、1分20秒くらいから「それ」がやってくる。 pic.twitter.com/a7E2OASIDe
— So Takamoto (JK) (@tkmtSo) May 25, 2017
二重振り子は、物理的には、解析力学のラグランジュ方程式によって定式化されます。
振り子の振れ幅が小さいときは、微小振動近似によって固有振動を求めることができますが、振れ幅が大きいときはそうはいきません。
参考:解析力学講義 – 井上順一郎、二重振り子におけるカオス的振舞、二重振り子の精度保証付き数値計算 – kashiの日記
連続力学系
ローレンツ・アトラクター
カオスの視覚的なイメージといえば、ローレンツ・アトラクターが有名でしょう。

画像引用:Chaos7 Attracteurs étranges : L’effet papillon
気象学者のローレンツ(Lorenz)は、大気の変動モデルを研究するために、次の比較的単純なローレンツ方程式を考えました。
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} = -ax +ay \\ \frac{dy}{dt} = -xz + bx -y \\ \frac{dz}{dt} = xy – cz \end{array} \right.\end{aligned} \]
例えば\(x,y,z\)の3成分を、気温、湿度、風の強さと考え、気象現象を表すとみなすことができます。
特定のパラメータのときに、実に複雑な気象現象が起こることを発見したローレンツは、それを「Deterministic Nonperiodic Flow(決定論的で非周期的な流れ)」という論文で発表しています。
上の画像に示されているように、あらゆる気象現象は、チョウチョの羽のような2つの輪っかへと引き込まれていきます。
アトラクター(attractor)とは、周囲の状態を引き寄せる集合のことです。
例えば、安定な不動点や安定なリミットサイクルは、点や閉曲線を描くものが多く、比較的単純なアトラクターです。
しかしながら、ローレンツ・アトラクターは、単純ではありません。
動画を見ればわかりますが、8の字を描きながらもループしているわけではなく、一方の輪ともう一方の輪を不規則に移動します。このような非周期性(nonperiodicity)は、カオスの特徴のひとつです。
参考:カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に
レスラー方程式
ローレンツ方程式とは別の、同じく3変数の常微分方程式でカオスを引き起こすものとして、レスラー方程式(Rössler equation)が知られています。
参考:レスラー方程式
ダフィング方程式
ダフィング方程式(Duffing equation)と呼ばれる、複雑なバネの運動を表す2階の常微分方程式でも、カオスが起こることが知られています。
離散力学系
ロジスティック写像
ロジスティック写像は、生物の個体数の変化を表す数理モデル、ロジスティック方程式を離散化したものです。
\(x_{n+1}=ax_n(1-x_n)\)
さきほどまでの連続的な時間変化が仮定されていたものと異なり、時間変化は離散的です。(連続力学系に対し、離散力学系という。)
ロジスティック方程式では、パラメーター\(a\)が特定の値を取るときに、カオス的な挙動が見られます。(下図では\(r\))

画像引用:LogisticCobwebChaos.gif,Sam Derbyshire – Wikipedia
パラメータ\(a\)によって変化する解の挙動を理解するために、分岐図(bifurcation diagram)がよく使われます。
横軸にパラメータ\(a\)、縦軸に\(x\)の(長期的に)取りうる値を描きます。
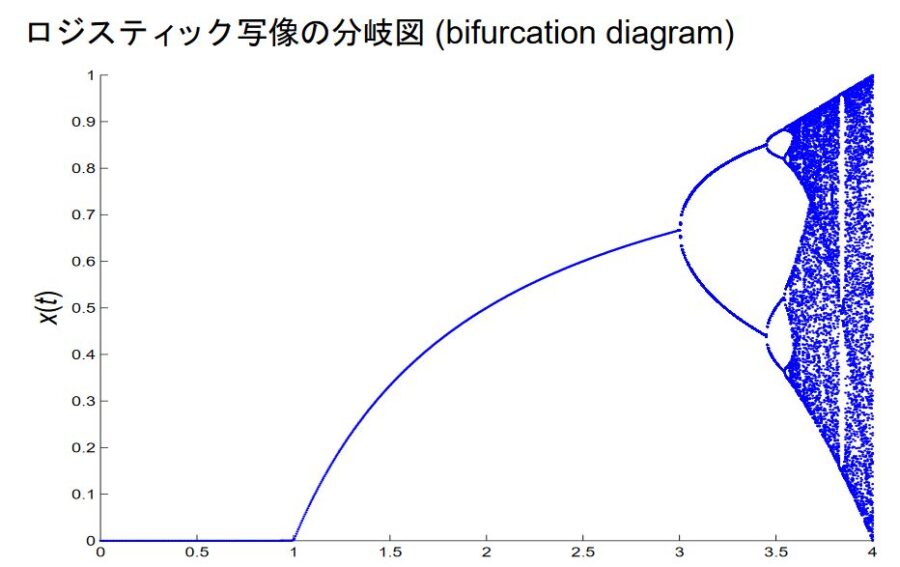
画像引用:カオスと分岐 – 池口研究室
分岐図を見ると、\(0<a<3\)まではシンプルですが、\(3<a<4\)では複雑になり、カオスが起こっています。
\(a=3\)のように、その前後で解の挙動がのパラメータは、分岐点と呼ばれます。\(3<a<4\)では、\(a\)が増すにつれ非常に多くの分岐が起こっているわけです。
この分岐図は、拡大すると同じような分岐図が繰り返されるフラクタル(自己相似)形に近いと言われています。
この分岐図をもとにしたドレスが作られているようです、驚きですね。
参考:二次関数が編み出すドレス-デザイナー松居エリ氏に聞くアートと科学との接点 – マイナビニュース
エノン写像
ロジスティック写像に似た離散力学系としては、エノン写像(Hénon map)が知られています。こちらは2次元(2変数)です。
記号力学系
スメールの馬蹄写像
スメールの馬蹄写像(Smale horseshose map)は、次の画像で表されるような離散力学系です。
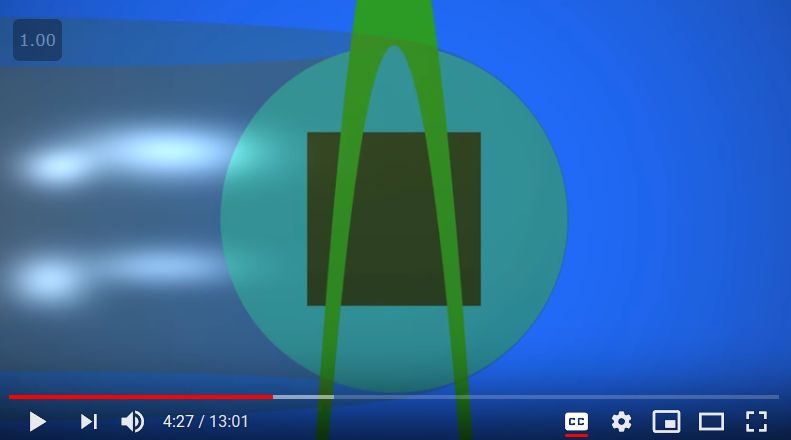
円盤上で定義され、正方形の状態を、タテに引き伸ばし、横に縮め、一定の方向に折り曲げる変換です。
1度の変換で馬の蹄のような形になるので、作者の名前と合わせスメールの馬蹄と呼ばれます。
この写像を繰り返すと、カオスが生じています。
馬蹄の左側をA、右側をBとすると、さまざまな周期解が存在することが示せます。Aだけを通る、Bだけを通るもの(周期1)。AA,AB,BA,BBといったもの(周期2)。
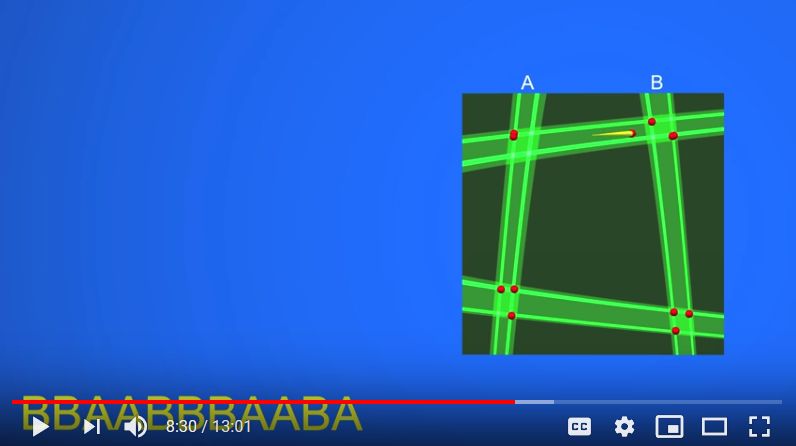
……このようにして、任意の大きさの周期を持った解の存在が示されます。
また、周期解はこの中で到るところにあります。どのような初期状態に対しても、そのほんの少しでもずれた場所に周期解があり、その周期解は多種多様なものであるため、まさしくカオスと言える状況です。
今回のように、ABや01といった記号を使って離散力学系を分析する手法は、記号力学系(symbolic dynamics)と呼ばれています。
参考:Horseshoe map – Wikipedia, Symbolic dynamics – Wikipedia
「カオス」って何?と聞かれたら、やはり二重振り子の動画を見せるのが一番手っ取り早いです。
今回は、その他様々なカオス現象を紹介してみました。多くの方程式・写像で、カオスが生じているのを感じ取れたでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
丸善出版
売り上げランキング: 223,044
シュプリンガー・フェアラーク東京
売り上げランキング: 1,129,481
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで―
共立出版
売り上げランキング: 170,803
Westview Press
売り上げランキング: 62,768
共立出版
売り上げランキング: 1,001,628