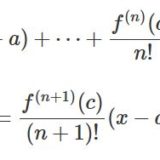どうも、木村(@kimu3_slime)です。
テイラー展開(Taylor expansion)は、大学の微積分学のメイントピックのひとつです。
\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots\end{aligned} \]
しかしながら、教科書に書いてある展開式が複雑で、覚えられない。
何に使うのか、どんな意味があるのか、なぜ学ぶのだろうか? 学部一年生のときの僕は、そんな疑問を抱いた記憶があります。
今回は、単振り子の運動、三角関数(サイン)を例に、テイラー展開の活用例を紹介したいと思います。
テイラー展開=多項式関数による近似
テイラー展開は、いきなり一般形を覚えようとすると苦労します。
まずは三角関数、特にサインのテイラー展開を見てみましょう。
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots \end{aligned} \]
この式の意味を考えてみます。
左辺の\(\sin x\)は、一般にその値を求めるのが簡単ではありません。そんな関数が、右辺ではより簡単な関数、多項式関数によって表されています。図示してみるとわかりやすいです。
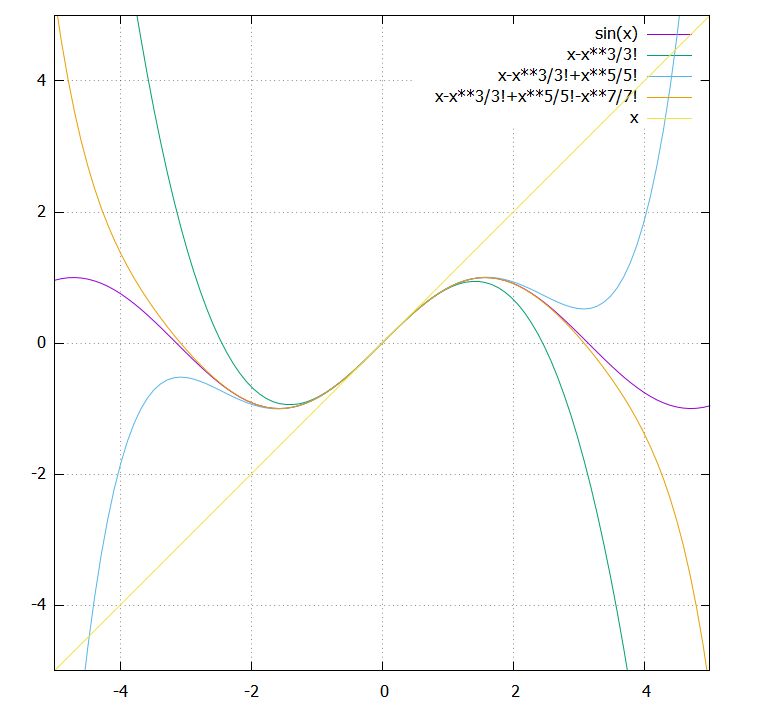
紫色が、\(\sin x\)の曲線です。それに、\(x\)、\(x- \frac{x^3}{3!}\)、\(x- \frac{x^3}{3!}+ \frac{x^5}{5!}\)のグラフを重ねています。
右辺の多項式の項が増えれば増えるほど、\(\sin x\)の曲線により近づいているのがわかるでしょうか? つまり、多項式関数で三角関数(サイン)を近似しているのです。
特に、\(x\)が十分小さい(0に近い)時、グラフの近似具合はとても良いです。そのとき、\(x^3,x^5\)以降の項は\(x\)に比べると十分小さいので、\(\sin x=x\)と近似することができます。
この近似を実際に使ってみましょう。
単振り子の運動方程式を解いてみる
単振り子の運動を考えてみましょう。
天井から長さ\(\ell\)のひもで重さ\(m\)おもりを吊るし、角度\(\theta_0\)から静かに離したとします。
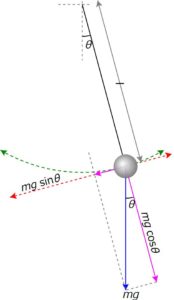
画像引用:File:Pendulum gravity.svg,Krishnavedala
このとき、運動方程式は
\[ \begin{aligned}m \frac{d^2\theta }{d t^2} = -\frac{mg}{\ell}\sin \theta \end{aligned} \]
となります。
右辺が\(\sin \theta\)となっていて、微分方程式は解きにくいです。そこで、振れ幅が小さいときは、さきほどの近似式\(\sin \theta = \theta\)が使えます!
(高校物理では、この近似式によって振り子の運動が説明されます。それがテイラー展開由来のものだったというわけですね。)
\[ \begin{aligned} \frac{d^2\theta }{d t^2} = -\frac{g}{\ell} \theta \end{aligned} \]
右辺が1次関数となったこの形は、とても解きやすいです。
\[ \begin{aligned}\theta(t)=\theta_0 \cos (\sqrt{\frac{g}{\ell}} t) \end{aligned} \]
こちらで解説しました:サイン、コサインは何の役に立つ? バネの振動と三角関数
振れ幅が小さいときの単振り子の運動は、バネの運動と同じになります。つまり、一定の振れ幅で行ったり来たりを続けます(単振動)。
解を見れば、その周期は\(T=2\pi\sqrt{\frac{\ell}{g}} \)とわかります。
つまり、周期は最初に離す位置によらず、一定になる。これが振り子の等時性と呼ばれる性質で、振り子時計の原理となるものです。
ちなみに、近似式が有効と言えるのは、\(\theta\)がどれくらい小さいときでしょうか?
\(\theta- \frac{\theta^3}{3!}+ \cdots\)という式で、3次の項が1次の項の10分の1以下ならば、桁(オーダー)が違うので誤差は少ないと言えるでしょう。
その条件は、\(\frac{ \frac{\theta^3}{3!}}{\theta}<\frac{1}{10}\)を計算すればいいわけです。結果、\(\theta\)が0.77ラジアン=約44°以下なら、誤差は小さいと言えます。
まとめ
テイラー展開の威力、使い方を感じられたでしょうか?
物体の運動に限らず、多く物理現象は微分方程式で書かれます。しかし、いくら方程式が記述できても、出てくる関数が三角関数のように複雑だと、解を明示的に求めるのが難しいです。
そこで役に立つのが、テイラー展開。
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots \end{aligned} \]
と近似・展開できれば、計算が進みやすいです。今回は三角関数\(\sin x\)を例に話しましたが、指数関数や対数関数、累乗根(ルート)関数、二項展開や多項展開、より一般に微分できる関数についても多項式で展開することができます。
いきなり一般形を覚えようとせずに、簡単なケースで近似だと思って使っていけば、自然と展開式も覚えられると思います。
木村すらいむ(@kimu3_slime)でした。ではでは。