どうも、木村(@kimu3_slime)です。
「「集合と位相」をなぜ学ぶのか」を読みました。集合論、位相空間論への入門書としてとても良い本だったのでレビューします。
どんな人向け?
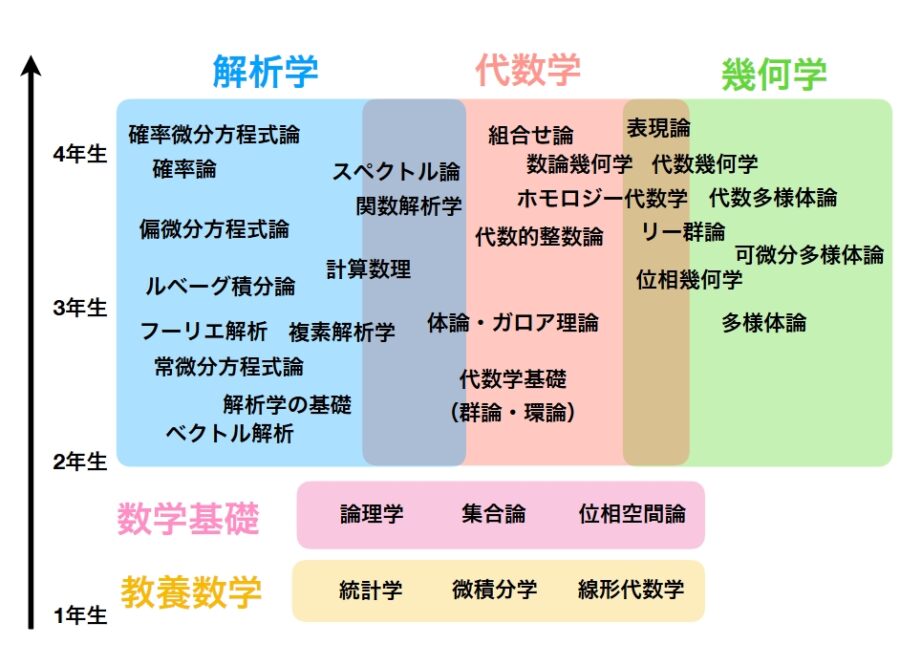
「大学数学のロードマップ ~ 分野一覧と学ぶ順序」で紹介したように、集合論、位相空間論は大学数学の基礎であり、必須の分野です。
数学を記述する基本的な言語と言っても良いでしょう。
その内容は、例えば松坂「集合・位相入門」などの教科書で学ぶことができます。
しかし、なぜ「集合・位相」が基礎科目となっているかは、教科書だけからは理解できません。
なぜこんな抽象的な理論を学ばなければならないか、それは教科書には書いてありません(その応用は、カリキュラム的には後で学ぶことになってしまいます)。
「「集合と位相」をなぜ学ぶのか」は、集合論・位相空間論の教科書ではありません。前書きにもそのことが強調されています。
代わりに、本来なら集合論・位相空間論の授業に盛り込まれるべき周辺の話題、余談が書かれています。
たとえば、本書の最初はフーリエ(1768-1830)の話で、集合論の父・カントール(1845-1918)の約100年前から始まります。
集合と位相にまつわる数学の歴史書として、どんな人物・概念が新たな数学を生み出していったか、その系譜が非常にわかりやすいです。
本書一冊で、集合・位相空間論が習得できるわけではありません(教科書ではないので)。しかしながら、本書は集合・位相空間論を学ぶためのモチベーション、抽象論に進むための生き生きとして数学の姿を伝えてくれます。
「「集合と位相」をなぜ学ぶのか」は、集合・位相空間論の教科書の副読本として持っておきたいところです。
2018年の新しい本なので、僕は初めて読みましたが、学生時代にこの本があったら絶対読んでます。
内容は?
目次を掲載しておきます。
第1章 フーリエ級数と「任意の関数」
第2章 積分の再定義
第3章 実数直線と点集合
第4章 平面と直線は同じ大きさ?
第5章 やっぱり平面と直線は違う
第6章 ボレルの測度とルベーグの積分
第7章 集合と位相はこうして数学の共通語になった
この本を僕が面白いと思うのは、「集合と位相」の話題だけでなく、現代数学の主要なアイデアを紹介してくれているからです。
数学の教科書は、その分野のみの記述に留まり、応用や歴史をあまり伝えてくれないことが多いんですよね。
本書は、熱方程式とフーリエ級数、リーマン積分、デデキントのイデアル論(環論)、ボレルの測度論、ルベーグ積分論、非ユークリッド幾何学(リーマン幾何学)などの話題を含んでいます。
これらは大学のカリキュラムとしては2-4年に「集合と位相」以外で教えられることが多いものですが、集合論・位相論の誕生のきっかけとなる問題を多く含んでいるため、セットで知っておきたいところです。
「任意の関数は三角関数の和として表せる」というフーリエの主張に始まって、「任意の」「関数」とはどういうことか(不連続関数の研究)から点集合の研究へ、ルベーグの収束定理において級数の収束条件がわかりやすくまとめられる……といった話が、人物をキーにしてまとまっています。
いわゆるコーシーやディリクレによる解析学の厳密化、ブルバキの話は僕も知っていましたが、それをフーリエの理論やカントール(集合論)と結びつける話は本書で初めて知り、数学の歴史をより見通しよく理解できたと思います。
「「集合と位相」をなぜ学ぶのか」は、図示・人物紹介によって難しさを減らしながらも、解説できる概念については例・証明を与えるという厳密さを持ち、具体と抽象のバランスがとても良かったです。
(一般向けの本だとふわっとした話しか理解できないか、逆にオタクな話が多くて何が重要なのかわからない、どちらかのことが多いんですよね(笑))
当サイト「趣味の大学数学」もこのスタイルを参考にしてゆきたいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
技術評論社
売り上げランキング: 66,565
こちらもおすすめ
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響