なぜ教養数学として微積分学と線形代数学を学ぶのかブルバキが現代数学に与えた影響

どうも、木村（@kimu3_slime）です。

「大学数学のロードマップ～分野一覧と学ぶ順序」では、教養数学として微積分学、線形代数学を学ぶことを紹介しました。

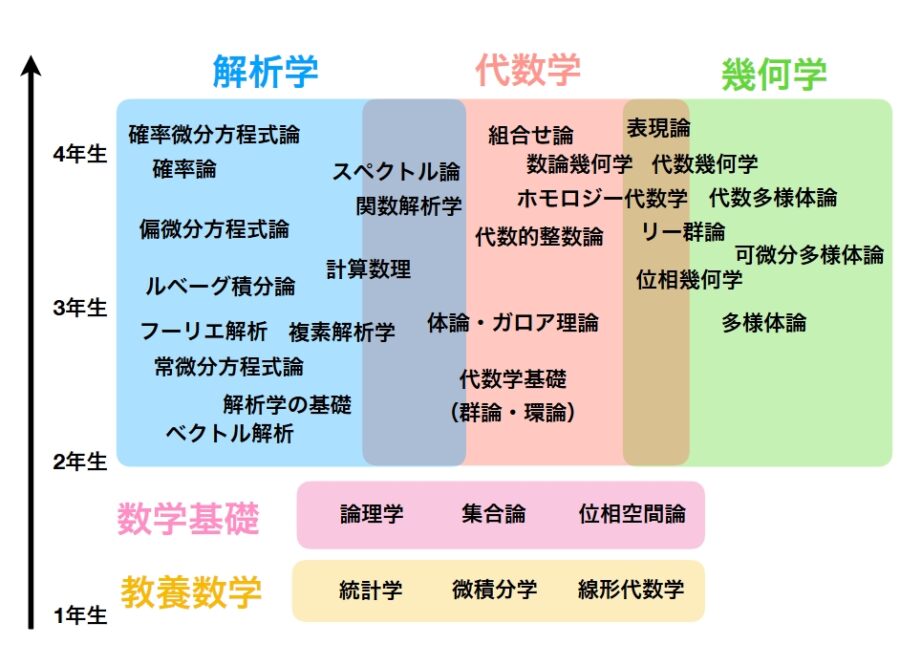
微積分学と線形代数学は、高校の数学の時点でもその入門的な内容が教えられます。

なぜこのようなカリキュラムになっているのでしょうか？　それには、ブルバキと呼ばれる数学者集団が大きく関係しています。

ブルバキとは

ニコラ・ブルバキ（Nicolas Bourbaki）は、フランスの数学者……に見せかけた、数学者集団のペンネームです。

つまり、架空の存在を作り、その名前で教科書を書いていったのです。

ブルバキの正体は長い間不明でしたが、現在では公開されています。エンリ・カルタン、クロード・シュヴァレー、アンドレ・ヴェイユなど、20世紀を代表する有名な数学者たちが、当時30歳前後に所属していたというのだから驚きです。

画像引用：Association des collaborateurs de Nicolas Bourbaki

ブルバキは、「数学原論」という本のシリーズを書きました。

このタイトルは、ユークリッドの（幾何学）「原論」を意識したものでしょう。数学原論は、「原論」のように公理的なアプローチで、厳密さに欠けていた当時の微積分学の教科書を一新しようとしたものでした。

公理についてはこちら：大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう

本のシリーズは何十冊にもわたります。

「集合論」
1.形式的な数学の記述.2.集合論.3.順序集合基数自然数.4.構造.
「代数」
1.代数構造.2.線型代数.3.テンソル代数,外積代数,対称代数.4.多項式と有理式.5.可換体.6.順序群と順序体.7.主環上の加群.8.半単純加群と半単純環.9.準双線型形式と二次形式.
「位相」
1.位相構造.2.一様構造.3.位相群.4.実数.5.一径数群……

微積分学の話をしようとしていたのに、実数の話が登場するのは12冊目、微分の定義は16冊目です（笑）。

僕が大学に入り初めて図書館でブルバキの本を手にとったとき、驚きました。その衝撃は、今でも覚えています。

定義・定理・証明の連続で、直感に訴えるような図もなく、なぜその分野をするのかという説明もなく、ひたすら数学が展開されているのです。

このようなブルバキズム・数学原論のスタイルは、現代数学、また数学教育に大きな影響を与えました。

「ブルバキと「数学原論」 – 斎藤毅」によると、教養数学として微積分学とセットで線形代数学が教えられるようになったのは、ブルバキが線形代数の重要性を強調したからだらだそうです。

「数学原論」の影響は,もっと下の学年にもおよんでいます.今ほとんどの大学の理工系の学部で,1年生は線型代数を学びます.これは,ブルバキが線型代数の重要性を強調したことの帰結です.高校の数学でも,指導要領に復活することになった行列と1次変換について,同じことがいえます.こうしてみると,今,数学を学ぶということの中で,ブルバキ的な数学を身につけることが大きな部分を占めていることがわかります.当時は最新のものだったはずの「数学原論」の目次の各項目が,今はあたりまえのように見えることこそ,その影響の大きさの何よりの証なのです.
別の影響は,数学の記述に見られます.定義,定理,証明の羅列というブルバキの文
体,そして,抽象的,公理的な構成.これらは今の数学の本,教科書,論文で,ふつうに見られるものです.「数学原論」の続きが書かれなくなったのは,他の数学者もブルバキのように書くようになったからということも一因のようです.

引用：ブルバキと「数学原論」 – 斎藤毅

また、このような数学教育のブルバキ化、New Math、現代化と呼ばれる流れは、1960-70年代に各国に広がったそうです。

数理解析講究録「「近代数学」と学校数学 – 数学の普及の歴史から」によると、結局集合論にもとづいた数学の学校教育は、抽象的で難しいために削られてしまい、現代数学のアイディアを普及させるものにならなかったと言います。

確かに、僕が高校生のときの集合論はちょろっとベン図を書くだけで他の分野と結び付けられているようには見えませんでした。また、入学試験でも集合論はあまり問題に出されない分野となっています。

ブルバキのスタイルと現代数学・大学数学は、切っても切れないものです。

僕にとって、集合論を学びそれをベースにあらゆる数学体系が構築できるというアイデアは、大学で数学を学び感動したことのひとつでもあります。

しかしながら、集合論の準備がないまま、（公理的な）微積分学、線形代数学を大学1年でやるのは、やはり手順を飛ばしているのではないかとも、同時に思います。

ブルバキの貢献は大きいですが、ブルバキだけが数学ではありません。ブルバキだって、素朴な解析学を経験した上でそれを抽象化しようとしたわけですから、あらゆる人に具体的な数学経験は必要でしょう。

「趣味の大学数学」では、大学数学で欠けがちな応用・具体例の指摘をしながら、現代数学の紹介をしていきたいと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。