どうも、木村(@kimu3_slime)です。
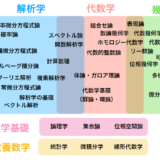
大学数学の基礎として、集合論・位相空間論があります。
あらゆる分野に通ずる基礎的な議論ですが、同時に抽象的で、何のためにやっているのか最初の方はわからなくなりがちです。
僕がこのサイトでまず紹介したい解析学にとって集合位相論は、空間という概念を組み立てるために必要なのです。
今回はそれを図にまとめた上で、ユークリッド空間\(\mathbb{R}^N\)を例に集合、構造、空間とは何かを簡単に紹介します。
ユークリッド空間\(\mathbb{R}^N\)とは
ユークリッド空間とは、ユークリッドが研究した平面幾何学のような空間、またそれを一般化した空間のことです。
\(\mathbb{R}^N\)の\(\mathbb{R}\)は実数(real number)を指しています。実数は、正の整数(自然数\(\mathbb{N}\))、負の整数を含む整数\(\mathbb{Z}\)、分数で表される有理数\(\mathbb{Q}\)だけでなく、\(\sqrt{2},\pi\)のような無理数を含みます。
\(\mathbb{R}^N\)は、文章によってはユークリッド(Euclid)の頭文字を取って、\(E^N\)とも表されます。
\(\mathbb{R}^N\)の\(N\)は空間の次元を指しています。
\(N=1\)のときは、実数、もしくは数直線と呼ばれるものです。単に\(\mathbb{R}\)と書かれることが多いです。\(\mathbb{R}^2\)は平面であり、\(\mathbb{R}^3\)は(3次元)空間です。

4次元以上の一般の次元\(N\)はどう考えれば良いのでしょうか? 例えば平面上の点は\((1,2)\)といったように、2つの実数の組で表されます。この組は視覚的には矢印とも同一視でき、ベクトルとも呼ばれています。三次元なら\((1,0,3)\)と3つの実数の組でひとつの点を表します。\(\mathbb{R}^N\)の点は、\((x_1,x_2,\dots ,x_N)\)と\(N\)個の実数の組と考えれば良いわけです。
ユークリッド空間\(\mathbb{R}^N\)の構造
ユークリッド空間には、構造(structure)が入っています。つまり、単なる実数の集まりではなく、数と数が関係性を持っているのです。
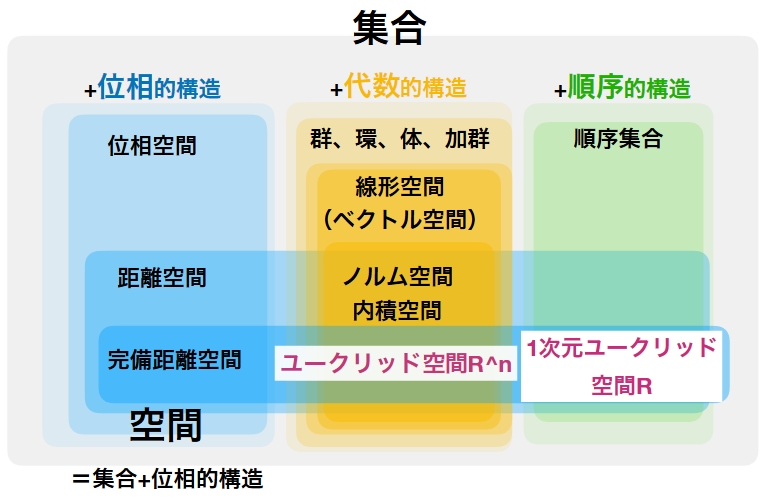
構造には、大まかにわけて3種類あります。位相的構造、代数的構造、順序的構造です。
位相的構造
位相的構造(topological structure)は、点と点のつながり・まとまりを与える仕組みです。
ユークリッド空間では、つながりを与えるものは距離です。2つの点の距離を測ることができるのです。
\(d(\mathbf{x},\mathbf{y})=\sqrt{(x_1 -y_1)^2+\cdots+(x_N -y_N)^2}\)
位相的構造を持った空間を位相空間、距離構造を持った空間を距離空間と言います。ユークリッド空間は、位相空間であり距離空間です。
また、少し難しい話になりますが、ユークリッド空間はある意味で「閉じて」います。実数列(コーシー列)の極限が必ず実数となる、つまり完備性(completeness)を持っています。
完備性を持った距離空間を完備距離空間と言います。ユークリッド空間は、完備な距離空間です。
代数的構造
代数的構造(algebraic structure)とは、足し算や掛け算のような「演算」を与える仕組みです。
基本的な代数的構造としては、群、環、体、加群などがありますが、ユークリッド空間はより多くの構造を持っています。
例えば、ベクトルとベクトルの足し算ができますし、あるベクトルを拡大縮小するスカラー倍という操作もできます。このような性質(他にもいくつか必要ですが)を持った空間を、線形空間(ベクトル空間)と言います。
ユークリッド空間は、線形空間です。
また、単に線形空間であるだけでなく、内積によって2つのベクトルの角度を測ったり、ノルムによって2つのベクトルの距離を測ることができます。
これを、ユークリッド空間は内積空間であり、ノルム空間であると言います。
順序的構造
順序的構造(order structure)とは、\(3<\pi\)のように、2つの要素の順序を比べられる仕組みのことです。
ユークリッド空間\(\mathbb{R}^N\)は、\(N=1\)のときのみ順序構造を持ちます。
数直線には順序をつけられますが、平面以上の空間だと順序はつけられませんよね。
空間=集合+位相的構造
おさらいをしましょう。
ユークリッド空間\(\mathbb{R}^N\)は、位相的構造(距離構造)、代数的構造を持っています。また、\(\mathbb{R}\)は順序的構造を持っています。
つまり、いろいろな条件が整った、かなり性質が良い空間というわけですね。

数学の世界では、数や関数など、研究の対象となるものを集合と呼びます。集合とは、もの(要素)の集まりです。
どんな分野に進んでも、まず何かしらの集合ありきです。そして、集合の要素たちが持っている性質を構造として明確化します。
特に、位相的な構造を持った集合が空間と呼ばれます。
私たちがなんとなくイメージしている空間というものは、単なる数・点の集まりではなく、それらに距離やつながりが想定されているのです。
ユークリッド空間\(\mathbb{R}^N\)は、教養数学においても基本的な対象です。
微積分学では、ユークリッド空間\(\mathbb{R}^N\)上の関数を微分したり積分したりします。線形代数学は、ユークリッド空間\(\mathbb{R}^N\)を例として、代数的な構造、線形空間や線形変換(行列)を考える分野です。
基礎数学である集合論、位相空間論は、ユークリッド空間\(\mathbb{R}^N\)のような対象を一般化するのです。
構造を考えずに、プレーンな立場から集合=もの(要素)の集まりが持つ性質はなんだろうと考えるのが、集合論です。
そして、集合論を土台に位相的構造や距離的構造を考えるのが、位相空間論ですね。
集合論・位相空間論は抽象的ですが、ユークリッド空間\(\mathbb{R}^N\)という具体例を持っていれば臆することはありませんよ。(もちろん他にもいろんな集合や空間を考えますが(笑))
木村すらいむ(@kimu3_slime)でした。ではでは。