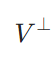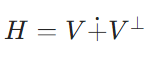どうも、木村(@kimu3_slime)です。
今回は、完備な距離空間の閉集合は完備であることの証明を紹介します。
証明
\((X,d)\)を完備な距離空間、\(A \subset X\)を閉集合とします。このとき、\(A\)が(\(X\)の部分距離空間として)完備であることを証明しましょう。
\((a_n)_n\)を\(A\)におけるコーシー列とします。\(A \subset X\)より、\((a_n)_n\)は\(X\)におけるコーシー列でもあります。\(X\)は完備なのでコーシー列は収束し、\(a_n \to a \quad (n\to \infty)\)を満たす\(a \in X\)が存在します。\(A\)は閉集合なので、その定義のひとつ:\(A\)が極限について閉じていることから、\(a \in A\)です。よって、\(A\)におけるコーシー列が\(A\)において収束するので、\((A,d)\)は完備であることが示せました。
逆の証明
これは逆も成り立ちます。
\(A\subset X\)が完備であるならば、\(A \)は閉集合であることを示しましょう。
そのために、対偶:閉集合でないならば、完備でないことを示します。
閉集合でないことから、\(A\)における収束する点列\((a_n)\)、\(a_n \to a \quad( n\to \infty)\)で、\(a \not \in A\)を満たすものが存在します。収束する点列はコーシー列でもあるので、\((a_n)\)はコーシー列です。よって、コーシー列であって、\(A\)の要素に収束しない点列が存在するので、\(A\)は完備ではありません。
こちらの結果には、\(X\)が完備であることを用いていません。一般的な距離空間において、部分集合は完備ならば閉集合である、というわけです。
完備性を落とした例
全体\((X,d)\)が完備でなければ、\(A \subset X\)が閉集合であっても、それは完備とは限りません。
なぜなら、全体\(A=X\)それ自身は常に閉集合となり(例えば開集合系による位相の定義)、それは完備ではないので。
例えば、ユークリッド距離を考えれば、\(\mathbb{Q}\)において\(\mathbb{Q}\)自身は閉集合ですが、完備ではありません。
以上、完備な距離空間の閉集合は完備であることの証明を紹介してきました。
関数解析においては、バナッハ空間(完備なノルム空間)やヒルベルト空間(完備な内積空間)の閉部分空間をしばしば考えます(例えば直交補空間)。なぜ閉であるかを気にするかといえば、それが完備性を引き継ぐかどうかを決めるから、というわけですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
相対位相、部分集合における開集合・閉集合とは:ユークリッド空間の位相を例に