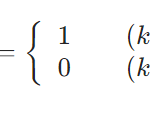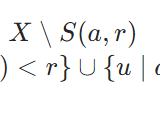距離空間において収束列がコーシー列であることの証明

どうも、木村（@kimu3_slime）です。

今回は、距離空間において収束列がコーシー列であることの証明を紹介します。

距離空間\((X,d)\)における点列\((a_n)\)について考えます。

\((a_n)\)が収束列であるとは、\(\lim_{n\to \infty }a_n =a\)を満たす\(a\)が存在することです。極限の定義は、任意の\(\varepsilon >0\)に対し、「\(n\)が\(n \geq N\)を満たすならば、\(d(a_n,a)< \varepsilon\)」となるような\(N\in \mathbb{N}\)が存在することです。

\((a_n)\)がコーシー列であるとは、任意の\(\varepsilon >0\)に対し、「\(n,m\)が\(n \geq N\)を満たすならば、\(d(a_n,a_m)< \varepsilon\)」となるような\(N\in \mathbb{N}\)が存在することです。

では、点列\((a_n)\)が収束列であるならば、コーシー列であることを証明しましょう。極限を\(\lim_{n\to \infty }a_n =a\)とします。

\(\varepsilon>0\)を任意とします。極限の定義から、「\(n\)が\(n \geq N\)を満たすならば、\(d(a_n,a)< \frac{\varepsilon}{2}\)」となるような\(N\in \mathbb{N}\)が存在します。

\(n,m\)が\(n \geq N\)を満たすとしましょう。このとき、三角不等式と対称性から

\[\begin{aligned} &d(a_n,a_m) \\ &\leq d(a_n,a)+d(a,a_m) \\&= d(a_n,a)+d(a_m,a) \\ & < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} \\&= \varepsilon \end{aligned}\]

となります。よって、コーシー列の定義を満たすことが示せました。同一の\(N\)が利用できるわけですね。

ちなみに、逆「コーシー列であるならば収束列」は、一般に正しいとは限りません。すべてのコーシー列が収束列となるような距離空間は、完備であると呼ばれます。

以上、距離空間において収束列がコーシー列であることの証明を紹介してきました。

対偶「コーシー列でないならば、収束列でない」を用いると、収束しない列が簡単に判定できることがあります。

十分先の2つの項の距離の差が、一定以上に縮まらないことを示せば良いのです。これは\(\ell ^2\)の単位球がコンパクトでないことを示すために応用できます。

木村すらいむ（@kimu3_slime）でした。ではでは。