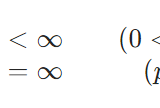どうも、木村(@kimu3_slime)です。
今回は、有界閉区間上の連続関数はp乗可積分であることの証明を紹介します。
p乗可積分とは
連続関数\(f:[a,b]\to \mathbb{R}\)が\(p\)乗可積分であるとは、
- (\(1 \leq p <\infty\)のとき) \(\|f\|_{L^p} := (\int_a^b |f(x)|^p dx )^{\frac{1}{p}} dx <\infty\)
- (\( p =\infty\)のとき) \(\|f\|_{L^\infty} := \inf\{ \lambda \in \mathbb{R} \mid ほとんど至る所で |f(x)|\leq \lambda \}<\infty \)
を満たすことです。p乗して積分した結果が有限であるか、または本質的に有界であるかどうかですね。
\(1 \leq p <\infty\)のとき
\(f\)は有界閉区間\([a,b]\)上で連続なので、最大値と最小値を持ちます。つまり、「すべての\(x \in [a,b]\)に対して\(|f(x) |\leq M\)」を満たす\(M \in \mathbb{R}\)が存在します。
したがって、積分の単調性を用いれば、
\[\begin{aligned} \|f\|_{L^p}& = (\int_a^b |f(x)|^p dx )^{\frac{1}{p}} dx \\ &\leq (\int_a^b M^p dx )^{\frac{1}{p}} \\ &= ((b-a)M^p)^{\frac{1}{p}}\\&<\infty \end{aligned}\]
とp乗可積分であることが示せました。
関数が有界で、かつ積分している範囲も有界なので、何乗して積分した結果も有限の値を持ちます。
「有界閉区間上の連続関数」という条件をつけましたが、「有界な集合上の有界な関数」でも同様に議論できますね。多次元でも成り立ちます。
\(p =\infty\)のとき
さきほど最大値の定理から、\(|f(x) |\leq M<\infty\)なる\(M\)が存在することを確認しました。
したがって特に、\(M\)は「ほとんど至る所で\(|f(x)|\leq \lambda\)」を満たします。よって下限の定義から、
\[\begin{aligned} & \|f\|_{L^\infty} \\ &=\inf\{ \lambda \in \mathbb{R} \mid ほとんど至る所で |f(x)|\leq \lambda \} \\ &\leq M\\&<\infty \end{aligned}\]
となることが示せました。
\( \|f\|_{L^\infty}= \mathrm{ess sup}_x |f(x)|\)は本質的上限、それが有限の値を持つことは本質的に有界とも呼ばれます。一般に、関数が有界ならば本質的に有界というわけです(逆は成り立つとは限らない)。
関数空間の記号を用いたまとめ
連続関数のなす空間は\(C([a,b])\)、\(p\)乗可積分関数のなす空間は\(L^{p}([a,b])\)です。
今回示した結果をこの記号を用いて表せば、\(1 \leq p \leq \infty\)のとき
\[C([a,b]) \subset L^{p}([a,b])\]
ですね。
このような関係は、一般には成り立ちません。例えば非有界な集合\(\mathbb{R}\)において、恒等的に\(f(x)=1\)となる関数は連続ですが、\(\int_{-\infty}^\infty |1|^p dx =\infty\)となり\(p\)乗可積分ではありません。
また、今回の関係を少し一般化した結果として、「\(\mu(\Omega)<\infty\)かつ\(1\leq p <q \leq \infty\)ならば、\(L^q (\Omega) \subset L^p(\Omega)\)」が知られています。
以上、有界閉区間上の連続関数はp乗可積分であることの証明を紹介してきました。
リーマン積分論においては、「有界閉集合の連続関数は(リーマン)可積分である」という結果があります。今回の話は、それを(ルベーグ)p乗可積分に一般化したものと言えます。
今回の話が、p乗可積分関数の具体例や、可積分性の簡単な判定条件として参考になれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)