どうも、木村(@kimu3_slime)です。
今回は、混み具合(人口密度)の計算について、シートの面積と人数の問題を例に紹介します。
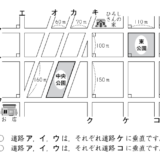
面積が異なる2つのシートに、人が座っています。
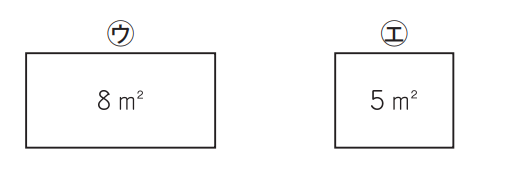
画像引用:平成30年度 全国学力・学習状況調査
| 人数(人) | 面積(㎡) | |
| ウ | 16 | 8 |
| エ | 9 | 5 |
そして上の表のような人数、面積だったとしましょう。
どちらのシートが混んでいるかを調べるために、
\[16 \div 8 =2\]
\[9 \div 5 =1.8\]
という計算をしました。
この計算からわかることを、次の選択肢からひとつ選びましょう。
- 1㎡あたりの人数は2人と1.8人なので、ウのほうが混んでいる
- 1㎡あたりの人数は2人と1.8人なので、エのほうが混んでいる
- 1人あたりの面積は2㎡と1.8㎡なので、ウのほうが混んでいる
- 1人あたりの面積は2㎡と1.8㎡なので、エのほうが混んでいる
これは平成30年度 全国学力・学習状況調査、算数B、□4(2)からの問題です。正答率は50.3%です。
では、解説していきましょう。
これは特定の広さの場所にどれだけの人がいるかを表す数字:人口密度の問題です。算数では、「単位量あたりの大きさ」と呼ばれる単元ですね。
面積\(A\)㎡に\(P\)人の人がいるとき、人口密度\(D\)は
\[D = P \div A = \frac{P}{A}\]
と定義されます。これは1㎡あたりに平均して何人いますか、ということを表す数字です。

例えばウのシートの人口密度を計算すると、\(P=16\)、\(A=8\)なので、
\[ \frac{16}{8} =2\]
となります。人口密度は、2(人/㎡)です。1㎡の面積のシートにつき、2人くらいはいるという混み具合を表しています。
「人/㎡(にん 毎 平方メートル)」は人口密度を表す単位で、1平方メートルに何人いるかを表します。人数を㎡で割ったから、人/㎡です(スラッシュは割り算の意味です)。
(人口密度の単位を単に「人」とするプリント教材もありますが、それは誤解を生みやすいです。「1k㎡あたり~人」と書かないと、基準が曖昧です。)
同様に、エのシートの人口密度を計算すると、
\[9 \div 5 =1.8\]
となり、人口密度は1.8(人/㎡)です。
2(人/㎡)と1.8(人/㎡)を比較すると、同じ面積(1㎡)の人数が多いのは、2(人/㎡)です。したがって、ウのほうが混んでいることがわかりました。問題では、選択肢1が正解です。
ちなみに、人数と面積の割る順序を逆にして、1人あたりの面積がどれだけあるかを考えることによって、混み具合を比較することもできます。
\[B = A \div P = \frac{A}{P}\]
を所有面積と呼ぶことにしましょう(独自の用語です)。単位は、㎡を人で割っているので、㎡/人です。
ウのシートでの所有面積は\(\frac{8}{16}=0.5\)(㎡/人)で、エのシートでの所有面積は\(\frac{5}{9}=0.555\dots\)(㎡/人)です。1人あたりの所有面積が大きいのは、後者ですね。つまり、エのシートの方が空いている(ウが混んでいる)と言えます。
この計算は問題文で提示されたものとは異なるため、選択肢3は正答ではなくなります。しかし、混み具合を比較するための計算としては、これも正解であることに注意しましょう。
社会においては「人/面積」という形の人口密度がよく使われている、というだけの話です。
また、さらなる別解として、面積を揃えてしまうという方法もあります。
| 人数(人) | 面積(㎡) | |
| ウ | 16 | 8 |
| エ | 9 | 5 |
という表において、ウの面積を5倍にしましょう。同じ混み具合を保てば、人数も5倍、\(16\times 5=80\)です。
エの面積を8倍にすると、人数も8倍、\(9\times 8=72\)です。
| 人数(人) | 面積(㎡) | |
| ウ | 80 | 40 |
| エ | 72 | 40 |
40㎡という同じ面積に、80人いるシートと、72人いるシート、どちらが混んでいるでしょうか。前者、すなわちウのシートが混んでいますね。この「面積を揃えて比較する」という発想は、人口密度そのものです。
実際、40㎡あたりの人数を40で割ったものが、さきほど定義した人口密度(人/㎡)となります。
小学校の算数では、単位量あたりの大きさを比較するときに、「人/㎡」といった単位を明示しないことが多いようです。しかし、何と何の比率なのかを意識するために単位は必ず明示したほうが良いと思います。
例えば、50mを10秒で走る人がいたとしましょう。その速さは、
\[\frac{50}{10}=5\]
で、5(m/秒)となります。秒を英語secondで表し、5(m/s)とも。これは秒を基準にした速さ、秒速です。
車の速さは、60(km/時、km/h)のようにしばしば時速で表されます。
こうした割合・比によって定義される数字の意味を知るためには、何を基準としているか(メートルなのか、キロメートルなのか、1秒あたりなのか、1時間あたりなのか)が重要です。
理科、特に物理や化学で、速さや密度など、何かの比率を表す数値を扱うことは多いです。そのときに「この数字は何と何の比率なのか?」を考え、単位を意識すると、割る数と割られる数をひっくり返すような間違えをしにくくなるでしょう。
以上、混み具合(人口密度)の計算について、シートの面積と人数の問題を例に紹介してきました。
割合の計算や意味の読み取りを苦手とする人は多いようですが、「何を何で割った数」なのかを考える癖をつければ、迷うことはなくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)