どうも、木村(@kimu3_slime)です。
今回は、平行四辺形の面積の応用として、どちらが広いか説明する問題を紹介します。
平成19年度全国学力・学習状況調査「小学校 調査問題 算数 B」□5 (3)からの問題です。
次の図において、中央公園と東公園、どちらの面積の方が広いでしょうか。理由をつけて答えましょう。
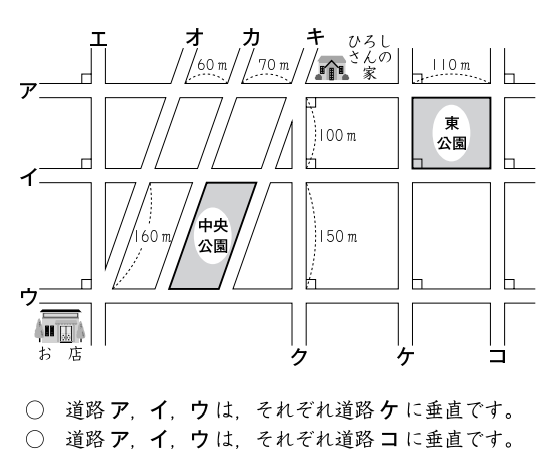

画像引用:平成19年度全国学力・学習状況調査「小学校 調査問題 算数 B」
この問題の正答率は18.2%で、低めとなっています。
では、解説していきます。
「理由をつけて答えましょう」という文で求められていることは、
- 東公園の面積を求める
- 中央公園の面積を求める
- その結果、どちらの面積が大きいか答える
ことです。それぞれの公園の面積を計算してきましょう。
まずは簡単そうな東公園から。
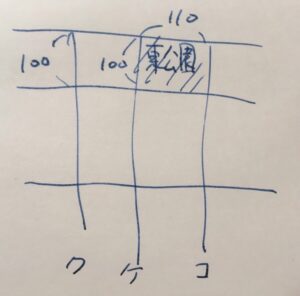
道路ア、イが道路ケ、コに垂直なので、東公園は長方形です。
長方形の面積は、たて×よこ(一辺と隣り合う辺の積)でした。
よこの長さが110であることは、隣に書いてあるのでわかりやすいですが、たての長さはどうでしょうか。
道路クに書いてある長さ100が、道路ケにも対応して、たての長さは100となります。道路ア、イは平行で、平行な直線同士の距離(垂直な線分)の長さは一定、という性質があるからですね。
よって、東公園の面積は\(100 \times 110=11000\)㎡です。
中央公園はどうでしょうか。
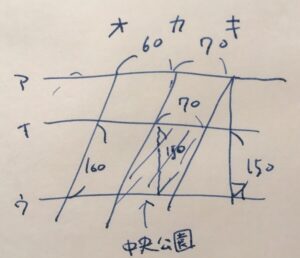
中央公園のふちとなる辺は、直交していないので、長方形ではありません。しかし、道路イ、ウが平行で、道路カ、キも平行なので、中央公園は平行四辺形の形をしています。
平行四辺形の面積は、底辺×高さです。高さとは、底辺とそれに平行な辺との距離、垂直な線分の長さです。
再び平行線同士の距離が一定であることを利用すると、中央公園の底辺として、70mの辺があることがわかります。
これに対する高さはどう求めれば良いでしょうか。もう一つのフチの長さとして、160mを使うのは不適切です。160mの辺は、70mの辺と垂直な関係ではありません。斜めになっていますね。したがって、それは70mの辺を基準とした高さではないのです。
70mの辺に垂直、つまり道路ア、イ、ウに垂直なのは、道路ク、ケ、コですね。したがって、道路クに示された150mの線分が平行四辺形の高さとして使えます。
よって、中央公園の面積は\(70\times 150 =10500\)㎡です。
結果をまとめると、
- 東公園の面積は\(100 \times 110=11000\)㎡
- 中央公園の面積は\(70\times 150 =10500\)㎡
なので、東公園の面積の方が広いことがわかりました。
面積の数字が少し大きくて困った場合は、「10」を基準にくくりだすと簡単になるかもしれません。
\[100\times 110 = (10\times10) \times (11\times 10)\\ = 10\times 11 \times 100\]
\[70\times 150 = (7\times10) \times (15\times 10)\\ = 7\times 15 \times 100\]
となるので、残るのは\(10\times11\)と\(7 \times 15\)の計算ですね。その結果に100をかければ答えが求められます。
以上、どちらが広いか説明する問題、平行四辺形の面積の応用を紹介してきました。
「平行な直線の間隔は一定」という性質に気をつければ、面積の公式においてどの長さを求めれば良いか見抜くことができるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)