余弦定理の証明：ピタゴラスの定理によって

どうも、木村（@kimu3_slime）です。

今回は、ピタゴラスの定理による余弦定理の証明を紹介します。

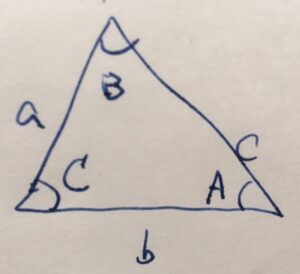
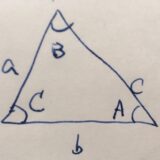
どんな三角形であっても、辺の長さを\(a,b,c\)、角度を\(A,B,C\)とすると

\[a^2+b^2 -2ab \cos C =c^2\]

\[b^2+c^2 -2bc \cos A =a^2\]

\[c^2+a^2 -2ca \cos B =b^2\]

が成り立ちます。これは（第二）余弦定理（law of cosines）と呼ばれるものです。

特に直角な角度について考えると、\(C=90^{\circ}\)ならば\(\cos C=0\)なので、\(a^2+b^2=c^2\)が導かれます。つまり、余弦定理はピタゴラスの定理の一般化で、直角でない三角形にも使えるようになっています。

では、証明していきましょう。

ピタゴラスの定理を使って、長さの関係をコサインを使って表します。

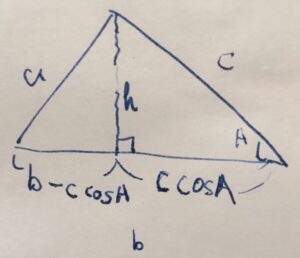
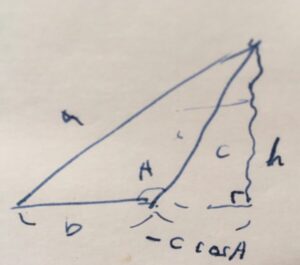
長さ\(b\)を持つ辺へと、向かい合う頂点から垂線を下ろしましょう。高さを\(h\)とします。2つの直角三角形ができました。

右側にできた直角三角形と角度\(A\)に注目すると、コサインの定義から、\(\cos A = \frac{右下側の辺の長さ}{c}\)です。したがって、右下側の辺の長さは\(c \cos A\)となります。

下側の辺の長さは\(b\)なので、分けた三角形における左下側の辺の長さは\(b- c\cos A\)と表せます。

これら2つの三角形の辺の長さに、ピタゴラスの定理を適用すれば、

\[(c \cos A)^2 +h^2 = c^2\]

\[(b-c \cos A)^2 +h^2 = a^2\]

です。\(h^2\)を消すように代入して整理すると、

\[(b-c \cos A)^2 +c^2-(c\cos A)^2 = a^2\]

\[b^2-2bc \cos A +(c\cos A)^2 +c^2-(c\cos A)^2 = a^2\]

\[b^2+c^2 -2bc \cos A = a^2\]

となり余弦定理が証明できました。

この議論の図では\(A\)が鋭角（直角より小さい）となっていますが、鈍角（直角）より大きいケースでも同様です。

長さ\(b\)の辺を延長し、さきほどと同様に垂線を下ろします。

右下にできる直角三角形では、角度\(180^{\circ}-A\)ができます。したがって、右下の辺の長さは\(c \cos (180^{\circ}-A)\)です。鈍角におけるコサインの定義（単位円による定義）から、\( \cos (180^{\circ}-A) =-\cos A\)なので、辺の長さは\(-c \cos A\)となりました。

したがって、2つの直角三角形にピタゴラスの定理を用いれば

\[(-c \cos A)^2 +h^2 = c^2\]

\[(b-c \cos A)^2 +h^2 = a^2\]

となって、さきほどと全く同じ方程式が得られます。

以上の議論では、\(b,c,A\)に注目しましたが、他の記号でも同様にして示せます。

以上、ピタゴラスの定理による余弦定理の証明を紹介してきました。

ピタゴラスの定理の逆と同じように、余弦定理を用いれば長さから角度の情報を求めることができます。

\[ \cos C =\frac{c^2-a^2-b^2}{-2ab}\]

これはベクトルの内積と角度の関係にも応用されるものです。

余弦定理の応用は幅広いですが、基本的にはピタゴラスの定理から導ける、と知ってもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。