どうも、木村(@kimu3_slime)です。
今回は、三角形の面積はなぜ1/2をかけるか、その証明を紹介します。
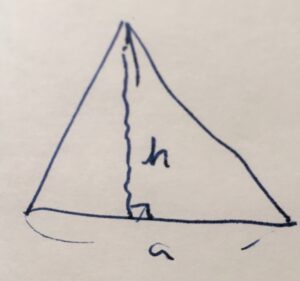
三角形のある辺の長さを\(a\)、それを基準とした高さを\(h\)とするとき、その三角形の面積は\(S=\frac{1}{2}ah\)(底辺かける高さ割る2)となります。
なぜ1/2、半分となるのかは、証明を知ると理解できるでしょう。平行四辺形の半分となるからです。
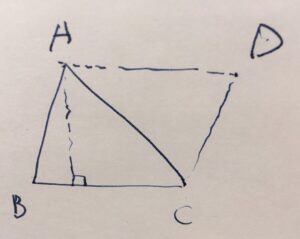
三角形を\(ABC\)としましょう。\(AB,BC\)に平行な直線を引き、その交わる点を\(D\)とします。四角形\(ABCD\)は、向かい合う2組の辺が平行なので、平行四辺形です。
\(AC\)は平行四辺形の対角線なので、\(\triangle ABC,\triangle CDA\)は合同となります。
面積の基本的な性質(公準)として、
- 合同な三角形の面積は等しく
- 重ならない部分に分けて計算求める
ことができます。したがって、
\[\begin{aligned} &(ABCDの面積) \\ &=(ABCの面積) +(CDAの面積) \\&= 2\times (ABCの面積) \end{aligned}\]
です。平行四辺形の面積は、ある辺とそれを基準とした高さの積なので、
\[\begin{aligned} & (ABCの面積)\\ &=\frac{1}{2}\times(ABCDの面積)\\&= \frac{1}{2}ah\end{aligned}\]
となることが示せました。
以上、三角形の面積はなぜ1/2をかけるか、その証明を紹介してきました。
平行四辺形の半分に帰着させて計算できるから、1/2というわけです。ちなみに、平行四辺形の面積は長方形の面積に帰着するので、長方形的な面積の基準を使って三角形の面積が求められているわけですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)