どうも、木村(@kimu3_slime)です。
今回は、台形の中点連結定理とは何か、その証明を紹介します。
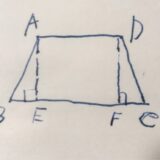
\(AD,BC\)が平行であるような台形\(ABCD\)について、脚\(AB,CD\)の中点を\(M,N\)とします。

このとき、中点をむすぶ線分\(MN\)は底\(AD,BC\)に平行で、長さはそれらの平均\(MN= \frac{1}{2}(AD+BC)\)となります。
これが台形の中点連結定理(midpoint theorem)です。
では、証明していきましょう。補助線を引き、三角形の中点連結定理に持ち込みます。
\(AN,BC\)を直線として延長して(定規による作図)、それらの交点を\(E\)とします。
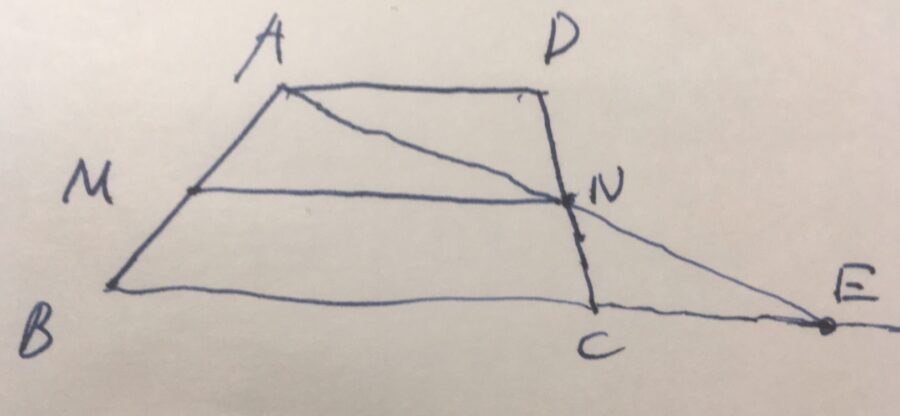
\(AN=NE\)であることを、三角形\(\triangle AND,\triangle ENC\)に注目して示しましょう。
まず、\(N\)は\(CD\)の中点なので、\(ND=NC\)です。一般に対頂角は等しいので、\(\angle AND=ENC\)です。\(AD, EC\)は平行であり、錯角は等しいので、\(\angle ADN=ECN\)です。
したがって、三角形の合同条件、一つの辺の長さとその両端の角度が等しいので(ASA)、\(\triangle AND,\triangle ENC\)は合同です。特に、\(AN=NE\)となることが示せました。
よって、\(\triangle ABE\)において、\(N\)は\(AE\)の中点です。三角形の中点連結定理より、\(MN,BE\)は平行で、\(MN= \frac{1}{2}BE\)となります。
\(BC\)は\(BE\)の一部分なので、\(MN,BC\)は平行です。\(AD,BC\)は平行なので、\(MN,AD\)も平行です。
また、線分の長さを分割すると、\(BE =BC+CE\)です。そして\(\triangle AND,\triangle ENC\)が合同であることから、\(CE=AD\)となっています。
よって、
\[\begin{aligned} &MN \\ &= \frac{1}{2}BE\\&=\frac{1}{2}(BC+CE)\\ &=\frac{1}{2} (AD+BC) \end{aligned}\]
となることが示せました。
以上、台形の中点連結定理の証明を紹介してきました。
台形の場合でも、三角形と似たような中点連結定理が成り立つのは面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)