等脚台形の定義、底角が等しいことの証明

どうも、木村（@kimu3_slime）です。

今回は、等脚台形の定義、底角が等しいの証明を紹介します。

まず、台形（trapezoid）とは、2つの平行な辺を持つ四角形のことです。狭義の台形はちょうど2つの平行な辺を持つもの、広義の台形は2つ以上の平行な辺を持つものですね。

狭義の台形の平行でない2つの辺は、脚（leg）と呼ばれます。そして、脚の長さが等しい台形が、等脚台形（isosceles trapezoid）です。二等辺台形とも。

下の図においては、\(AD,BC\)が平行な辺です。\(AB,DC\)が平行でない辺であり、脚です。今回は\(AB=DC\)であるように、等脚台形であるように描きました。

2つの平行な辺は底辺（上底、下底 base）、脚と底辺のなす角は底角（base angle）と呼ばれます。

さて、等脚台形の性質として、その底角の大きさが等しくなります。

\(AD ,BC\)が平行で、\(AB =CD\)となる等脚台形\(ABCD\)を考えましょう。このとき、底角の大きさが等しくなること\( \angle ABC = \angle DCB\)、\( \angle BAD = \angle CDA\)を証明します。

\(AD =BC\)のときは、正方形となるので、底角は直角で等しいです（狭義の台形なら、このケースは考えなくて良い）。

\(AD \neq BC\)のときを考えます。\(AD < BC\)と仮定して話を進めましょう。\(AD > BC\)のときも同様です。

\(A,D\)を通る\(BC\)の垂線を引き、交わる点を\(E,F\)としましょう。

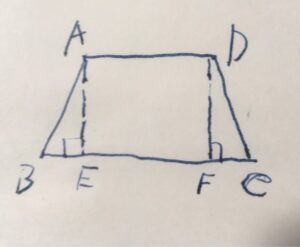
\(\triangle ABE, \triangle DCF\)に注目します。

まず、等脚である仮定から、\(AB=DC\)です。\(AD,BC\)は台形の平行な辺であり、平行な辺同士の距離、垂線の長さは一定なので、\(AE= DF\)です。また、垂線であるので、\(\angle AEB = \angle DFC\)です。

よって、対応する角度は等しいので、\( \angle ABC = \angle DCB\)です。

また同様に、

\[\begin{aligned} &\angle BAD \\ &=\angle BAE+\angle EAD\\&= \angle CDF+\angle FDA \\&= \angle CDA \end{aligned}\]

となり、底角それぞれが等しくなることが示せました。

もちろん、すべての台形が等脚台形であるとは限りません。等脚でない台形も存在します。

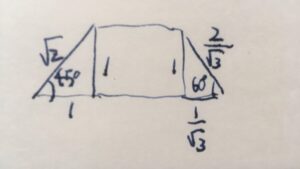
また、今回示したことの逆が成り立つこと：底角が等しい台形は等脚台形となることも知られています。

以上、等脚台形の定義、底角が等しいことの証明を紹介してきました。

等脚であるならば、全体を合同な2つの三角形と長方形に分けられるので、底角も等しくなるわけですね。

典型的な台形の図を描くときは、対称な台形、脚の長さが等しく底角も等しい等脚台形を描くことが多いですが、脚と底角の関係を知っておくときれいに描けるかもしれませんね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ