どうも、木村(@kimu3_slime)です。
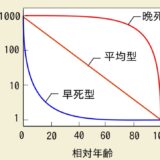
高校生物では、成長曲線と密度効果について学び、次のような曲線を見るでしょう。
画像引用:高等学校生物/生物II/個体群と生物群集 – Wikibooks
これらの曲線は、数学的にどのように得られるのでしょうか。マルサス・ロジスティックモデルについて紹介します。
密度効果がない場合:マルサスモデル
密度効果がないとき、生物の個体数は際限なく倍々ゲームのように増えていきます。
この状況を説明するのが、マルサスモデルと呼ばれる微分方程式です。
生物の個体数を\(u(t)\)と時間の関数で表すとき、
\[\frac{du}{dt} =u\]
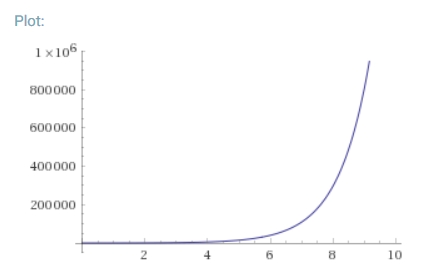
を満たすと考えるのがマルサスモデルです。これは、生物の増殖率は、個体数が増えれば大きくなるという考え方ですね。この方程式の解は、指数関数
\[u(t) = u_0 e^{t}\]
となります。これは指数関数的成長とも呼ばれます。
密度効果がある場合:ロジスティックモデル
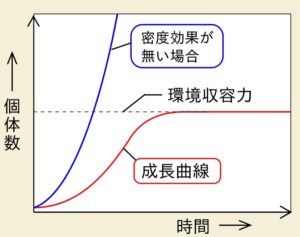
マルサスモデルでは、際限なく個体数が増加します。
実際の生物の個体数増加では、急激に増加する時期はありますが、餌や生存場所などの限界があります。こうした環境による限界を組み込んだモデルが、ロジスティックモデルです。
\[ \begin{aligned}\frac{du}{dt}= ru(1 – \frac{u}{K})\end{aligned} \]
\(r, K>0\)がパラメータです。
\(r\)は、個体数が少ないときの指数的な増殖の速さを表すもので、内的自然増加率(intrinsic rate of natural increase)と呼ばれます。
一方、\(K\)は環境収容力(carrying capacity)と呼ばれ、値が大きいほど最終的に住める個体数が増えます。
マルサスモデルと比較すると、増加率\(u\)だったものが、\(u – u^2\)の形になっています。\(u\)が小さいときは\(u\)の効果によって増殖するのですが、\(-u^2\)によって大きくなりすぎないように歯止めがかかるわけです。
ロジスティック方程式の解は、
\[ \begin{aligned}u(t)= \frac{K}{1+ C e^{-rt}}\end{aligned} \]
\[ \begin{aligned}C = \frac{K}{u(0) } -1\end{aligned} \]
となります。
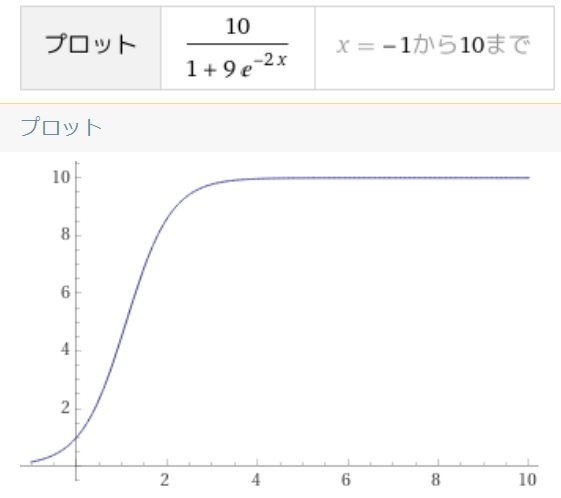
画像引用:WolframAlpha
このS字型の曲線は、ロジスティック曲線やシグモイド曲線と呼ばれます。
内的成長率\(r\)によらず、時間が経過すると、個体数は環境収容力\(K\)に収束します。
\[ \lim_{t \to \infty} u(t)= K \]
実際、ミジンコなどの微生物や小さな昆虫では、ロジスティック曲線に従った増え方をすることが知られています。
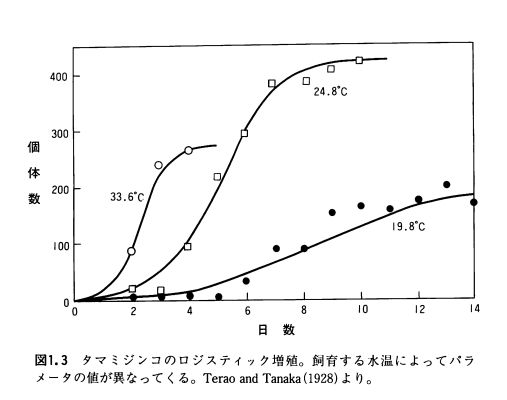
画像引用:巌佐 数理生物学入門―生物社会のダイナミックスを探る
以上、成長曲線と密度効果について、マルサス・ロジスティックモデルによる説明をしてきました。
成長曲線の理論的な背景として、指数関数や微分方程式があることを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
改訂版 日本一詳しい 大学入試完全網羅 生物基礎・生物のすべて
KADOKAWA (2019-03-20T00:00:00.000Z)
¥2,574
数研出版 (2017-02-09T00:00:01Z)
¥2,486 (コレクター商品)
共立出版 (1998-03-01T00:00:01Z)
¥8,800 (コレクター商品)