幾何学・相似の応用：レンズの公式の証明

どうも、木村（@kimu3_slime）です。

今回は、中学で学ぶ幾何学、相似の応用として、レンズの公式の証明を紹介します。

メガネや虫眼鏡、顕微鏡のようなレンズを通して物体を見ると、物体が大きく見えたり小さく見えたりします。人間の目も、仕組みとしてはレンズです。

レンズには光が集まる点、焦点があります。レンズと焦点との距離を焦点距離と呼び、\(f\)としましょう。

物体が発する光がレンズを通ると、像ができあがります。

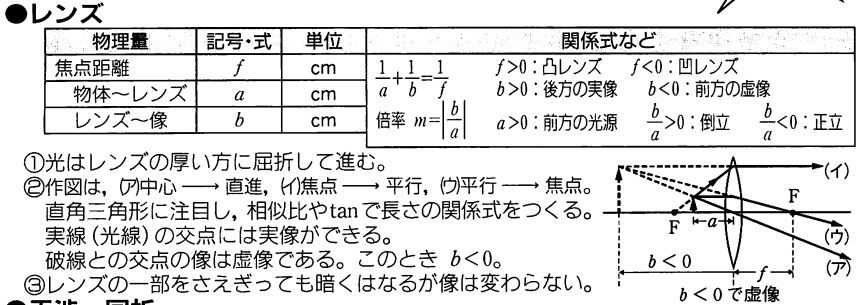
物体とレンズの距離を\(a\)、レンズと像の距離を\(b\)とします。このとき、レンズの公式

\[\frac{1}{a}+\frac{1}{b} = \frac{1}{f}\]

が成り立ちます。ただし、レンズの位置を原点として、\(f,a,b\)の符号は状況に合わせて設定したものです。

今回は簡単のため、凸レンズ（\(f>0\)）で、物体の位置は焦点とレンズの間にあるケースのみ扱います。このときは、虚像ができあがります（\(b<0\)）。

上の図のように三角形の頂点に記号を割り当てて、相似の問題に持ち込んでレンズの公式を証明しましょう。

\(\triangle{AOA^{\prime}}\)と\(\triangle{BOB^{\prime}}\)に注目します。\(\angle AOA^{\prime}\)と\(\angle BOB^{\prime}\)は共通の角であり、\(\angle OAA^{\prime}\)と\(\angle OBB^{\prime}\)はともに直角です。2組の角が等しいので、2つの三角形は相似です \(\triangle{AOA^{\prime}}\sim \triangle{BOB^{\prime}}\)。

したがって、物体と像の高さの比は\(AA^{\prime}:BB^{\prime} = OA:OB=a:-b\)となります。

そして、\(\triangle{OF^{\prime} C}\)と\(\triangle{BF^{\prime} B^{\prime}}\)に注目します。\(\angle OF^{\prime} C\)と\(\angle BF^{\prime} B^{\prime}\)は共通の角であり、\(\angle F^{\prime} OC\)と\(\angle F^{\prime} BB^{\prime}\)はともに直角です。2組の角が等しいので、2つの三角形は相似です \(\triangle{OF^{\prime} C}\sim \triangle{BF^{\prime} B^{\prime}}\)。

したがって、高さの比は\(OC:BB^{\prime} = OF^{\prime}:BF^{\prime}=f:f-b\)です。

ここで、物体から真っすぐ進んだ光がレンズを通して焦点を通るので、\(AA^{\prime}=OC\)となっています。以上によって、

\[AA^{\prime}:BB^{\prime} =a:-b\]

\[OC:BB^{\prime} =f:f-b\]

をまとめれば、

\[a:-b=f:f-b\]

です。比の定義から、

\[a(f-b)= -b f\]

で、\(abf \neq 0\)で割ると

\[\frac{f-b}{bf} = – \frac{1}{a}\]

となり、整理すれば

\[\frac{1}{a}+\frac{1}{b} = \frac{1}{f}\]