どうも、木村(@kimu3_slime)です。
高校物理における近似式とその導出について紹介します。物理重要問題集に載っている、次の近似式を題材にしましょう。
- 三角関数 \(\theta\)が0に近いとき
- \(\sin \theta \simeq \theta\)
- \(\tan \theta \simeq \theta\)
- \(\cos \theta \simeq 1\)
- べき乗 \(\alpha\)を実数として、\(x,y\)が0に近いとき
- \((1+x)^\alpha \simeq 1+\alpha x\)
- \((a+x)^\alpha \simeq a^\alpha (1+ \alpha \frac{x}{a})\)
- \((1+x)(1+y) \simeq 1+x+y\)
近似式の導出
大学の微積分で学ぶ関数の近似、テイラー展開を用いて導出します。
証明について:テイラー展開の展開式の覚え方、導き方、証明、テイラーの定理の積分を用いた導出:積分形の剰余項
三角関数
三角関数のテイラー展開は、次の通りです。
\[ \begin{aligned}\sin x = x – \frac{x^{3}}{3!} +O\left(x^{4}\right)\end{aligned} \]
\[ \begin{aligned}\tan x= x + \frac{x^{3}}{3} +O\left(x^{4}\right)\end{aligned} \]
\[ \begin{aligned}\cos x = 1 – \frac{x^{2}}{2} + O(x^3)\end{aligned} \]
ここで\(O(x^4)\)は\(x^4\)以降の項を表し、\(x\to 0\)でそれ以前の項より速く0に収束します。これはオーダーを表すランダウの記号と呼ばれています。

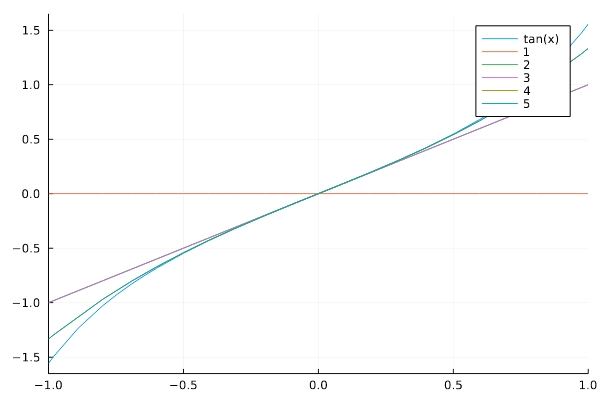
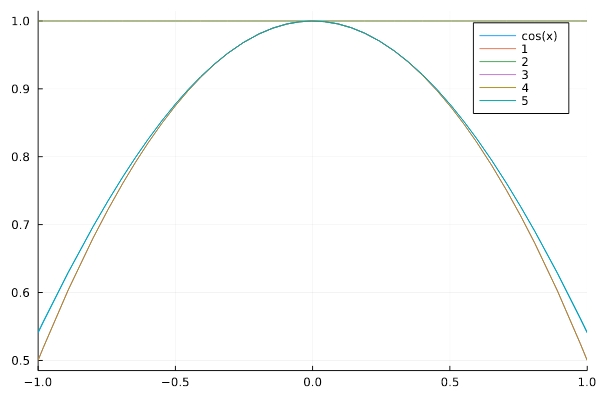
したがって、1次までの項を取り出せば、\(\theta\)が0に近いとき
\[\sin \theta \simeq \theta\]
\[\tan \theta \simeq \theta\]
\[\cos \theta \simeq 1\]
が成り立ちます。この近似は1次までの項を用いているので、1次近似と呼ばれるものです。
3次までの項を用いると、式は複雑になりますが精度があがります。
\[\sin \theta \simeq \theta+\frac{\theta ^3}{6}\]
\[\tan \theta \simeq \theta +\frac{\theta ^3}{3}\]
\[\cos \theta \simeq 1 -\frac{\theta ^2}{2}\]
べき乗
これは二項展開の一般化となる形です。
\[ \begin{aligned}(1+x)^{\alpha} =1 + \alpha x + \frac{\alpha\left(\alpha – 1\right) x^{2} }{2} + O\left(x^{3}\right)\end{aligned} \]
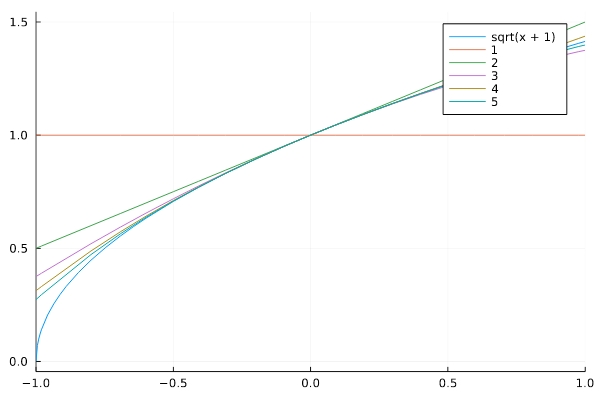
1次までの項を取り出せば、
\[(1+x)^\alpha \simeq 1+\alpha x\]
が得られます。
例えば、\(\alpha =\frac{1}{2}\)ならば
\[\sqrt{1+x} \simeq 1+ \frac{1}{2}x\]
\(\alpha =-1\)ならば
\[\frac{1}{1+x} \simeq 1-x\]
といった近似式が得られます。
\(1+x\)ではなく\(a+x\)のべき乗については、
\[\begin{aligned}(a+x)^\alpha &= a^{\alpha}(1+ \frac{x}{a})^\alpha \\&\simeq a^\alpha (1+ \alpha \frac{x}{a})\end{aligned}\]
となります。
積の形については、
\[\begin{aligned} (1+x)(1+y)&= 1+x+y+xy \\ &=1+x+y+o(\sqrt{x^2+y^2}) \end{aligned}\]
と\(x,y\)の積が1次の項に比べて小さいとみなせるので、
\[(1+x)(1+y) \simeq 1+x+y\]
が成り立ちます。
以上、高校物理における近似式とその導出について紹介してきました。
振り子の運動のように、たとえ問題が簡単な数式で表せたとしても、それが簡単に解けるとは限りません。そこで用いられる近似式は、テイラー展開という方法で導けることを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥990
こちらもおすすめ
有名な極限の公式f(x)/xの覚え方:接線近似とテイラー展開
Julia(SymPy)によるテイラー級数展開の求め方(指数対数、三角、双曲線)