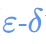どうも、木村(@kimu3_slime)です。
今回は、無相関のt検定について、Juliaによる実践例を交えて紹介します。
相関の検定
2つのサンプルから相関係数を計算することによって、それらに相関があるかどうかを調べることができます。
とはいえ、それはあくまでサンプルの話です。2つの理論的な母集団分布があるとして、それらにも相関があると言って良いのでしょうか? それを調べるのが、2変数の相関の検定(correlation test)です。
\(X,Y\)を2変数の正規分布で、サンプルのサイズを\(n\)としましょう。その相関係数を\(\rho = \mathrm{Cor}(X,Y)\)とします。
帰無仮説を、無相関である\(H_0: \rho =0\)とします。対立仮説は、無相関でない\(H_1 :\rho \neq 0\)です。
帰無仮説が正しいとき、統計量
\[T=\sqrt{n-2} \frac{R}{1-R^2}\]
は自由度\(n-2\)のt分布に従うことが知られています。
サンプルの相関係数を求め、この統計量とt分布を利用すれば、仮説検定が行なえますね。
Juliaによる実践例
では、無相関のt検定について、コンピュータ、Juliaで試してみましょう。
準備として、以下を実行しておきます。
1 | using Statistics, StatsPlots, RDatasets, HypothesisTests |
RDatasets.jlから、アイリス(iris, アヤメ)のデータを使いましょう。
1 | iris = dataset("datasets","iris") |
150 rows × 5 columns
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species | |
|---|---|---|---|---|---|
| Float64 | Float64 | Float64 | Float64 | Cat… | |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
各サンプルに関する、散布図・相関図は次のようになっています。
1 2 | gr(size = (600, 400)) @df iris corrplot(cols(1:4), grid = false, seriescolor = :blue) |
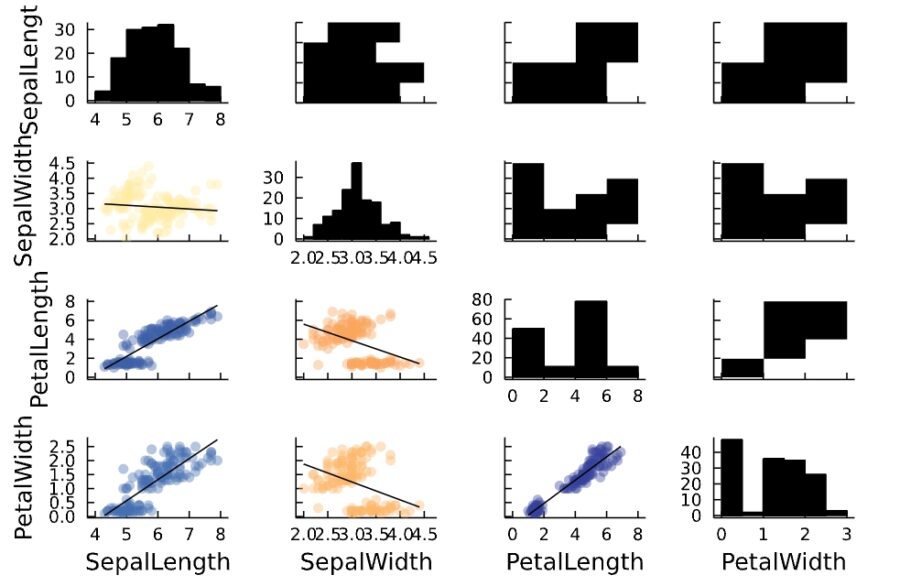
サンプルの相関係数の求め方について詳しくは、「Juliaで散布図・相関図を描き、相関係数を求める方法」にて扱いました。
相関のなさそうな変数、SepalLength(がく片の長さ)とSepalWidth(がく片の幅)について、検定をしてみましょう。ヒストグラムから、正規分布と仮定して話を進めます。
HypothesisTest.jlでは、「CorrelationTest(x,y)」で、帰無仮説を無相関\(\rho =0\)とするt検定ができます。
1 | @df iris CorrelationTest(:SepalLength, :SepalWidth) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | Test for nonzero correlation ---------------------------- Population details: parameter of interest: Correlation value under h_0: 0.0 point estimate: -0.11757 95% confidence interval: (-0.2727, 0.04351) Test summary: outcome with 95% confidence: fail to reject h_0 two-sided p-value: 0.1519 Details: number of observations: 150 number of conditional variables: 0 t-statistic: -1.44029 degrees of freedom: 148 |
5%有意水準では、帰無仮説は棄却されませんでした。つまり、がく片の長さと幅には相関がない可能性があると言えたわけです。
別の相関のありそうな変数、PetalLength(花弁の長さ)とPetalWidth(花弁の幅)について、検定をします。
1 | @df iris CorrelationTest(:PetalLength, :PetalWidth) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | Test for nonzero correlation ---------------------------- Population details: parameter of interest: Correlation value under h_0: 0.0 point estimate: 0.962865 95% confidence interval: (0.9491, 0.973) Test summary: outcome with 95% confidence: reject h_0 two-sided p-value: <1e-85 Details: number of observations: 150 number of conditional variables: 0 t-statistic: 43.3872 degrees of freedom: 148 |
帰無仮説は棄却され、相関があると考えられますね。95%信頼区間を見ても、強い相関があると考えて良いでしょう。
以上、無相関のt検定について、Juliaによる実践例を交えて紹介してきました。
t検定は、平均の検定、平均の差の検定にも使えます。無相関の検定にも使えるので、応用の幅が広いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう
統計的仮説検定とは:平均の検定、t検定を例に、Juliaを使って
2サンプルの平均の差の検定:等サイズ等分散、Juliaを使って