どうも、木村(@kimu3_slime)です。
今回は、適合度のカイ二乗検定とは何か、Juliaによる計算例を紹介します。
適合度のカイ二乗検定とは
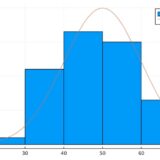
公平かどうかわからないサイコロを、30回振って次のようなヒストグラムが得られたとしましょう。

もし公平なサイコロならば、すべての出目は等確率\(p_1 = \cdots = p_6 = \frac{1}{6}\)です。このサンプルによると、サイコロは公平と言えるでしょうか?
言い換えれば、このサンプルから得られる経験分布は、理論分布(この場合は一様分布)にフィットしていると言えるのでしょうか? それを検証するのが、適合度の検定(goodness of fit test)です。
一般に、\(k\)個の取りうる値がある試行を、\(n\)回行ったとしましょう。
それぞれの値が観測された回数(サンプルの度数)を\(n_1,\dots,n_k\)とします。また、1回の試行でそれぞれの値を取る経験的な確率が\(p_1,\dots,p_k\)であったとします。これは二項分布の一般化、多項分布(multinomial distribution)を考えるということです。
それぞれの値を取る理論的な確率を、\(\theta_1,\dots,\theta_k\)としましょう。調べたい仮説は、経験的に得られた確率が、理論的に推測した確率に適合するかどうか、つまり
\[H_0 : p_i = \theta_i \quad(i =1,\dots,k)\]
です。対立仮説\(H_1\)は、\(H_0\)が成り立たないこととします。
サイコロの例で言えば、\(k=6\)個の値を取る試行を、例えば\(n=30\)回行います。
結果、それぞれの値を取る回数は\((n_1,\dots, n_6)=(3,5,1,9,7,5)\)であり、経験的な確率は\((p_1,\dots, p_6) = (3/30,5/30,1/30,9/30,7/30,5/30)\)です。
調べたい仮説は、サイコロが公平であるかどうかです。つまり理論的な確率を\(\theta_1= \cdots = \theta_6 = \frac{1}{6}\)として、
\[H_0 : p_i = \frac{1}{6} \quad(i =1,\dots,6)\]
という仮説について考えることになります。
多項分布に関する検定は、複雑なものとなります。それを単純化した近似として、次の方法があります。
\(e_i = n \theta_i\)を、それぞれの値の理論的な期待値としましょう。帰無仮説\(H_0\)が正しいとき、統計量
\[\chi^2 = \sum_{i=1}^k \frac{(n_i -e_i)^2}{e_i}\]
は、\(n\)を大きくすると、自由度\(k-1\)のカイ二乗分布に近づくことが知られています。\(\chi^2\)はカイ二乗統計量(chi-squared statistic)と呼ばれるものです。
ホーエル「入門数理統計学」によると、\(k \geq 5, e_i \geq 5\)ならば経験と理論から近似は十分とされています。
カイ二乗検定量を計算し、カイ二乗分布によって確率を求めることで、帰無仮説\(H_0\)が棄却されないか、棄却されるか検定することができます。
この近似による適合度の検定は、ピアソンのカイ二乗検定(Pearson’s chi-square test)と呼ばれるものです。
Juliaによる計算例
ここからは、コンピュータ、Juliaを使って適合度検定、カイ二乗検定を実行してみましょう。
サイコロを30回振った結果のサンプルを作ります。
1 2 3 4 | using Distributions, HypothesisTests, Random, Plots Random.seed!(2022) s = rand(DiscreteUniform(1,6),30) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 30-element Vector{Int64}: 1 6 4 5 4 5 4 6 1 1 4 4 6 ⋮ 3 6 2 6 2 4 5 4 5 5 2 5 |
冒頭で示したヒストグラムは、このサンプルを使って作られました。
1 | histogram(s, bins=6) |

カイ二乗検定をするためには、それぞれの値を取る頻度をまとめたベクトル\(x=(n_1,\dots, n_6)=(3,5,1,9,7,5)\)に変換する必要があります。
これはサンプルから「count」を使うことで可能です。
1 | x = [count(==(i),s) for i in 1:6] |
1 2 3 4 5 6 7 | 6-element Vector{Int64}: 3 5 1 9 7 5 |
Hypothetistests.jlパッケージでは、「ChisqTest(x)」で帰無仮説を等確率とするカイ二乗検定を行えます。
\(x\)は各値の発生頻度を表すベクトルで、各成分は非負の整数でなければなりません。
1 | ChisqTest(x) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.166667, 0.166667, 0.166667, 0.166667, 0.166667, 0.166667] point estimate: [0.1, 0.166667, 0.0333333, 0.3, 0.233333, 0.166667] 95% confidence interval: [(0.0, 0.2747), (0.0, 0.3414), (0.0, 0.2081), (0.1333, 0.4747), (0.06667, 0.4081), (0.0, 0.3414)] Test summary: outcome with 95% confidence: fail to reject h_0 one-sided p-value: 0.1562 Details: Sample size: 30 statistic: 8.0 degrees of freedom: 5 residuals: [-0.894427, 0.0, -1.78885, 1.78885, 0.894427, 0.0] std. residuals: [-0.979796, 0.0, -1.95959, 1.95959, 0.979796, 0.0] |
帰無仮説は棄却されず、このサイコロは公平であるという仮説が正しい可能性があることがわかりました。
\(e_i = n \theta_i = \frac{n}{6}\)なので、サンプルサイズが\(n \geq 30\)でないと、\(e_i \geq 5\)という近似の前提が満たされないことに注意しましょう。小さなサンプルでは公平性を判断するのは難しいです。
(\(e_i\)が5より小さいときは、いくつかの区分を合併して近似の条件が満たされるようにしないと、検定は正しくなくなります。)
違うサンプルとして、等確率でないサイコロからデータを得てみましょう。
\(p\)を確率ベクトル(各値を取る確率を成分とするベクトル)として、試行回数\(n\)の多項分布は「Multinomial(n,p)」で作れます。
偶数の目がでやすいサイコロを作ってみましょう。
1 2 3 | p = [1/12,3/12,1/12,3/12,1/12,3/12] Random.seed!(2022) s = rand(Multinomial(30,p),1) |
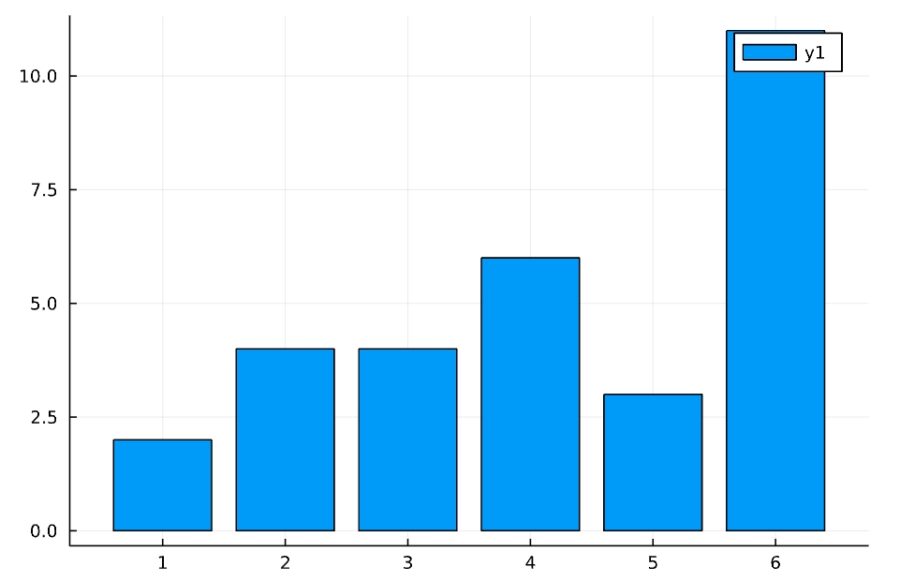
1 2 3 4 5 6 7 | 6×1 Matrix{Int64}: 2 4 4 6 3 11 |
1 | bar(s) |
1 | ChisqTest(s) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.166667, 0.166667, 0.166667, 0.166667, 0.166667, 0.166667] point estimate: [0.0666667, 0.133333, 0.133333, 0.2, 0.1, 0.366667] 95% confidence interval: [(0.0, 0.2398), (0.0, 0.3064), (0.0, 0.3064), (0.03333, 0.3731), (0.0, 0.2731), (0.2, 0.5398)] Test summary: outcome with 95% confidence: fail to reject h_0 one-sided p-value: 0.0647 Details: Sample size: 30 statistic: 10.400000000000002 degrees of freedom: 5 residuals: [-1.34164, -0.447214, -0.447214, 0.447214, -0.894427, 2.68328] std. residuals: [-1.46969, -0.489898, -0.489898, 0.489898, -0.979796, 2.93939] |
検定をすると、5%有意水準では、まだ等確率である仮説は棄却されません。ただし、p値は約0.06であり、10%有意水準なら棄却されますね。
もっとサンプルサイズを大きくしてみましょう。
1 2 3 | p = [1/12,3/12,1/12,3/12,1/12,3/12] Random.seed!(2022) s = rand(Multinomial(50,p),1) |
1 2 3 4 5 6 7 | 6×1 Matrix{Int64}: 3 14 3 16 3 11 |
1 | bar(s) |

このデータを見ると、流石に公平なサイコロとは思い難いですね。実際、それを検証することができます。
1 | ChisqTest(s) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.166667, 0.166667, 0.166667, 0.166667, 0.166667, 0.166667] point estimate: [0.06, 0.28, 0.06, 0.32, 0.06, 0.22] 95% confidence interval: [(0.0, 0.2166), (0.16, 0.4366), (0.0, 0.2166), (0.2, 0.4766), (0.0, 0.2166), (0.1, 0.3766)] Test summary: outcome with 95% confidence: reject h_0 one-sided p-value: 0.0005 Details: Sample size: 50 statistic: 22.000000000000014 degrees of freedom: 5 residuals: [-1.84752, 1.96299, -1.84752, 2.65581, -1.84752, 0.92376] std. residuals: [-2.02386, 2.15035, -2.02386, 2.9093, -2.02386, 1.01193] |
ここまでくるとはっきりと棄却され、このサイコロは公平でないことがわかりました。
\(\theta_0\)として理論的な確率ベクトルを指定することで、等確率ではない帰無仮説についてカイ二乗検定を行うこともできます。
(確率ベクトルを指定するときは、与えるデータを行列でなくベクトルに変換しないとうまく機能しないようです。)
1 2 | theta0 = [1/12,3/12,1/12,3/12,1/12,3/12] ChisqTest(vec(s), theta0) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.0833333, 0.25, 0.0833333, 0.25, 0.0833333, 0.25] point estimate: [0.06, 0.28, 0.06, 0.32, 0.06, 0.22] 95% confidence interval: [(0.0, 0.2166), (0.16, 0.4366), (0.0, 0.2166), (0.2, 0.4766), (0.0, 0.2166), (0.1, 0.3766)] Test summary: outcome with 95% confidence: fail to reject h_0 one-sided p-value: 0.8033 Details: Sample size: 50 statistic: 2.3200000000000025 degrees of freedom: 5 residuals: [-0.571548, 0.424264, -0.571548, 0.989949, -0.571548, -0.424264] std. residuals: [-0.596962, 0.489898, -0.596962, 1.1431, -0.596962, -0.489898] |
理論的な確率が\(\theta_0 =(1/12,3/12,1/12,3/12,1/12,3/12)\)であるという仮説は、棄却されませんでした。
以上、適合度のカイ二乗検定とは何か、Juliaによる計算例を紹介してきました。
今回紹介した考え方を応用して、サンプルから得られる経験的な分布と理論的な分布の適合度を検定することもできます。
この記事を通して、適合度検定の考え方、簡単なケースでのやり方を知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に