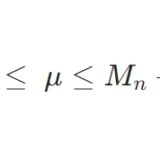どうも、木村(@kimu3_slime)です。
今回は、正規分布の分散の区間推定について、カイ二乗分布を使った方法を紹介します。
分散の区間推定の原理
正規分布から得られたサンプルを使って、その母集団の分散を区間推定する問題を考えましょう。
その区間推定には、カイ二乗分布が使えます。
\(X_1,\dots, X_n\)を一般の正規分布に従う独立な確率変数族(サンプル)とします。\(\sigma ^2\)を母集団の分散、\(S^2\)をサンプルの不偏分散とするとき、統計量
\[Y= (n-1)\frac{S^2}{\sigma ^2}\]
は自由度\(n-1\)のカイ二乗分布に従うことが知られています。
つまり、\(F\)を自由度\(n-1\)のカイ二乗分布の累積分布関数とするとき、\(c_1,c_2\)を実数として
\[P(c_1 \leq Y \leq c_2 ) =F(c_2)-F(c_1)\]
が成り立ちます。
これを変形して、分散\(\sigma ^2\)の信頼区間の形にしましょう。
左辺の中身を変形すると、
\[ c_1 \leq (n-1)\frac{S^2}{\sigma^2}\leq c_2\]
\[ (n-1)\frac{S^2}{c_2} \leq \sigma ^2 \leq (n-1)\frac{S^2}{c_1} \]
となります。
一方、右辺について考えましょう。与えられた信頼水準\(\gamma\)に対し、\(F(c_1) = \frac{1-\gamma}{2}\)、\(F(c_2)= \frac{1+\gamma}{2}\)を満たす\(c_1,c_2\)を求めましょう。つまり、\(c_1 = F^{-1}(\frac{1-\gamma}{2})\)、\(c_2 = F^{-1}(\frac{1+\gamma}{2})\)とします。すると、\(F(c_2)-F(c_1)=\gamma\)ですね。
よって、分散に関する信頼水準\(\gamma\)の信頼区間の定義
\[P( (n-1)\frac{S^2}{c_2} \leq \sigma ^2 \leq (n-1)\frac{S^2}{c_1})=\gamma\]
を導くことができました。
これはサンプル数\(n\)、不偏分散\(S^2\)を使って計算できて、母集団の平均\(\mu\)を使わずに済んでいますね。
分散の信頼区間の求め方
より具体的に、コンピュータ、Juliaを使って分散の信頼区間を計算してみましょう。
正規分布に従う乱数により、20個のサンプルを作りました。
1 2 3 4 5 | using Distributions, Random d1 = Normal(50,10) Random.seed!(2022) x = rand(d1,20) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | 20-element Vector{Float64}: 50.6912301164913 38.84399961848597 42.84480604223728 60.9769650429804 54.978651946367876 33.951339022096505 40.96806064167559 32.42960541746047 49.11909337153176 48.368593011534614 45.130463442688736 66.0313475290611 69.28907743700123 39.33330176391247 42.431065464081925 54.22677747724986 33.47032914639008 54.43764421449241 43.595211148546284 25.114095856632616 |
このサンプルを使って、95%信頼区間を計算します。
\(c_1 = F^{-1}(\frac{1-\gamma}{2})\)、\(c_2 = F^{-1}(\frac{1+\gamma}{2})\)を求めるには、累積分布関数の逆関数「quantile」が使えます。
1 2 3 4 5 6 7 | n = length(x) γ = 0.95 c_1 = quantile(Chisq(n-1), (1-γ)/2) c_2 = quantile(Chisq(n-1), (1+γ)/2) LCL = (n-1)*var(x)/c_2 UCL = (n-1)*var(x)/c_1 println("($LCL, $UCL)") |
1 | (87.47428039117179, 322.6551769389348) |
この区間は、母集団の分散\(\sigma ^2 = 100\)を含むものとなっていますね。サンプル分散が(たまたま)大きめで、上側信頼限界が大きめになりました。
「20個のサンプルから信頼区間を求める」試行を20回行い、分散の信頼区間と、そこに母集団の分散が含まれる割合を表示しましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | k = 20 σ = std(d1) γ = 0.95 c_1 = quantile(Chisq(n-1), (1-γ)/2) c_2 = quantile(Chisq(n-1), (1+γ)/2) in_interval = 0 for i in 1:k x = rand(d1,20) n = length(x) LCL = (n-1)*var(x)/c_2 UCL = (n-1)*var(x)/c_1 println("($LCL, $UCL)") if LCL < σ^2 < UCL in_interval +=1 else end end println(in_interval/k) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | (61.72892773165077, 227.691591293349) (75.88516663601004, 279.9078970240201) (50.22170985655, 185.2463902243931) (37.58748993277255, 138.64416101184796) (26.094102026481178, 96.24997277790257) (45.04360414218315, 166.14657473570048) (85.94704198019724, 317.02184817627074) (62.32212451455588, 229.87964030720715) (65.4881071438079, 241.55759502554054) (52.790526516328924, 194.72165529863202) (96.5836692789844, 356.25581326608295) (37.921877179140836, 139.87757242901662) (75.47928975971644, 278.41079096324074) (29.481035218792613, 108.7429195453262) (79.00929295445748, 291.43146172841716) (32.755691416022856, 120.821724538138) (28.80725313513159, 106.25762585157125) (88.84153562119148, 327.6983962279638) (50.41047439306601, 185.94266179881484) (48.224496745999744, 177.87952596797803) 0.95 |
運の要素はありますが、ちょうど95%の割合で母集団の分散を含んでいますね。1個の例「(26.094102026481178, 96.24997277790257)」のみ含んでいません。
試行回数をk=10000に増やすと、信頼区間が母集団分散を含んでいる割合として0.9482が得られました。これは\(\gamma\)に近い値で、95%信頼区間の意味です。
信頼区間の幅(大きさ)は、
\[\begin{aligned}&\quad ((n-1)\frac{S^2}{c_1} )-( (n-1)\frac{S^2}{c_2} ) \\&=(n-1)S^2(\frac{1}{c_1 }-\frac{1}{c_2})\end{aligned}\]
です。\(\gamma \to 1\)のとき、\(c_1\to 0\)、\(c_2 \to \infty\)なので、信頼水準を上げるほど区間の幅は広がります。
また、サンプル数\(n\)を増やすと、カイ二乗分布が正規分布に近づいていく性質(中心極限定理)より、信頼区間の幅は狭まることが知られています。\(n-1\)の部分は不偏分散でキャンセルされていることに注意。
サンプル数を増やしたときに、信頼区間の幅の長さがどう変化するか、実験してみましょう。
1 2 3 4 5 6 7 8 9 10 11 | k = 10^4 γ = 0.95 for n in 2:10^3:k Random.seed!(2022) x = rand(d1,n) c_1 = quantile(Chisq(n-1), (1-γ)/2) c_2 = quantile(Chisq(n-1), (1+γ)/2) LCL = (n-1)*var(x)/c_2 UCL = (n-1)*var(x)/c_1 println("n=$n ",UCL-LCL) end |
1 2 3 4 5 6 7 8 9 10 | n=2 71445.80308144813 n=1002 18.753963589279493 n=2002 12.558722261825864 n=3002 10.394916651389806 n=4002 9.044440027704226 n=5002 8.057674482958063 n=6002 7.288094252822546 n=7002 6.714429875306905 n=8002 6.25436278802151 n=9002 5.883695088479442 |
確かにサンプル数が多いほど、信頼区間の幅が小さくなっていることがわかりますね。
以上、正規分布の分散の区間推定について、カイ二乗分布を使った方法を紹介してきました。
t分布による平均の区間推定と合わせて、区間推定の基本的な方法として知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
区間推定、信頼区間とは:分散既知の正規分布における平均の推定を例に
点推定、不偏推定量とは:平均と分散を例に、なぜn-1で割るのか