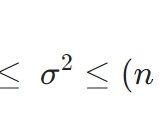正規分布の平均の区間推定：分散未知、t分布を使って

どうも、木村（@kimu3_slime）です。

今回は、正規分布の平均の区間推定について、分散未知、t分布を使った方法を紹介します。

平均の区間推定の原理
信頼区間の求め方
こちらもおすすめ

平均の区間推定の原理

正規分布から得られたサンプルを使って、その母集団の平均を区間推定する問題を考えましょう。

分散$\sigma ^2$が既知であるとき、正規分布を使って区間推定することができました。

ただし、普通は分散を知らないから推定をするわけです。

t分布を用いると、分散が未知であるケースでも、平均の区間推定ができることを紹介しましょう。

$X_1,\dots, X_n$を一般の正規分布に従う独立な確率変数族（サンプル）とします。$M_n$をサンプル平均、$S^2$を不偏分散とするとき、統計量

\[T= \frac{M_n -\mu}{\frac{S}{\sqrt{n}}}\]

は自由度$n-1$のt分布に従うことが知られています。

つまり、$F$を自由度$n-1$のt分布の累積分布関数とするとき、$c>0$を実数として

\[P(-c \leq T \leq c ) =F(c)-F(-c)\]

が成り立ちます。

これを変形して、平均$\mu$の信頼区間の形にしましょう。

左辺の中身を変形すると、

\[ -c \leq \frac{M_n -\mu}{\frac{S}{\sqrt{n}}} \leq c\]

\[ -c\frac{S}{\sqrt{n}} \leq M_n -\mu \leq c\frac{S}{\sqrt{n}}\]

\[ M_n-c\frac{S}{\sqrt{n}} \leq \mu \leq M_n+ c\frac{S}{\sqrt{n}}\]

となります。

一方、右辺はt分布が対称であることから、$F(-c)=1- F(c)$が成り立ちます。与えられた信頼水準$\gamma$に対し、

\[2F(c)-1 = \gamma\]

\[c = F^{-1}(\frac{\gamma +1}{2})\]

を満たす$c$を求めましょう。すると、信頼水準$\gamma$の信頼区間の定義

\[P( M_n-c\frac{S}{\sqrt{n}} \leq \mu \leq M_n+ c\frac{S}{\sqrt{n}})=\gamma\]

を導くことができました。

これはサンプル平均$M_n$、サンプル数$n$、不偏分散$S^2$を使って計算できるので、母集団の分散$\sigma^2$を使わずに済んでいますね。

信頼区間の求め方

より具体的に、コンピュータ、Juliaを使って信頼区間を計算してみましょう。

正規分布に従う乱数により、20個のサンプルを作りました。

using StatsPlots, Random

d1 = Normal(50,10)
Random.seed!(2022)
x = rand(d1,20)

using StatsPlots, Random

d1 = Normal(50,10)

Random.seed!(2022)

x = rand(d1,20)

20-element Vector{Float64}:
 50.6912301164913
 38.84399961848597
 42.84480604223728
 60.9769650429804
 54.978651946367876
 33.951339022096505
 40.96806064167559
 32.42960541746047
 49.11909337153176
 48.368593011534614
 45.130463442688736
 66.0313475290611
 69.28907743700123
 39.33330176391247
 42.431065464081925
 54.22677747724986
 33.47032914639008
 54.43764421449241
 43.595211148546284
 25.114095856632616

20-element Vector{Float64}:

50.6912301164913

38.84399961848597

42.84480604223728

60.9769650429804

54.978651946367876

33.951339022096505

40.96806064167559

32.42960541746047

49.11909337153176

48.368593011534614

45.130463442688736

66.0313475290611

69.28907743700123

39.33330176391247

42.431065464081925

54.22677747724986

33.47032914639008

54.43764421449241

43.595211148546284

25.114095856632616

このサンプルを使って、95%信頼区間を計算します。

$c = F^{-1}(\frac{\gamma +1}{2})$を求めるには、累積分布関数の逆関数「quantile」が使えます。

n = length(x)
γ = 0.95
c = quantile(TDist(n-1), (γ+1)/2)
LCL = mean(x)-c*std(x)/sqrt(n)
UCL = mean(x)+c*std(x)/sqrt(n)
println("($LCL, $UCL)")

n = length(x)

γ = 0.95

c = quantile(TDist(n-1), (γ+1)/2)

LCL = mean(x)-c*std(x)/sqrt(n)

UCL = mean(x)+c*std(x)/sqrt(n)

println("($LCL, $UCL)")

(40.94783184755752, 51.67533392353432)

1	(40.94783184755752, 51.67533392353432)

この区間は、母集団の平均$\mu = 50$を含むものとなっていますね。サンプル平均が（たまたま）50よりやや小さく、下側に寄った信頼区間となりました。

「20個のサンプルから信頼区間を求める」試行を20回行い、信頼区間と、そこに母集団の平均が含まれる割合を表示しましょう。

k = 20
μ = mean(d1)
γ = 0.95
c = quantile(TDist(n-1), (γ+1)/2)
in_interval = 0
for i in 1:k
    x = rand(d1,20)
    n = length(x)
    LCL = mean(x)-c*std(x)/sqrt(n)
    UCL = mean(x)+c*std(x)/sqrt(n)
    println("($LCL, $UCL)")
    if LCL < μ < UCL
        in_interval +=1
    else    
    end
end
println(in_interval/k)

k = 20

μ = mean(d1)

γ = 0.95

c = quantile(TDist(n-1), (γ+1)/2)

in_interval = 0

for i in 1:k

x = rand(d1,20)

n = length(x)

LCL = mean(x)-c*std(x)/sqrt(n)

UCL = mean(x)+c*std(x)/sqrt(n)

println("($LCL, $UCL)")

if LCL < μ < UCL

in_interval +=1

else

end

println(in_interval/k)

(46.97317460919723, 54.988440429621164)
(42.199028653561285, 50.65446309687108)
(45.54742079988635, 54.4851855294048)
(43.062429428234616, 53.48256078118015)
(46.50306190798204, 52.96484757048248)
(44.323552198308974, 53.43018077107236)
(43.54355717803865, 55.35572546960875)
(49.52634217718501, 58.771893613726654)
(47.70717106740368, 54.677711110921095)
(41.67699953002105, 52.47222168206095)
(46.854534087746046, 54.862532068261984)
(43.82875432324889, 55.03954496856986)
(44.756848433444375, 53.22719079279344)
(47.541290976273146, 56.4896858231502)
(38.327206992784475, 50.609255779423556)
(48.17742827092914, 55.72253171406783)
(46.694379793826016, 54.727458685742945)
(44.18733966799515, 51.92025009282183)
(45.77354506461891, 56.1674381970519)
(44.94164604937353, 54.95802704025486)
1.0