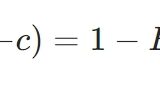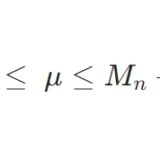カイ二乗分布とその性質、Juliaによる計算方法

どうも、木村（@kimu3_slime）です。

今回は、カイ二乗分布とその性質、Juliaによる計算方法を紹介します。

カイ二乗分布とは
カイ二乗分布の性質
累積分布関数の計算
こちらもおすすめ

カイ二乗分布とは

カイ二乗分布（$\chi^2$分布, chi-squared distribution）は、確率密度関数

\[ f(x) =\begin{cases} \frac{1}{2^{\frac{\nu}{2}} \Gamma(\frac{\nu}{2})}x^{\frac{\nu}{2} – 1} e^{-\frac{x}{2}} & (x>0 )\\0 & (0 \leq x)\end{cases}\]

を持つ確率分布です。ここで$\Gamma$はガンマ関数です。

パラメータ$\nu$（ニュー）は1以上の自然数で、自由度（degrees of freedom）と呼ばれています。

$\nu=2$のとき、$x$のべき乗の部分が消え、シンプルな形になります。$\Gamma(1)=1$なので、

\[f(x)=\frac{1}{2} e^{-\frac{x}{2}} \]

です。これは$\lambda =\frac{1}{2}$の指数分布と呼ばれています。

カイ二乗分布の一般化として、ガンマ分布があります。ガンマ分布において$k= \frac{\nu}{2},\theta =2$のケースがカイ二乗分布です。

いくつかの自由度でのカイ分布のグラフを、コンピュータ、Juliaで描いてみましょう。

「Chisq(ν)」で自由度$\nu$のt分布が表せます。その確率質量関数は、「pdf(Chisq(ν),x)」です。

using Distributions, StatsPlots

function Chisqplot(k)
    p = plot()
    x = 0:0.1:10
    for n in 1:2:k
        f(x) = pdf(Chisq(n),x)
        p = plot!(x,f,label="ν=$n", xlims=[0,10])
    end
    display(p)
end

Chisqplot(10)

using Distributions, StatsPlots

function Chisqplot(k)

p = plot()

x = 0:0.1:10

for n in 1:2:k

f(x) = pdf(Chisq(n),x)

p = plot!(x,f,label="ν=$n", xlims=[0,10])

end

display(p)

end

Chisqplot(10)

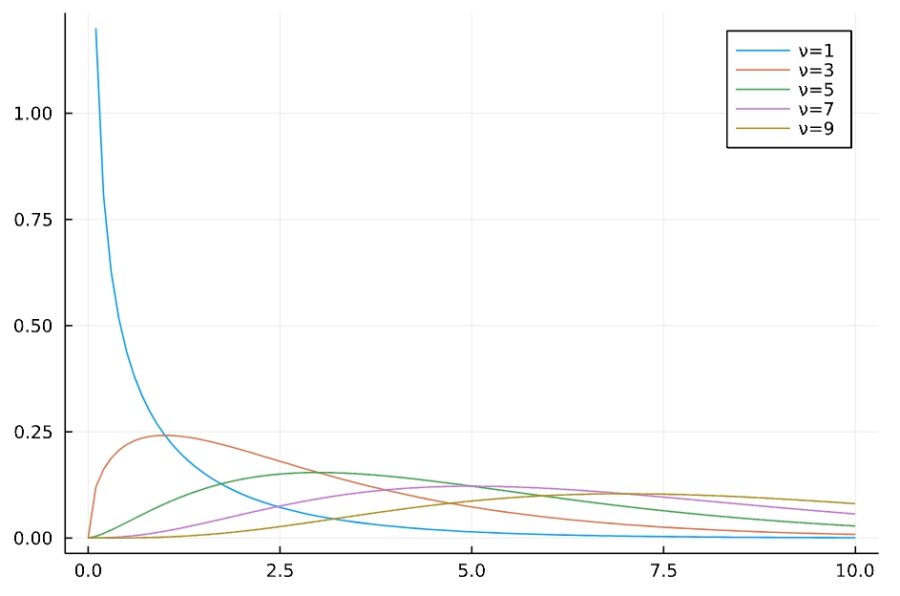
$\nu =1$のとき、$x$の負べきとなるので原点が発散します。$\nu \geq 3$のとき、必ず原点を通り、自由度が大きくなるほど山が右側へ移動していきます。無限遠方では、指数関数の効果によって必ず減衰しますね。

また、正規分布やt分布と違って、平均について対称ではありません。

カイ二乗分布の性質

カイ二乗分布の名前の由来は、標準正規分布に従う独立な確率変数族$X_1,\dots,X_n$の二乗の和

\[X_1 ^2 +X_2^2+\cdots+X_n ^2\]

が、自由度$n$のカイ二乗分布に従うことです。

その応用としては、平均を未知としたときの正規分布の分散の区間推定があります。

一般の正規分布に従う独立な確率変数があるとき、不偏分散$S^2$を

\[S^2 = \frac{1}{n-1}\sum_{k=1}^n (X_k – M_n )^2\]

\[M_n = \frac{1}{n}\sum_{k=1}^n X_k\]

とするとき、統計量

\[Y :=(n-1) \frac{S^2}{\sigma ^2} \]

は自由度$n-1$のカイ二乗分布に従うことが知られています。

この統計量は母集団の平均$\mu$を使わずにサンプルから計算でき、母集団の分散$\sigma^2$を含むので、推定に使えます。

正規分布に従う乱数によって得られたサンプルから二乗和と$Y$を計算し、それがカイ二乗分布に従っているか確かめてみましょう。

「サンプル10個を取り出し、二乗和・$Y$を計算する」ことを10000回行い、それを正規化したヒストグラムとして図示し、自由度$10-1=9$のカイ二乗分布と比較してみました。

d = Normal(0,1)
n = 10
k = 10000
χsq = zeros(k)
for i in 1:k
    x = rand(d,n)
    χsq[i] = sum(x.^2)
end
histogram(χsq, normalize=true)
plot!(Chisq(n))

d = Normal(0,1)

n = 10

k = 10000

χsq = zeros(k)

for i in 1:k

x = rand(d,n)

χsq[i] = sum(x.^2)

end

histogram(χsq, normalize=true)

plot!(Chisq(n))

d = Normal(50,10)
n = 10
k = 10000
Y = zeros(k)
for i in 1:k
    x = rand(d,n)
    Y[i] = (n-1)*var(x)/var(d)
end
histogram(Y, normalize=true)
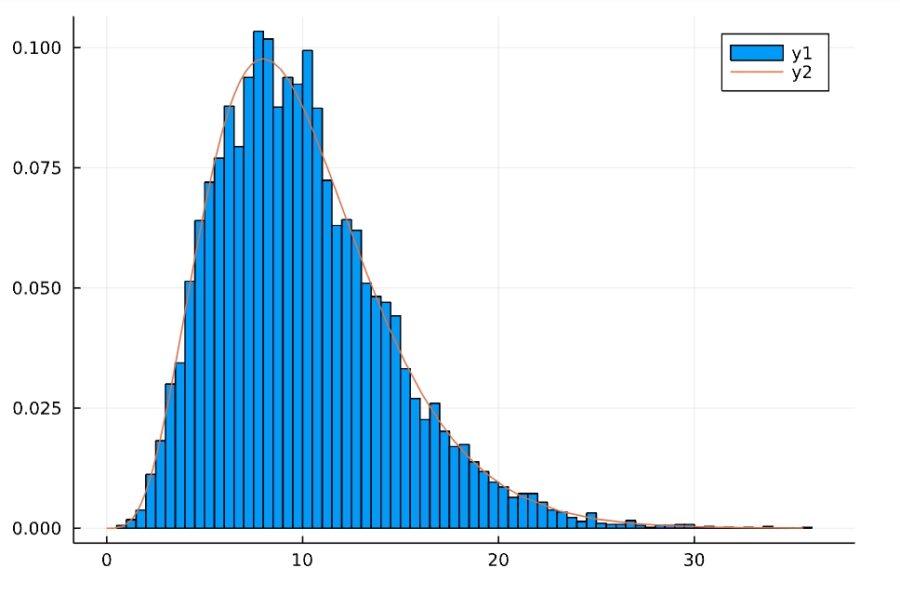
plot!(Chisq(n-1))

d = Normal(50,10)

n = 10

k = 10000

Y = zeros(k)

for i in 1:k

x = rand(d,n)

Y[i] = (n-1)*var(x)/var(d)

end

histogram(Y, normalize=true)

plot!(Chisq(n-1))

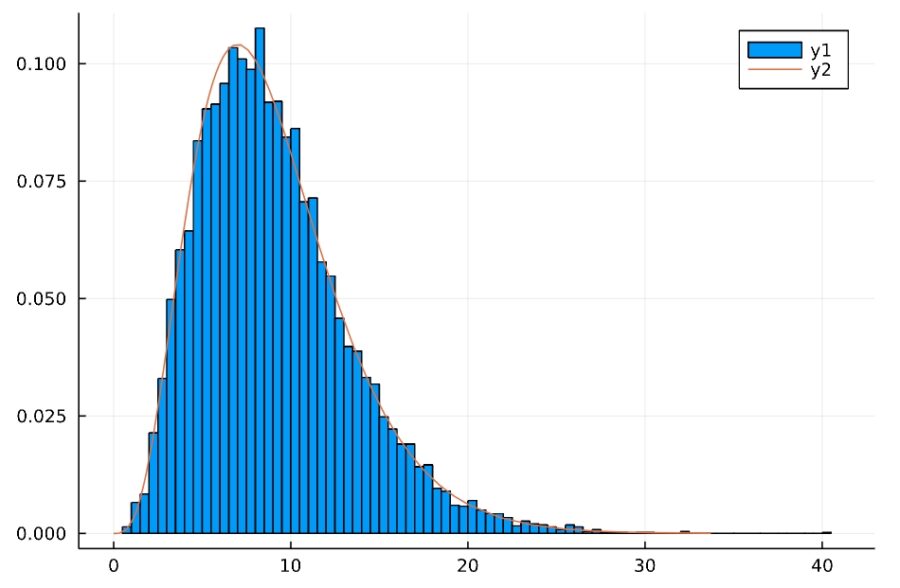
確かにこれらの統計量がカイ二乗分布に従っていそうなことがわかります。

d = Normal(50,10)
n = 3
k = 10000
Y = zeros(k)
for i in 1:k
    x = rand(d,n)
    Y[i] = (n-1)*var(x)/var(d)
end
histogram(Y, normalize=true)
plot!(Chisq(n-1))

d = Normal(50,10)

n = 3

k = 10000

Y = zeros(k)

for i in 1:k

x = rand(d,n)

Y[i] = (n-1)*var(x)/var(d)

end

histogram(Y, normalize=true)

plot!(Chisq(n-1))

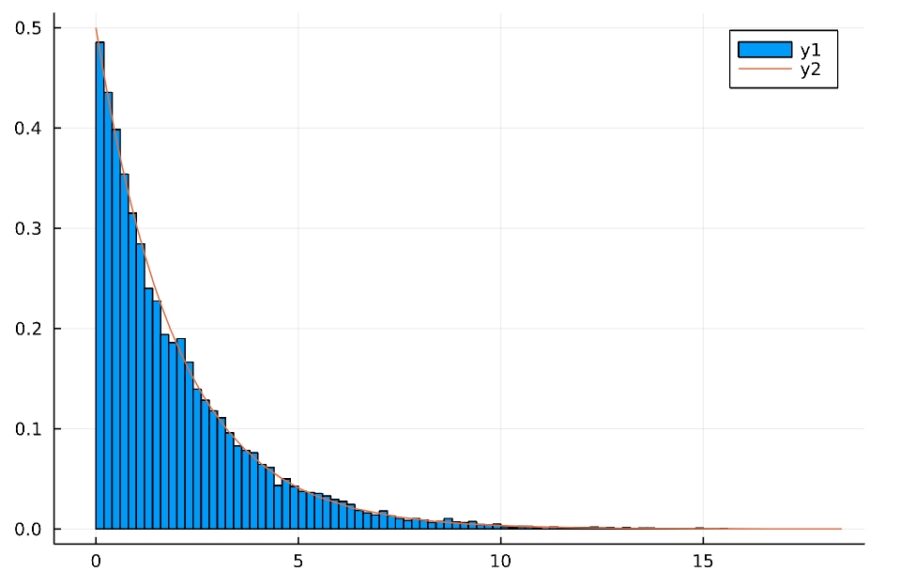
自由度を変えても、確かにカイ二乗分布になっていますね。

累積分布関数の計算

カイ二乗分布を使った区間推定などでは、その累積分布関数$F$に関する計算が必要です。

カイ二乗分布の数値は教科書やウェブ上でまとまっていますが、ここではJuliaで求めてみましょう。

「cdf」で累積分布関数が作れます。

F(x) = cdf(Chisq(9),x)
plot(F, xlims=[0,30])

1 2	F(x) = cdf(Chisq(9),x) plot(F, xlims=[0,30])

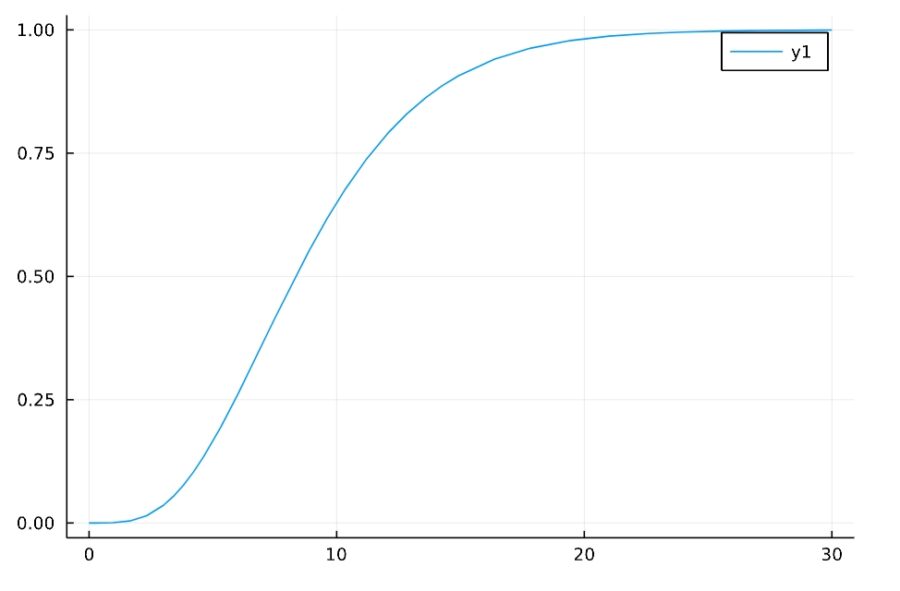
区間推定では、与えられた$\gamma$に対し、$F(c_1)=\frac{1-\gamma}{2}$（左側確率）、$F(c_2)=\frac{1+\gamma}{2}$（右側確率）を満たす$c_1,c_2$を求める必要があります。

「quantile」で累積分布関数の逆関数が求められます。

サンプルサイズが10のとき、いくつかの$\gamma$について$c_1,c_2$を求めてみましょう。

n = 10
Γ = [0.9,0.95,0.99,0.999]
println("ν=$(n-1)")
for γ in Γ
    println("γ=$γ  ")
    println("c_1  ",quantile(Chisq(n-1) , (1-γ)/2))
    println("c_2  ",quantile(Chisq(n-1) , (1+γ)/2) , "\n")
end

n = 10

Γ = [0.9,0.95,0.99,0.999]

println("ν=$(n-1)")

for γ in Γ

println("γ=$γ ")

println("c_1 ",quantile(Chisq(n-1) , (1-γ)/2))

println("c_2 ",quantile(Chisq(n-1) , (1+γ)/2) , "\n")

end

ν=9
γ=0.9  
c_1  3.3251128430668144
c_2  16.918977604620448

γ=0.95  
c_1  2.7003894999803584
c_2  19.02276779864163

γ=0.99  
c_1  1.7349329049966606
c_2  23.589350781257384

γ=0.999  
c_1  0.9716994489578404
c_2  29.665808103596422

ν=9

γ=0.9

c_1 3.3251128430668144

c_2 16.918977604620448

γ=0.95

c_1 2.7003894999803584

c_2 19.02276779864163

γ=0.99

c_1 1.7349329049966606

c_2 23.589350781257384

γ=0.999

c_1 0.9716994489578404

c_2 29.665808103596422

もっと直接的に、$F(c)=p$を満たす$c$を求めてみましょう。

n = 10
P = [0.005,0.01,0.025,0.05, 0.90,0.95,0.975,0.99,0.995]
println("ν=$(n-1)\n")
for p in P
    println("p=$p  ")
    println(quantile(Chisq(n-1) , p),"\n")
end

n = 10

P = [0.005,0.01,0.025,0.05, 0.90,0.95,0.975,0.99,0.995]

println("ν=$(n-1)\n")

for p in P

println("p=$p ")

println(quantile(Chisq(n-1) , p),"\n")

end

ν=9

p=0.005  
1.73493290499666

p=0.01  
2.0879007358707273

p=0.025  
2.700389499980358

p=0.05  
3.3251128430668153

p=0.9  
14.683656573259839

p=0.95  
16.918977604620448

p=0.975  
19.02276779864163

p=0.99  
21.665994333461924

p=0.995  
23.589350781257384