どうも、木村(@kimu3_slime)です。
今回は、対称な確率密度関数を持つ累積分布関数の計算
\[F(-c) = 1-F(c)\]
を紹介します。
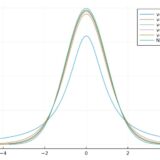
連続確率分布があり、その確率密度関数\(f\)が\(x=0\)を軸として対称\(f(x)=f(-x)\)(偶関数)であったとしましょう。また、累積分布関数を
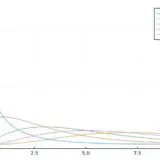
\[F(x)= \int_{-\infty}^x f(s)ds\]
とします。
このとき、実数\(c>0\)について
\[F(-c) = 1-F(c)\]
が成り立ちます。
積分区間を分けて計算すると、
\[\begin{aligned} F(-c)&= \int_{-\infty}^{-c} f(s)ds \\ &= \int_{-\infty}^\infty f(s)ds -\int_{-c}^\infty f(s)ds\\&= 1 – \int_{c} ^{-\infty} (-f(-t) )dt \\&= 1- \int_{-\infty}^c f(-t)dt \\&= 1-\int_{-\infty} ^c f(t)dt \\&= 1- F(c)\end{aligned}\]
となるので。全区間での確率が1になる\(\int_{-\infty}^\infty f(s)ds =1\)のは、確率密度関数(または累積分布関数)の定義によるものです。
ちなみに、\(G(c):=1-F(c)\)は相補累積分布関数(CCDF; complementary cumulative distribution function)と呼ばれます。つまり、\(f\)が偶関数のとき、\(F(-c)\)は相補累積分布関数になると言い換えられるわけです。
この性質は、次のように言い換えることもできます。
\(f(x)=f(-x)\)のとき、\(\int_{-\infty}^0 f(x)dx= \int_{0}^\infty f(x)dx\)なので、\(2F(0)=1\)です。これを使えば、\(F(c)-F(0)=-(F(-c)-F(0))\)が成り立ちます。これは点\((0, F(0))\)に関してグラフが点対称(平行移動すれば奇関数)ということです。
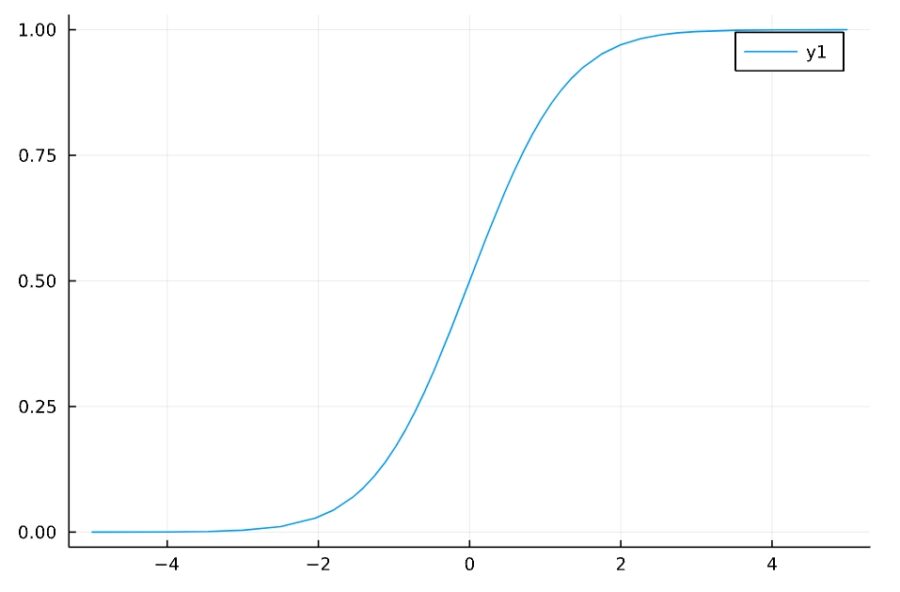
\(F^{-1}(\frac{1}{2})\)は一般に中央値であり、もし\(f\)が偶関数ならば、\(x=0\)が中央値となります。
\(F(-c) = 1-F(c)\)という性質があると、累積分布関数は正の値\(F(c)\)がわかれば、すべて求めることができます。これによって累積分布関数の表が簡略化できます。
区間推定においては、平均0を中心とした95%の確率\(\gamma\)に対応する区間を求める問題が登場します。つまり、\(F(c)-F(-c)= \gamma\)となる\(c\)を求めたいです。
正規分布やt分布は対称な確率密度関数を持ちます。
そこで\(F(-c)=1-F(c)\)を用いれば、\(2F(c)= 1+\gamma\)で、\(c= F^{-1}(\frac{1+\gamma}{2})\)と解くことができます。
以上、対称な確率密度関数を持つ累積分布関数の計算を紹介してきました。
よく使われる計算方法なので、導けるようになると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)