どうも、木村(@kimu3_slime)です。
今回は、Juliaで線形回帰、最小二乗法で回帰直線を描く方法を紹介します。
参考:Juliaで散布図・相関図を描き、相関係数を求める方法
準備
RDatasets, StatsPlots, GLMを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("RDatasets") Pkg.add("StatsPlots") Pkg.add("GLM") |
準備として、以下のコードを実行しておきます。
1 | using Statistics, RDatasets, StatsPlots, GLM |
線形回帰、最小二乗法で回帰直線を描く方法
RDatasets.jlから、アイリス(iris, アヤメ)のデータを使いましょう。
1 | iris = dataset("datasets","iris") |
150 rows × 5 columns
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species | |
|---|---|---|---|---|---|
| Float64 | Float64 | Float64 | Float64 | Cat… | |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
各変数での散布図、相関図は、次のようにして得られます。
1 | @df iris corrplot(cols(1:4), grid = false) |
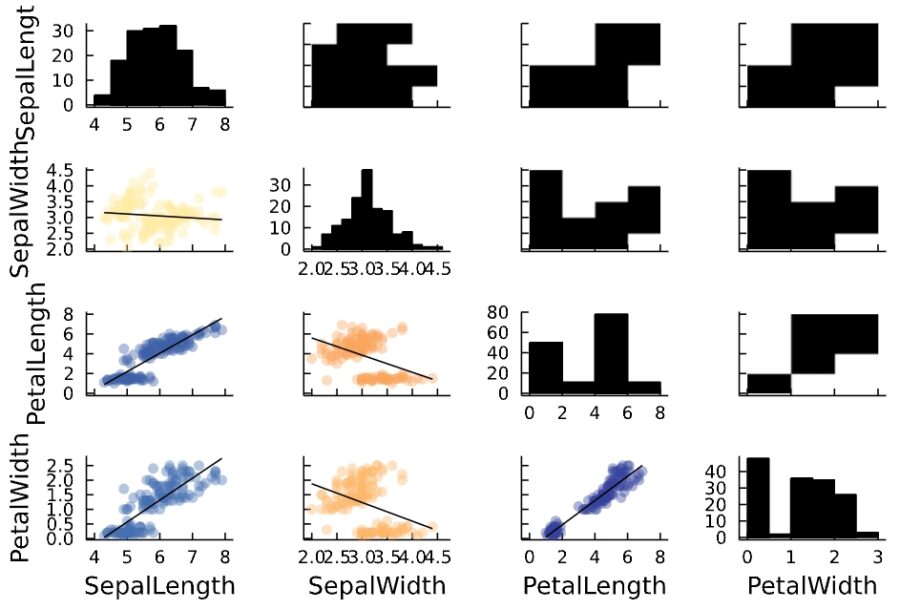
図は得られますが、データを近似する直線(回帰直線)を得る方法がわかりません。
相関係数の一覧、相関係数は次の通り。
1 | @df iris cor(cols(1:4)) |
1 2 3 4 5 | 4×4 Matrix{Float64}: 1.0 -0.11757 0.871754 0.817941 -0.11757 1.0 -0.42844 -0.366126 0.871754 -0.42844 1.0 0.962865 0.817941 -0.366126 0.962865 1.0 |
線形回帰、最小二乗法とは
線形回帰(linear regression)は、データ\((x_1,\dots,x_N),(y_1,\dots,y_N)\)を使って、変数\(x,y\)間の関係を直線\(y= a+bx\)(線形モデル)として予測する考え方です。
切片\(a\)、傾き\(b\)を推測する必要がありますが、その方法として最小二乗法(least squares method)が知られています。それは残差の二乗和(RSS, residual sum of squares)
\[\sum_{i=1}^n \varepsilon_i ^2 = \sum_{i=1}^n (y_i -(a+bx_i))^2\]
を最小化する\(a,b\)を求める方法です。
簡単な例
「ls1 =fit(LinearModel,@formula(Y ~ X), データフレーム)」で、データフレームの2つの変数間について、最小二乗法による線形回帰モデルを作ります。
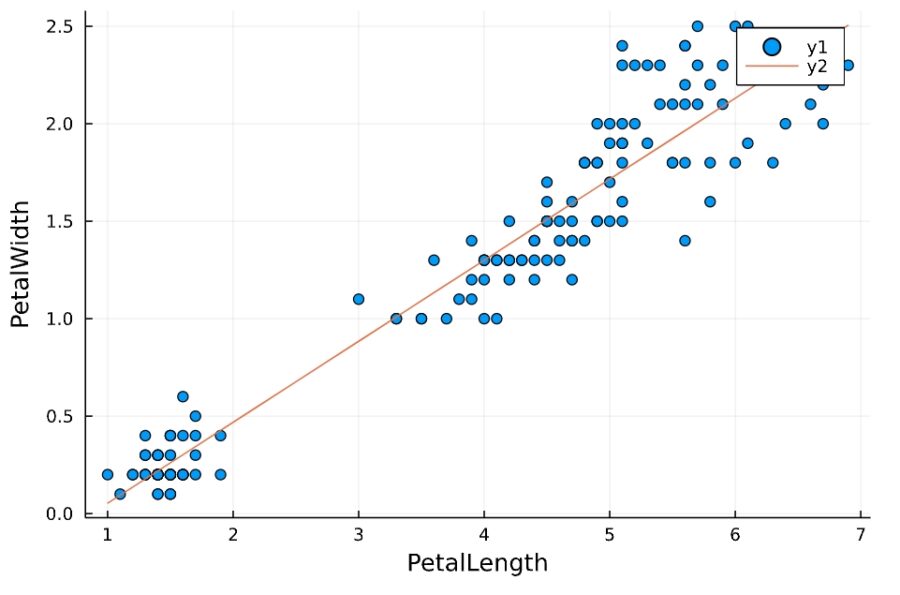
1 | ls1 =fit(LinearModel,@formula(PetalWidth ~ PetalLength), iris) |
1 2 3 4 5 6 7 8 9 10 11 | StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}} PetalWidth ~ 1 + PetalLength Coefficients: ───────────────────────────────────────────────────────────────────────── Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95% ───────────────────────────────────────────────────────────────────────── (Intercept) -0.363076 0.039762 -9.13 <1e-15 -0.44165 -0.284501 PetalLength 0.415755 0.00958244 43.39 <1e-85 0.396819 0.434691 ───────────────────────────────────────────────────────────────────────── |
Coef.が回帰係数、すなわち切片と傾きの推測値です。Std. Errorは、推定量の標準偏差=標準誤差(standard error)で、推定の精度を表します。
他にも、回帰係数が0であるかどうかについてのt検定におけるt値とp値、推定量の95%信頼区間の下限と上限が示されています。
「coef(回帰モデル)」で、回帰係数を取り出せます。
1 | coef(ls1) |
1 2 3 | 2-element Vector{Float64}: -0.3630755213190342 0.4157554163524127 |
これを使えば、散布図と回帰直線を合わせた図が作れますね。
1 2 3 | f(x) = coef(ls1)[1] + coef(ls1)[2]*x @df iris scatter( :PetalLength, :PetalWidth , xlabel="PetalLength", ylabel="PetalWidth") plot!(f) |
一般化
ここまでの結果を一般化して、データフレームと2つの変数名を与えたら、回帰係数を求め、散布図と回帰直線を描く関数を作りましょう。
1 2 3 4 5 6 7 | function linear_regression_plot(df, nameX::String, nameY::String) ls =fit(LinearModel, Term(Symbol(nameY)) ~ Term(Symbol(nameX)), df) display(ls) f(x) = coef(ls)[1] + coef(ls)[2]*x scatter( df[:,Symbol(nameX)], df[:,Symbol(nameY)] , xlabel="$(nameX)", ylabel="$(nameY)") display(plot!(f)) end |
回帰モデルの作成で「@formula(PetalWidth ~ PetalLength)」と書いていた部分を、「Term(Symbol(nameY)) ~ Term(Symbol(nameX))」と一般化しました。
fitの第2変数では特定の書式に則った数式が必要で、StatsModels.jlのConstructing a formula programmaticallyを参考に書いています。
試してみましょう。
1 | linear_regression_plot(iris, "SepalWidth", "PetalWidth") |
1 2 3 4 5 6 7 8 9 10 11 | StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}} PetalWidth ~ 1 + SepalWidth Coefficients: ───────────────────────────────────────────────────────────────────────── Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95% ───────────────────────────────────────────────────────────────────────── (Intercept) 3.15687 0.413082 7.64 <1e-11 2.34057 3.97317 SepalWidth -0.640277 0.133768 -4.79 <1e-05 -0.904619 -0.375934 ───────────────────────────────────────────────────────────────────────── |
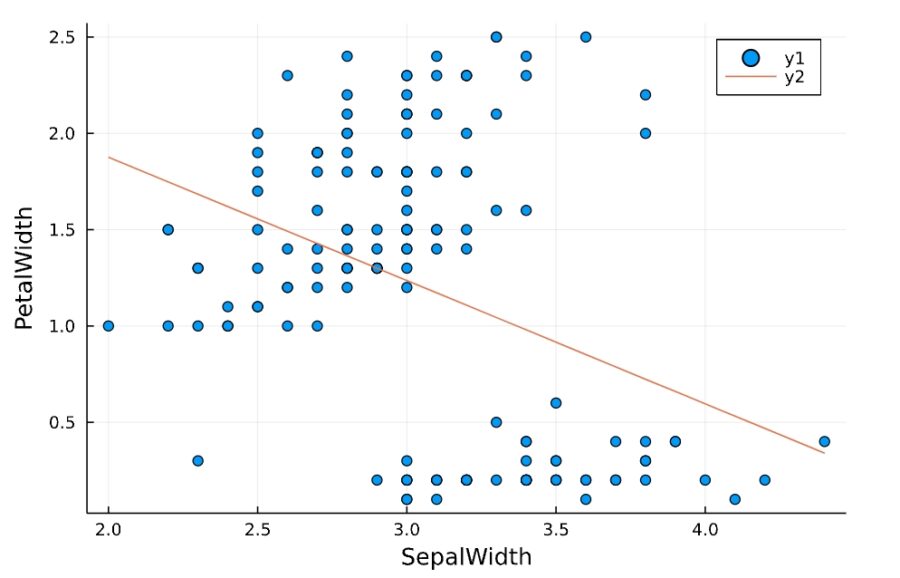
標準誤差はさきほどより大きく、回帰直線と散布図のずれを見ても、直線的な関係があるかは微妙ですね。
アイリスには品種ごとのデータがあるので、グループ分けして線形回帰してみましょう。
1 2 3 4 5 6 | iris_group=groupby(iris, :Species) for i in 1:3 display(iris_group[i][1,5]) linear_regression_plot(iris_group[i], "SepalWidth", "PetalWidth") end |
1 2 3 4 5 6 7 8 9 10 11 12 | CategoricalArrays.CategoricalValue{String, UInt8} "setosa" StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}} PetalWidth ~ 1 + SepalWidth Coefficients: ───────────────────────────────────────────────────────────────────────── Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95% ───────────────────────────────────────────────────────────────────────── (Intercept) 0.0241791 0.13458 0.18 0.8582 -0.246412 0.29477 SepalWidth 0.0647086 0.0390259 1.66 0.1038 -0.0137584 0.143175 ───────────────────────────────────────────────────────────────────────── |
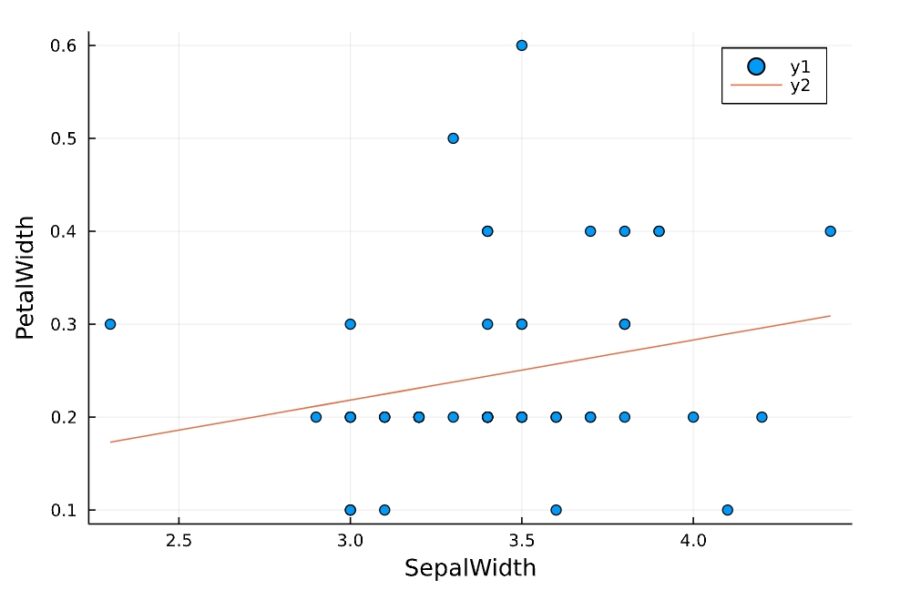
品種setosaでは、直線的な関係はなさそうです。
1 2 3 4 5 6 7 8 9 10 11 12 | CategoricalArrays.CategoricalValue{String, UInt8} "versicolor" StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}} PetalWidth ~ 1 + SepalWidth Coefficients: ─────────────────────────────────────────────────────────────────────── Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95% ─────────────────────────────────────────────────────────────────────── (Intercept) 0.166906 0.18958 0.88 0.3830 -0.21427 0.548081 SepalWidth 0.418446 0.068014 6.15 <1e-06 0.281694 0.555197 ─────────────────────────────────────────────────────────────────────── |

1 2 3 4 5 6 7 8 9 10 11 12 | CategoricalArrays.CategoricalValue{String, UInt8} "virginica" StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}} PetalWidth ~ 1 + SepalWidth Coefficients: ─────────────────────────────────────────────────────────────────────── Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95% ─────────────────────────────────────────────────────────────────────── (Intercept) 0.664059 0.309993 2.14 0.0373 0.0407774 1.28734 SepalWidth 0.457949 0.103639 4.42 <1e-04 0.249569 0.666329 ─────────────────────────────────────────────────────────────────────── |
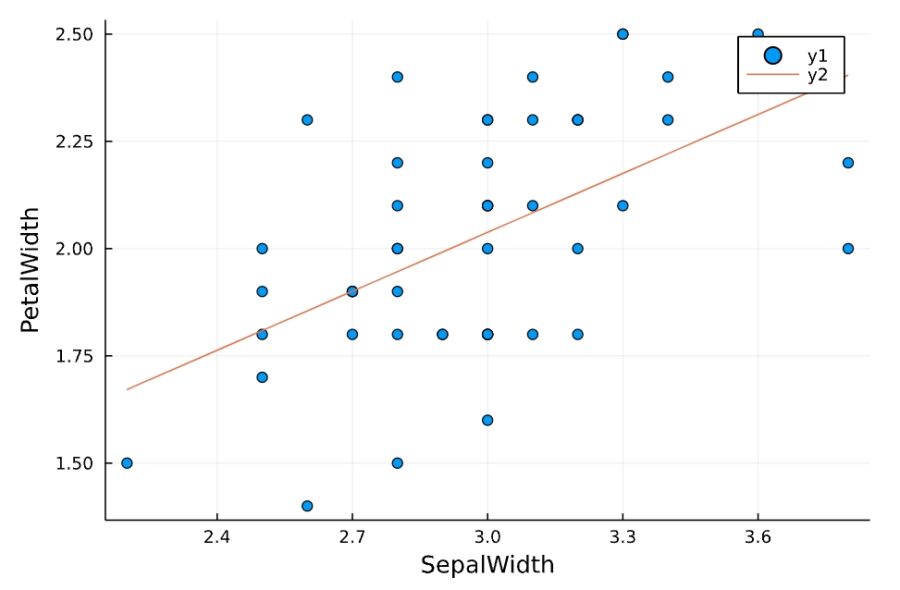
品種versicolorとvirginicaでは、がく片の長さ(SepalWidth)が長いほど花弁の長さが長い(PetalWidth)が長いという関係にあることがわかりました。
以上、Julia線形回帰、最小二乗法で回帰直線を描く方法を紹介してきました。
散布図の一覧を得るのに比べて、個別に図、回帰係数、標準誤差などが求められるのが嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Juliaでデータのヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法
最小二乗法とは:最小二乗解の求め方、正規方程式、射影による理解