どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で最大フロー問題を解き、図示する方法を紹介します。
準備
Graphs, GraphPlot, Colors, GraphsFlowsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 5 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") Pkg.add("GraphsFlows") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors, GraphsFlows |
最大フロー問題を解き、図示する方法
最大フロー問題とは
ある地点から別の地点に水や電気、物資や人を送る問題は、フローネットワークとして定式化されます。
ネットワークとは始点(ソース)と終点(シンク)のある有向グラフで、各辺にキャパシティと呼ばれる量が割り当てられています。
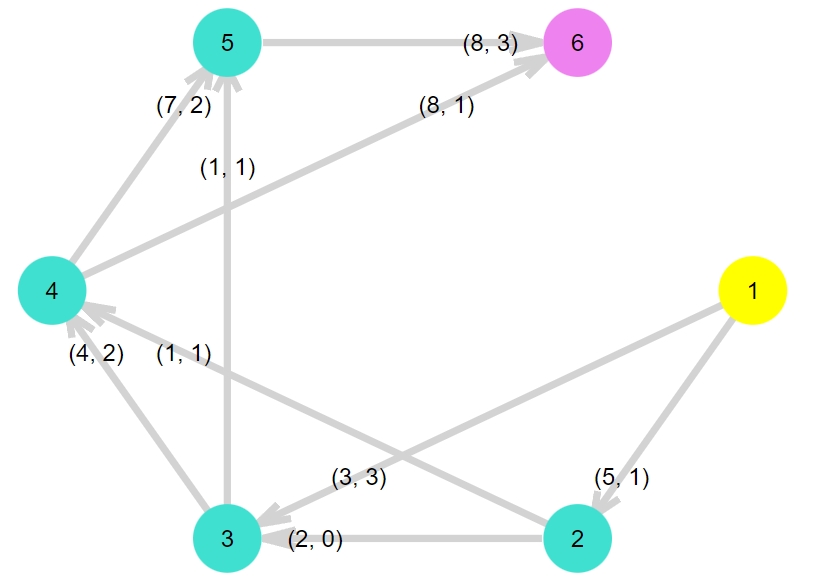
上の図は、キャパシティとフローの一例です。各辺にかかれている第1成分がキャパシティ、第2成分がフローの値です。
フローとは、キャパシティの値を超えず、各頂点で出入りする量が保存される辺の関数です。
ソースから出ていく総量を、合計フローと呼び、\(\mathrm{total }(f):= \sum_{j}f(ソース,j)\)と書きます。
与えられたネットワークに対して、フローとしては様々な可能性が考えられます。例えば、すべて0であるフロー(ゼロフロー)です。
今回考える問題は、ネットワークが与えられたとき、合計フローを最大にするようなフローを見つける問題です。これは最大フロー問題(maximum flow problem)として知られています。
応用としては、できるだけ多くの水や人を送りたい、といった問題に対応します。
簡単な例
では、簡単な例で最大フローを求めてみましょう。
まず、フローネットワークのプロットで用意した関数を導入し、さきほど示した図を得てみましょう。
1 2 3 4 5 6 | function cplot(G,source,sink,C) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" gplot(G, nodelabel= 1:nv(G), edgelabel= C, nodefillc=vcolor, layout=circular_layout) end |
1 2 3 4 5 6 7 | function cfplot(G,source,sink,C,F) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" CF = [(C[i],F[i]) for i in 1:ne(G)] gplot(G, nodelabel= 1:nv(G), edgelabel= CF, nodefillc=vcolor, layout=circular_layout) end |
1 2 3 4 5 6 7 8 9 10 11 12 | G1 = DiGraph(6) E1 = [ (1,2),(1,3),(2,3),(2,4), (3,4),(3,5),(4,5),(4,6),(5,6) ] for e in E1 Graphs.add_edge!(G1, e[1], e[2]) end C1 = [5,3,2,1,4,1,7,8,8] F1 = [1,3,0,1,2,1,2,1,3] cfplot(G1,1,6,C1,F1) |

最大フローを求める関数には、引数としてキャパシティを行列の形で与える必要があります。
キャパシティベクトルを行列に変換する関数を作りましょう。
1 2 3 4 5 6 7 8 9 | function capacity_matrix(G, capacity) size = nv(G) capacity_matrix = zeros(size,size) edges = collect(Graphs.edges(G)) for i in 1:ne(G) capacity_matrix[edges[i].src,edges[i].dst] = capacity[i] end return capacity_matrix end |
1 | CM1 = capacity_matrix(G1, C1) |
1 2 3 4 5 6 7 | 6×6 Matrix{Float64}: 0.0 5.0 3.0 0.0 0.0 0.0 0.0 0.0 2.0 1.0 0.0 0.0 0.0 0.0 0.0 4.0 1.0 0.0 0.0 0.0 0.0 0.0 7.0 8.0 0.0 0.0 0.0 0.0 0.0 8.0 0.0 0.0 0.0 0.0 0.0 0.0 |
この行列は例えば、\((1,2)\)成分=頂点1から2へ向かう辺のキャパシティが\(5.0\)であることを示しています。
「maximum_flow(グラフ,ソース,シンク,キャパシティ行列)」という関数で、与えられたネットワークの最大フローを求められます。
デフォルトでは、プッシュ・リラベル最大フローアルゴリズム(Push–relabel maximum flow algorithm)と呼ばれる方法が使われています。
第1成分が合計フロー、第2成分がフローを行列として表示したものです。
1 2 | maximum_flow(G1, 1, 6, CM1)[1] maximum_flow(G1, 1, 6, CM1)[2] |
1 2 3 4 5 6 7 8 9 | 6.0 6×6 SparseArrays.SparseMatrixCSC{Float64, Int64} with 18 stored entries: ⋅ 3.0 3.0 ⋅ ⋅ ⋅ -3.0 ⋅ 2.0 1.0 ⋅ ⋅ -3.0 -2.0 ⋅ 4.0 1.0 ⋅ ⋅ -1.0 -4.0 ⋅ 4.0 1.0 ⋅ ⋅ -1.0 -4.0 ⋅ 5.0 ⋅ ⋅ ⋅ -1.0 -5.0 ⋅ |
フローを今までと同じように図示するために、この行列をベクトルに変換しましょう。
1 2 3 4 5 6 7 8 | function flow_vector(G,M) edges = collect(Graphs.edges(G)) vector = zeros(ne(G)) for i in 1:ne(G) vector[i] = M[edges[i].src,edges[i].dst] end return vector end |
1 | MF1 = flow_vector(G1,maximum_flow(G1, 1, 6, CM1)[2]) |
1 2 3 4 5 6 7 8 9 10 | 9-element Vector{Float64}: 3.0 3.0 2.0 1.0 4.0 1.0 4.0 1.0 5.0 |
これを使えば、最大フローが図示できます。
1 | cfplot(G1,1,6,C1,MF1) |
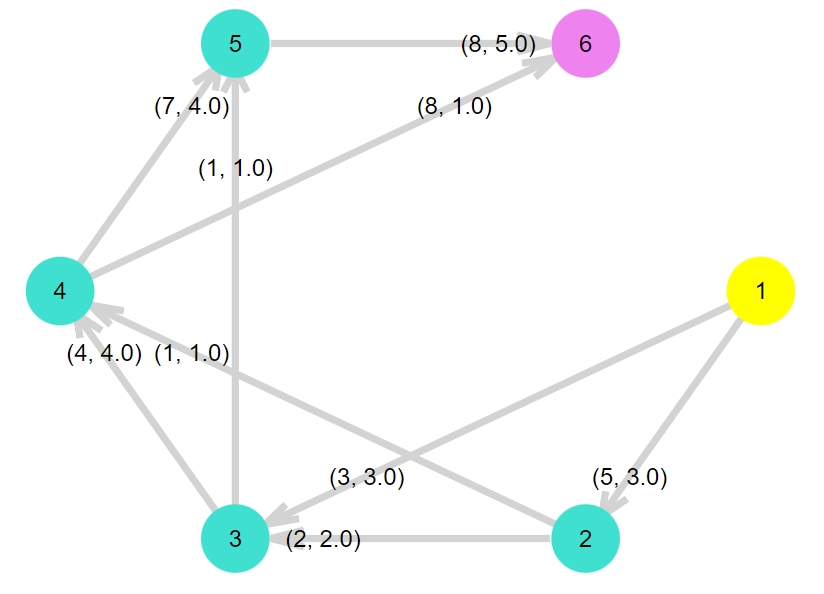
最初に図示したフロー合計は4でしたが、このフローの合計は6で、最大化されている(らしい)ことがわかりますね。
一般化
以上の結果を一般化して、ネットワークを与えたら、その最大フローの合計フローを求め、図示する関数を作りましょう。
1 2 3 4 5 6 7 | function maximum_flow_plot(G,source,sink,capacity) CM = capacity_matrix(G, capacity) total = maximum_flow(G, source, sink, CM)[1] MF = flow_vector(G,maximum_flow(G, source, sink, CM)[2]) display("合計フロー:$total") display(cfplot(G,source,sink,capacity,MF)) end |
別の例として、次のネットワークを考えます。
1 2 3 4 5 6 7 8 9 10 | G2 = DiGraph(7) E2 = [ (1,2),(1,4),(2,3),(3,7),(4,5), (5,2),(5,3),(5,6),(6,3),(6,7) ] for e in E2 Graphs.add_edge!(G2, e[1], e[2]) end C2 = [8,7,8,10,6,6,4,4,2,6] cplot(G2,1,7,C2) |
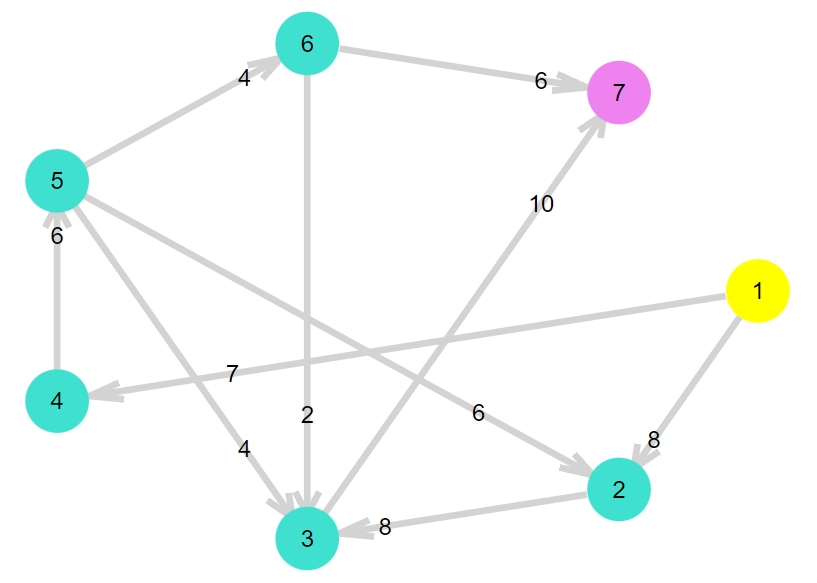
さきほどの関数を使えば、最大フローが簡単に求められます。
1 | maximum_flow_plot(G2,1,7,C2) |
1 | "合計フロー:14.0" |

以上、Julia(Graphs)で最大フロー問題を解き、図示する方法を紹介してきました。
与えられたネットワークのフローの候補はたくさんあるので、手計算で求めるのは、不可能ではありませんが大変です。
最大フロー問題を解くアルゴリズムはいくつかありますが、それを学ぶにあたっても、まずは今回のように具体的に問題を解いてみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法