どうも、木村(@kimu3_slime)です。
今回は、フローネットワークとは何か、Julia(Graphs)で図示する方法を紹介します。
前提知識:グラフ理論入門:グラフとは、グラフの同型、Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法
フローネットワークとは
ある出発点から別の終点に、水や電気、情報や物資や人を効率よく送りたい。そんな問題(輸送問題)を考えるとき、フローネットワーク(flow network)の考え方が役に立ちます。
例えば、ある地域で災害があったときに、できるだけ多くの人が速く安全な地点まで避難したい。そんなときに、どの道をどのくらいの人が通れば良いか。その問題は、最速避難計画問題と呼ばれています。
参考:最速避難計画のモデリングと解法 – 日本オペレーションズ・リサーチ
フローネットワークは、グラフ理論によって定式化されます。
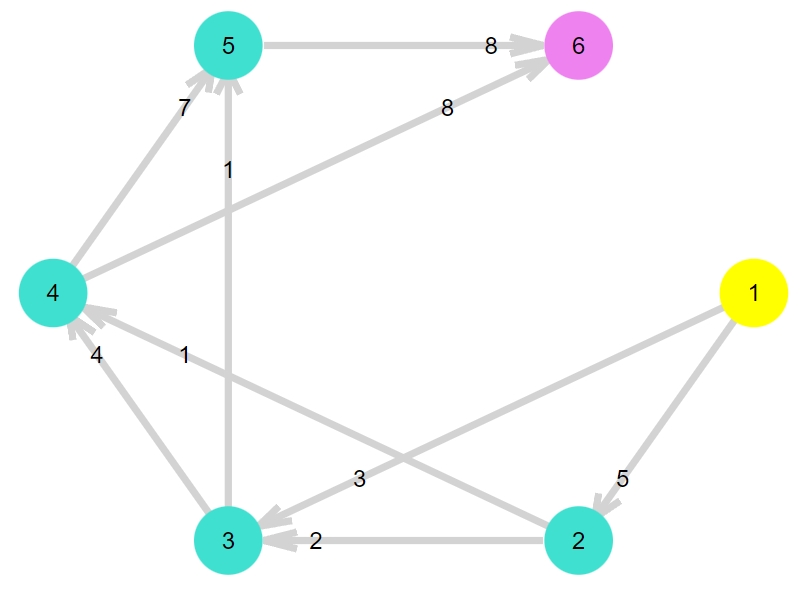
まず、辺に向きのあるグラフ(有向グラフ)\(G=(V,E)\)を考えましょう。そこに区別される2つの頂点、出発点と終点、ソース(source)とシンク(sink)があります。ソースを黄色に、シンクを紫色にしました。
各辺にかかれている数字は、人や水が通れる限界量を示しています。一般に、各辺に対して非負の値を対応させる関数\(c: E \to [0,\infty)\)をキャパシティ(capacity)、容量と呼びます。上の図の例ならば、例えば\(c(1,2)=5\)、\(c(2,3)=2\)です。
そして、有向グラフ、ソース、シンク、キャパシティの組をまとめて、ネットワーク(network)と呼びます。
ネットワークの上を、水が流れたり、人が通ったりする状況を表しましょう。
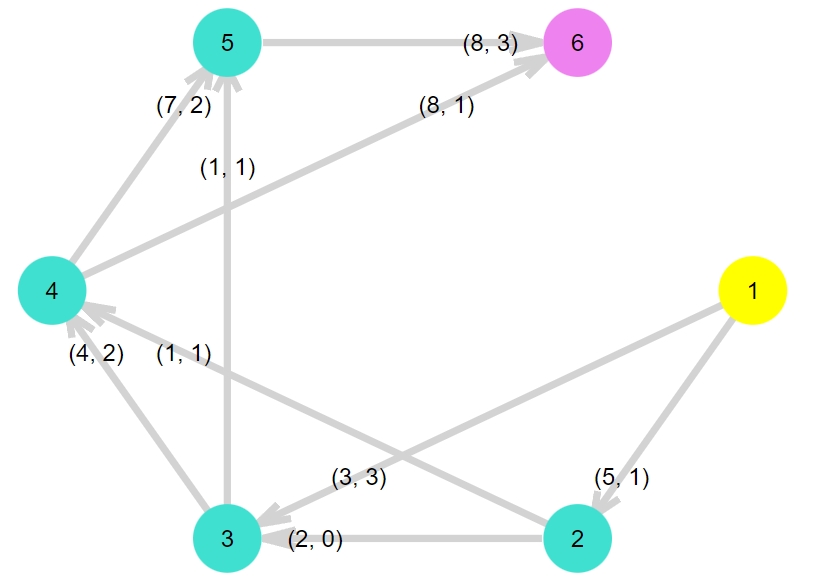
辺の上に書かれている数字が増えました。第1成分がキャパシティ、第2成分が流れている量:フローです。
(実行可能な)フロー(flow)とは、辺に対し非負値を割り当てる関数\(f: E \to [0,\infty)\)で、
- キャパシティ条件:すべての辺\((i,j) \in E\)に対し、\(f(i,j) \leq c(i,j)\)
- 量の保存:ソースとシンク以外のすべての頂点\(i \in V\)に対し、入ってくるフロー(inflow)と出ていくフロー(outflow)が等しい。
- \(\sum_{k}f(k,i) = \sum_{j} f(i,j)\)
- 量の保存:\(\sum_{j}f(ソース,j) = \sum_{k} f(k,シンク)\)
を満たすものです。
上の図の辺に書かれた情報\((c,f)\)を見て、フローの条件を満たすことをチェックしてみてください。(慣習によっては、\((c,f)\)ではなく\(f/c\)と逆の順序で書かれていることもあります。)
まず、右側の数字は左側の数字を超えません。キャパシティ以上にフローを流すことはできないわけです。
そして、途中の頂点では、入ってくるフローと出ていくフローが必ず等しいです。どこかに漏れてしまったりはしないと仮定しているわけですね。頂点\(4\)に注目すれば、入ってくるフローの合計は\(f(2,4)+f(3,4)=1+2=3\)、出ていくフローの合計は\(f(4,5)+f(4,6)=2+1=3\)と等しいです。他の頂点でもチェックしてみてください。
さらに、ソースから出ていくフローとシンクが受け取るフローは等しいです。\(f(1,2)+f(1,3)=1+3=4\)、\(f(4,6)+f(5,6)=4\)ですね。
ソースから出ていく総量を、合計フロー(total flow)、フローの値(value of flow)と呼びます。つまり、\(\mathrm{total }(f):= \sum_{j}f(ソース,j)\)です。この値を、単にフローと呼んでいることもあるので注意。
与えられたネットワークに対して、フローとしては様々な可能性が考えられます。
例えば、すべての辺に何も流さない\(f(i,j)=0\)はフローの定義を満たしますね(チェックしてみてください)。これをゼロフローと呼びます。

ただし、何も流れないフローを考えたのでは、役に立ちそうにありませんね。
例えば、できるだけ多くの水や人を送りたい、つまり合計フローを最大化するフローを求めることはできないでしょうか。これは最大フロー問題として知られています。別記事で紹介予定。
Juliaで図示する方法
フローとネットワークの考え方を一通り知ったところで、使ってきた図をJuliaで描く方法を紹介します。
準備
Graphs, GraphPlot, Colorsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
簡単な例
まず、次のような有向グラフを考えましょう。
1 2 3 4 5 6 7 8 9 | G1 = DiGraph(6) E1 = [ (1,2),(1,3),(2,3),(2,4), (3,4),(3,5),(4,5),(4,6),(5,6) ] for e in E1 Graphs.add_edge!(G1, e[1], e[2]) end G1 |
1 | {6, 9} directed simple Int64 graph |
「DiGraph(6)」で6頂点で(辺のない)有向グラフを作成。その後、辺の候補を作って、「Graphs.add_edge!」で辺を追加しました。
各辺に対するキャパシティは、キャパシティベクトルとして与えられます。
1 | C1 = [5,3,2,1,4,1,7,8,8] |
また、ソースとシンクを色を変えて図示しましょう。次のように色のベクトルが作れます。
1 2 3 4 | vcolor1 = [colorant"turquoise" for i in 1:nv(G1)] vcolor1[1] = colorant"yellow" vcolor1[6] = colorant"violet" vcolor1 |

以上の情報を使って、グラフをプロットしましょう。辺の上に描く数字をキャパシティベクトル、頂点の色を指定しています。
1 | gplot(G1, nodelabel= 1:nv(G1), edgelabel= C1, nodefillc=vcolor1, layout=circular_layout) |

さらに、フローの具体例も図示しましょう。
フローもキャパシティと同様に、フローベクトルとして与えられます。
キャパシティとベクトルの組を作って、それを使って辺のラベルを描きましょう。
1 2 3 | F1 = [1,3,0,1,2,1,2,1,3] CF1 = [(C1[i],F1[i]) for i in 1:ne(G1)] gplot(G1, nodelabel= 1:nv(G1), edgelabel= CF1, nodefillc=vcolor1, layout=circular_layout) |

関数による一般化
今までの結果を一般化したのが、次の関数です。
1 2 3 4 5 6 | function cplot(G,source,sink,C) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" gplot(G, nodelabel= 1:nv(G), edgelabel= C, nodefillc=vcolor, layout=circular_layout) end |
1 2 3 4 5 6 7 | function cfplot(G,source,sink,C,F) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" CF = [(C[i],F[i]) for i in 1:ne(G)] gplot(G, nodelabel= 1:nv(G), edgelabel= CF, nodefillc=vcolor, layout=circular_layout) end |
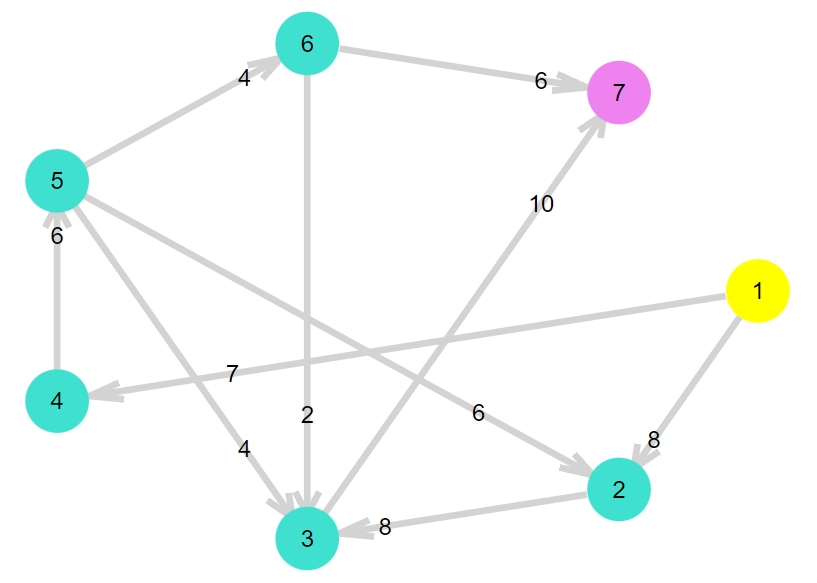
別のネットワーク、フローを考えて、関数で図示してみましょう。
1 2 3 4 5 6 7 8 9 10 11 | G2 = DiGraph(7) E2 = [ (1,2),(1,4),(2,3),(3,7),(4,5), (5,2),(5,3),(5,6),(6,3),(6,7) ] for e in E2 Graphs.add_edge!(G2, e[1], e[2]) end C2 = [8,7,8,10,6,6,4,4,2,6] F2 = [4,5,5,8,5,1,2,2,1,1] |
1 | cplot(G2,1,7,C2) |
1 | cfplot(G2,1,7,C2,F2) |
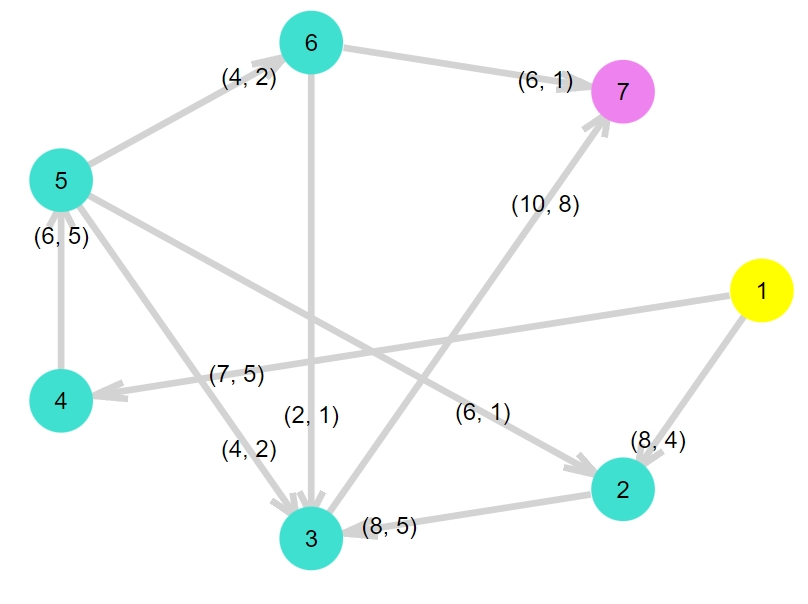
うまくプロットできていますね。
以上、フローネットワークとは何か、Julia(Graphs)で図示する方法を紹介してきました。
輸送に関する問題が、フローネットワークによって定式化できるのがわかりました。最大フロー問題については、別記事で紹介します。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法