どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で重み付きグラフの最小全域木を求め、図示する方法を紹介します。
前提知識:Julia(Graphs)で最小全域木を求め、図示する方法
準備
Graphs, GraphPlot, Colors, Randomを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors, Random |
最小全域木を求め、図示する方法
最小全域木とは
まず、与えられたグラフ\(G\)の全域木(spanning tree)とは、すべての頂点を保ったまま、辺を部分的に取り除くことで得る木(グラフ)のことです。木(tree)とは、連結であり、サイクルを持たないグラフでした。
一般に、グラフの全域木にはいくつかの候補があります。重み付きグラフを考えて、その中で辺の重みの合計が最も少ないものを、最小全域木(minimum spanning tree; MST)と呼びます。
この問題は、送電網やネットワークの効率化に応用できるものです。
簡単な例と関数作り
次の簡単な重み付きグラフを考えましょう。
1 2 3 4 | G1 = smallgraph(:diamond) Random.seed!(2022) weights1 = rand(1:5, ne(G1)) gplot(G1, nodelabel= 1:nv(G1), edgelabel= weights1) |
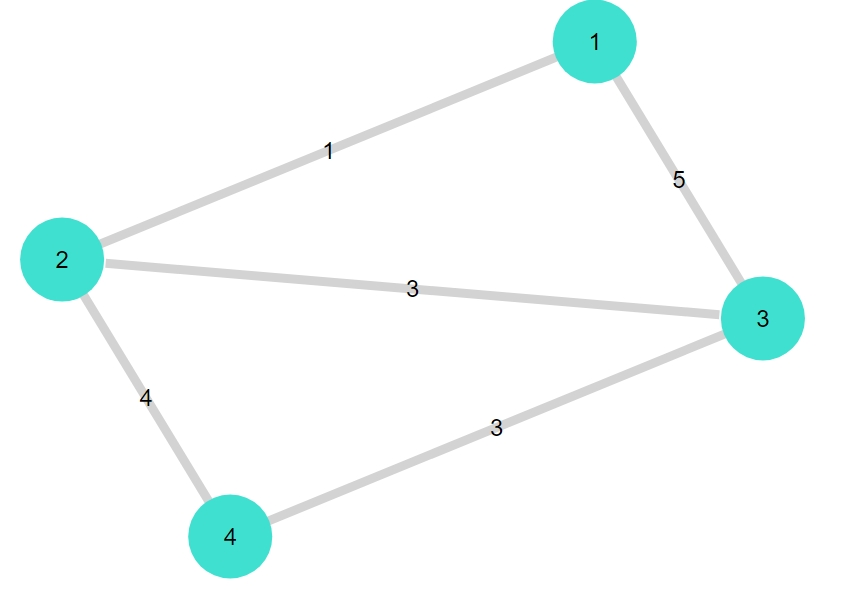
重みベクトルによって、各辺に重みを指定しています。
今回は、1以上5以下の整数をランダムに与えました。乱数のシードを指定することで、実行結果は再現されます。
最小全域木を求めるためには、重みベクトルを距離行列に変換する必要があります。
1 2 3 4 5 6 7 8 | function distance_matrix(g, weights) D = zeros(Int,(nv(g),nv(g))) for i in 1:length(weights) D[collect(edges(g))[i].src,collect(edges(g))[i].dst] = weights[i] D[collect(edges(g))[i].dst,collect(edges(g))[i].src] = weights[i] end return D end |
例えば、今回与えた距離行列は、次のようなものです。
1 | D1 = distance_matrix(G1, weights1) |
1 2 3 4 5 | 4×4 Matrix{Float64}: 0.0 1.0 5.0 0.0 1.0 0.0 3.0 4.0 5.0 3.0 0.0 3.0 0.0 4.0 3.0 0.0 |
「kruskal_mst(グラフ, 距離行列)」で、重み付きグラフの最小全域木がクラスカル法によって求められます。
辺をすべて取り除いたグラフに、サイクルが作られないようにひとつずつ辺を加えていく方法です。辺を加える順序として、重みが小さい順に並べ替えておきます。
1 | kruskal_mst(G1, D1) |
1 2 3 4 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 3 Edge 3 => 4 |
求められた最小全域木の重み合計を計算する関数を作りましょう。
1 2 3 4 5 6 7 8 9 | function mst_weight_sum(g,weights) D = distance_matrix(g, weights) E = kruskal_mst(g, D) weight_sum = 0 for e in E weight_sum += D[e.src, e.dst] end return weight_sum end |
1 | mst_weight_sum(G1, weights1) |
1 | 7 |
以上の結果をまとめて、最短経路問題と同様にして図示してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | function mst_plot(g, weights) D = distance_matrix(g, weights) mst = kruskal_mst(g, D) weight_sum = mst_weight_sum(g, weights) display(mst) display("重み合計:$weight_sum") colors = [colorant"lightgrey" for i in 1:ne(g)] for e in mst if isnothing(indexin([e],collect(edges(g)))[1]) != true (colors[indexin([e],collect(edges(g)))[1]] = colorant"orange" ) elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true (colors[indexin([reverse(e)],collect(edges(g)))[1]] = colorant"orange" ) end end display(gplot(g, nodelabel= 1:nv(g), edgelabel= weights, edgestrokec=colors )) end |
1 | mst_plot(G1, weights1) |
1 2 3 4 5 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 3 Edge 3 => 4 "重み合計:7" |
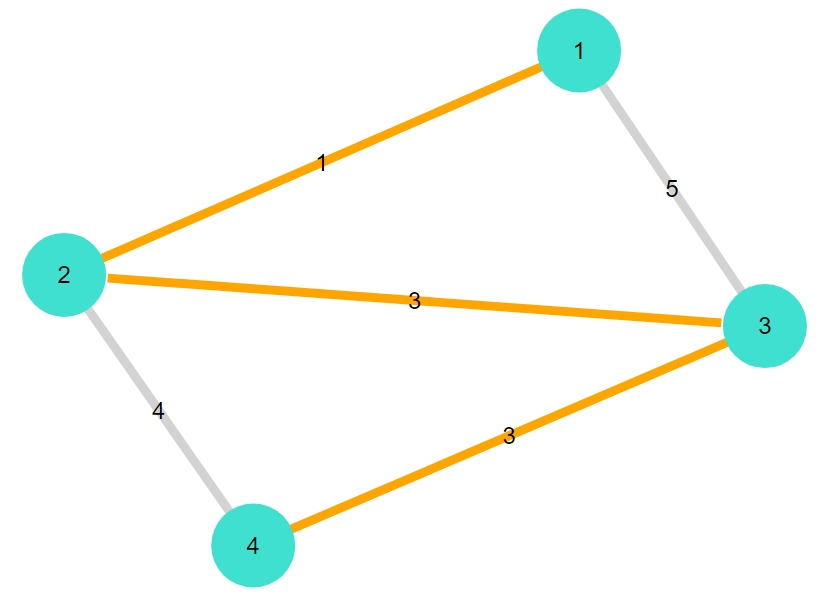
このグラフには他にも全域木がありますが、それと比べても辺の重み合計が最小となっていることがわかりますね。どの辺を1つ付け替えても、必ず重みの合計は増えてしまいます。
正多面体グラフの最小全域木
Graphs.jlでは、smallgraphという関数でプラトン立体のグラフが作れます。
辺に1から5までのランダムな整数の重みを与え、最小全域木を求めてみましょう。
1 2 3 4 5 6 | Random.seed!(2022) Platonic_solid = [:tetrahedral, :cubical, :octahedral, :dodecahedral, :icosahedral] @time for s in Platonic_solid display("$s") mst_plot(smallgraph(s),rand(1:5, ne(smallgraph(s)))) end |
正四面体
1 2 3 4 5 6 | "tetrahedral" 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 4 Edge 2 => 3 "重み合計:8" |

正六面体(立方体)
1 2 3 4 5 6 7 8 9 10 | "cubical" 7-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 4 Edge 2 => 3 Edge 3 => 7 Edge 5 => 6 Edge 2 => 8 Edge 1 => 2 Edge 1 => 5 "重み合計:19" |

正八面体
1 2 3 4 5 6 7 8 | "octahedral" 5-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 2 => 3 Edge 2 => 6 Edge 4 => 5 Edge 4 => 6 Edge 1 => 2 "重み合計:8" |

正十二面体
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | "dodecahedral" 19-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 11 Edge 2 => 9 Edge 3 => 4 Edge 5 => 18 Edge 6 => 16 Edge 10 => 14 Edge 19 => 20 Edge 7 => 8 Edge 8 => 9 Edge 8 => 15 Edge 12 => 19 Edge 15 => 16 Edge 5 => 6 Edge 9 => 10 Edge 11 => 12 Edge 17 => 18 Edge 2 => 3 Edge 12 => 13 "重み合計:38" |
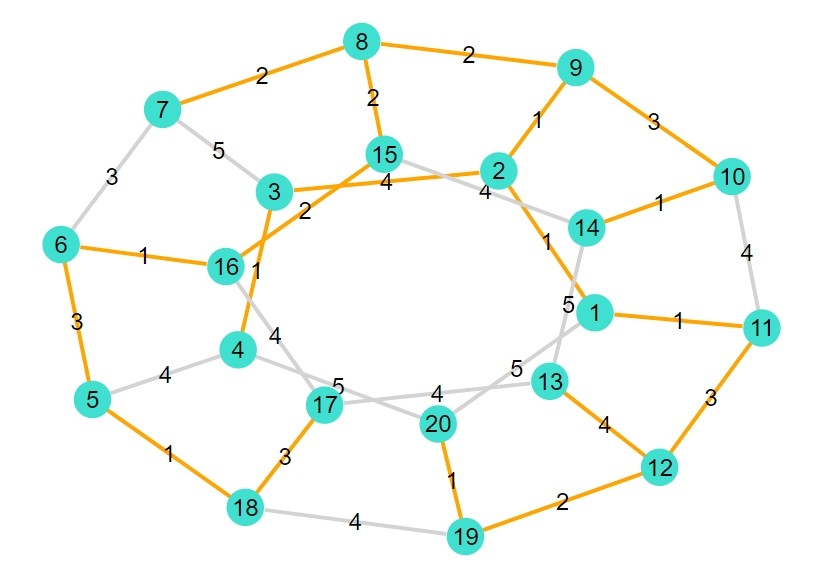
正二十面体
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | "icosahedral" 11-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 12 Edge 4 => 7 Edge 5 => 12 Edge 6 => 7 Edge 8 => 11 Edge 2 => 6 Edge 3 => 7 Edge 5 => 7 Edge 5 => 11 Edge 8 => 9 Edge 8 => 10 "重み合計:17" |

以上、Julia(Graphs)で最小全域木を求め、図示する方法を紹介してきました。
プラトン立体の結果をすべて表示するのに1秒かからず、目で見てわかるグラフが得られるのは便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
重み付きグラフ、最小全域木の問題とは? クラスカル法による解き方
Julia(Graphs)で最短経路問題を解き、図示する方法