どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)でハミルトンサイクルを求め、図示する方法を紹介します。
前提知識:グラフ理論における経路、連結性とは?、Julia(Graphs)で最短経路問題を解き、図示する方法
目次
準備
Graphs, GraphPlot, Colorsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
ハミルトンサイクルを求め、図示する方法
ハミルトンサイクルとは
ハミルトンサイクル(Hamiltonian cycle)は、与えられたグラフのすべての頂点を一度だけ通るようなサイクル(単純な閉経路)です。ハミルトン閉路とも。
ハミルトンサイクルはいつでも存在するとは限りませんが、存在するときはグラフはハミルトングラフ(Hamiltonian graph)と呼ばれます。
重みつきグラフにおいて、その重さの合計を最小化するようなハミルトン経路を探す問題は、巡回セールスマン問題(traveling salesman problem)と呼ばれる有名な問題です。
目標とする複数の都市すべてを巡回したいセールスマンが、都市間の重み、例えば移動距離を最小化したい、という問題ですね。
巡回セールスマン問題において各辺の重みがすべて等しいケースがハミルトンサイクルを求める問題であり、ハミルトンサイクル問題の一般化が巡回セールスマン問題です。
ハミルトンサイクルの求め方
では、Juliaを使って具体的にハミルトンサイクルを求める方法を紹介しましょう。
まず、「simplecycles_limited_length(グラフ, n))」で、グラフに含まれる長さn以下の単純な(=頂点の重複がない)サイクル(正確には閉経路)がすべて求められます。
ハミルトンサイクルの長さはグラフの頂点数に等しいので、最大値として「nv(グラフ)」を指定しましょう。
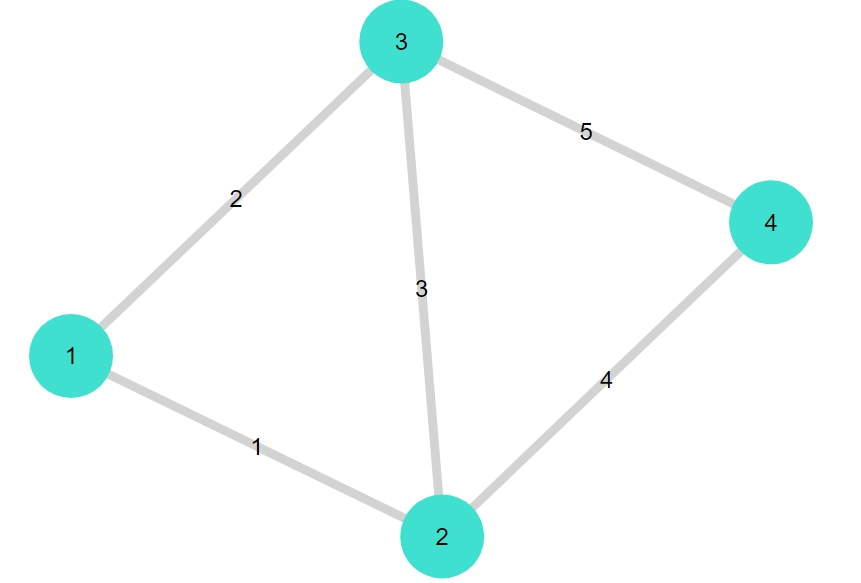
1 2 3 | G1 = smallgraph(:diamond) gplot(G1, nodelabel= 1:nv(G1), edgelabel= 1:ne(G1)) simplecycles_limited_length(G1, nv(G1)) |
1 | {4, 5} undirected simple Int64 graph |
1 2 3 4 5 6 7 8 9 10 11 12 | 11-element Vector{Vector{Int64}}: [1, 2] [1, 2, 3] [1, 2, 4, 3] [1, 3] [1, 3, 2] [1, 3, 4, 2] [2, 3] [2, 3, 4] [2, 4] [2, 4, 3] [3, 4] |
長さ4以下のサイクルがすべて求められています。このうち、すべての頂点を通るサイクル、ハミルトンサイクルは、[1, 2, 4, 3]と[1, 3, 4, 2]ですね。
グラフのハミルトンサイクルを求める関数を作りましょう。
1 2 3 4 5 6 7 8 9 | function Hamiltonian_cycle(g) for c in simplecycles_limited_length(g, nv(g)) if length(c) == nv(g) && length(c) >= 3 return c else end end return [] end |
サイクルであって、その長さがグラフの頂点数に等しいものがあればそれがハミルトンサイクルなので、それを戻り値にします。
長さが2のものは閉経路ではありますが、サイクルとは呼びません。長さ3以上のものがないときは、空の配列を返す仕様です。
1 | Hamiltonian_cycle(G1) |
1 2 3 4 5 | 4-element Vector{Int64}: 1 2 4 3 |
ハミルトンサイクルのひとつが求められました。
ハミルトンサイクルの図示
ハミルトンサイクルをよりわかりやすく理解するため、辺に色をつけたプロットによって図示しましょう。
そのために、Hamiltonian_cycleの数ベクトルを、SimpleEdge型のベクトルに変換します。空のグラフにHamiltonian_cycleの情報を使って辺を加えていき、collect(edges(GE))で辺をまとめます。
1 2 3 4 5 6 7 | GE = SimpleGraph(nv(G1)) for i in 1:length(Hamiltonian_cycle(G1))-1 add_edge!(GE, Hamiltonian_cycle(G1)[i], Hamiltonian_cycle(G1)[i+1]) end add_edge!(GE, Hamiltonian_cycle(G1)[length(Hamiltonian_cycle(G1))], Hamiltonian_cycle(G1)[1]) GE collect(edges(GE)) |
1 2 3 4 5 6 7 | {4, 4} undirected simple Int64 graph 4-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 4 Edge 3 => 4 |
辺(SimpleEdge)のベクトルを使えば、最短経路問題と同様にして、辺に色をつけてプロットできます。
1 2 3 4 5 6 7 8 | colors = [colorant"lightgrey" for i in 1:ne(G1)] for e in collect(edges(GE)) (colors[indexin([e],collect(edges(G1)))[1]] = colorant"orange" ) end colors gplot(G1,nodelabel= 1:nv(G1), edgelabel= 1:ne(G1), edgestrokec=colors ) |

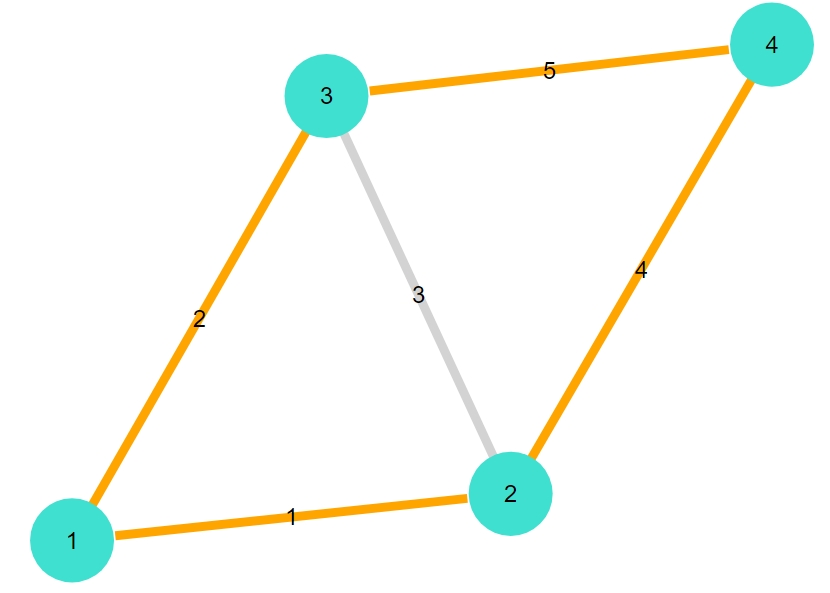
ハミルトンサイクルが一目瞭然ですね。
一般形
以上の結果を一般化して、ハミルトンサイクルを求め、それを図示する関数を作りましょう。「Hamiltonian_cycle」の長さが3以上ならプロットし、それ以下ならば「ハミルトンサイクルは存在しない」と表示することにします。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | function Hamiltonian_cycle_plot(g) if length(Hamiltonian_cycle(g)) >= 3 GE = SimpleGraph(nv(g)) for i in 1:length(Hamiltonian_cycle(g))-1 add_edge!(GE, Hamiltonian_cycle(g)[i], Hamiltonian_cycle(g)[i+1]) end add_edge!(GE, Hamiltonian_cycle(g)[length(Hamiltonian_cycle(g))], Hamiltonian_cycle(g)[1]) display(collect(edges(GE))) colors = [colorant"lightgrey" for i in 1:ne(g)] for e in collect(edges(GE)) if isnothing(indexin([e],collect(edges(g)))[1]) != true (colors[indexin([e],collect(edges(g)))[1]] = colorant"orange" ) elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true (colors[indexin([reverse(e)],collect(edges(g)))[1]] = colorant"orange" ) end end display(gplot(g, nodelabel= 1:nv(g), edgelabel= 1:ne(g), edgestrokec=colors)) else println("ハミルトンサイクルは存在しない") end end |
ハミルトンサイクルが存在しない例
ケーニヒスベルクの橋のグラフについて調べてみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | G2 = smallgraph(:diamond) add_vertices!(G2,4) add_edge!(G2 , 1, 5) add_edge!(G2 , 1, 6) add_edge!(G2 , 2, 5) add_edge!(G2 , 2, 6) add_edge!(G2 , 2, 7) add_edge!(G2 , 2, 8) add_edge!(G2 , 4, 7) add_edge!(G2 , 4, 8) rem_edge!(G2 , 1, 2) rem_edge!(G2 , 2, 4) G2 gplot(G2,nodelabel= 1:nv(G2), edgelabel= 1:ne(G2)) |
1 | {8, 11} undirected simple Int64 graph |
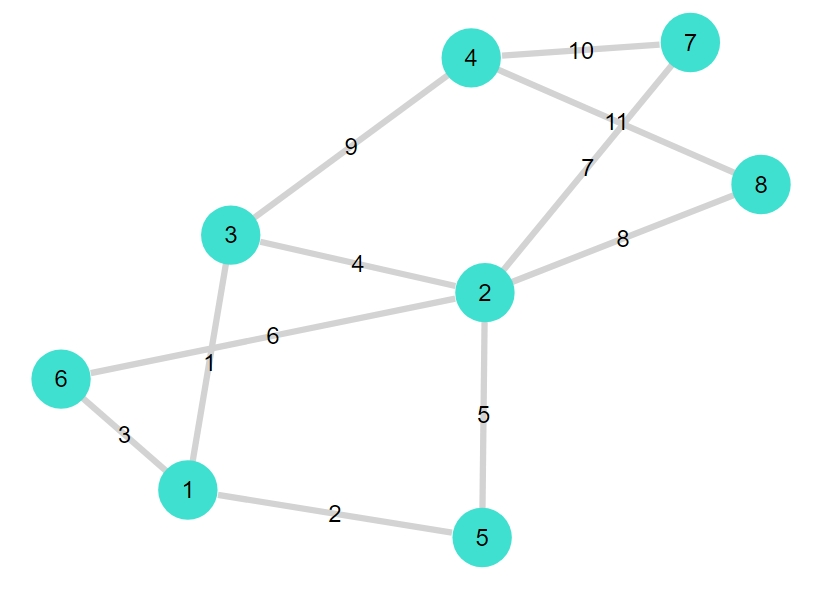
1 | Hamiltonian_cycle_plot(G2) |
1 | ハミルトンサイクルは存在しない |
このグラフがハミルトングラフでないことがわかりました。
正多面体グラフのハミルトンサイクル
プラトン立体(正多面体)のグラフは、すべてハミルトングラフであることが知られています。それを確かめてみましょう。
Graphs.jlでは、smallgraphという関数でプラトン立体のグラフが作れます。
1 2 3 4 | Platonic_solid = [:tetrahedral, :cubical, :octahedral, :dodecahedral, :icosahedral] for s in Platonic_solid Hamiltonian_cycle_plot(smallgraph(s)) end |
正四面体
1 2 3 4 5 | 4-element Vector{Int64}: 1 2 3 4 |
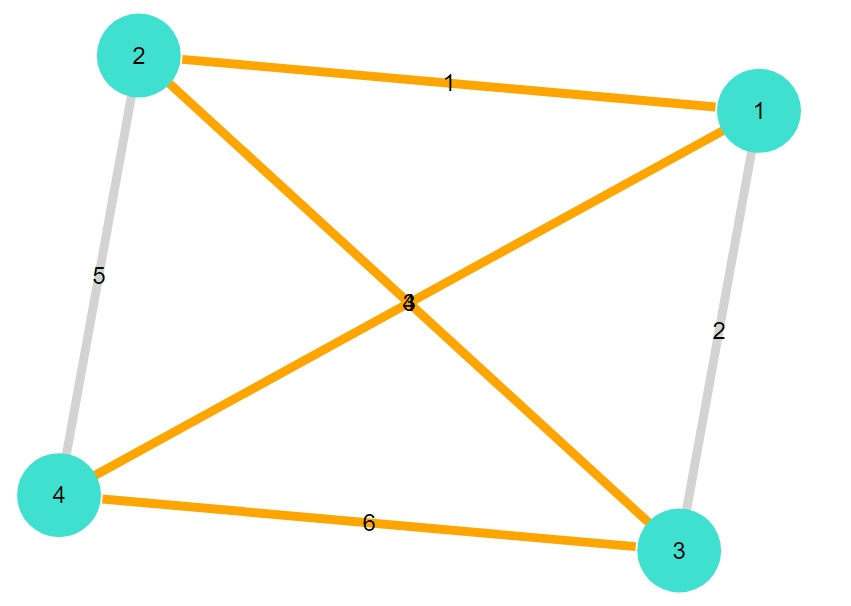
正六面体(立方体)
1 2 3 4 5 6 7 8 9 | 8-element Vector{Int64}: 1 2 3 4 6 7 8 5 |
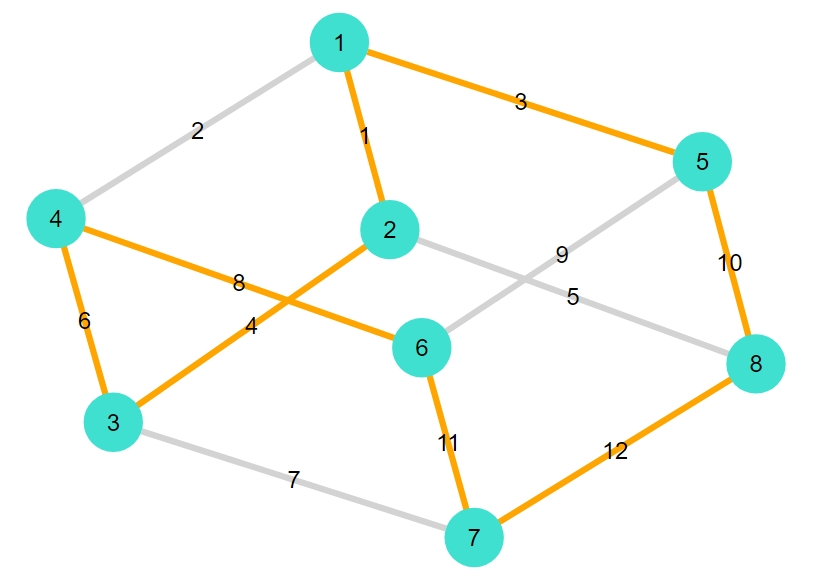
正八面体
1 2 3 4 5 6 7 | 6-element Vector{Int64}: 1 2 3 5 6 4 |
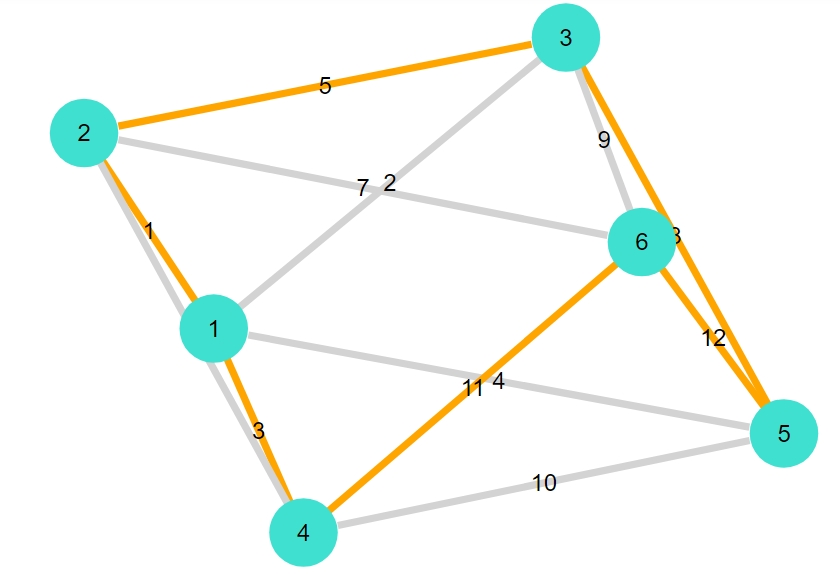
正十二面体
これは、数学者のハミルトンがハミルトンサイクル問題を最初に考えた例と言われています。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | 20-element Vector{Int64}: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
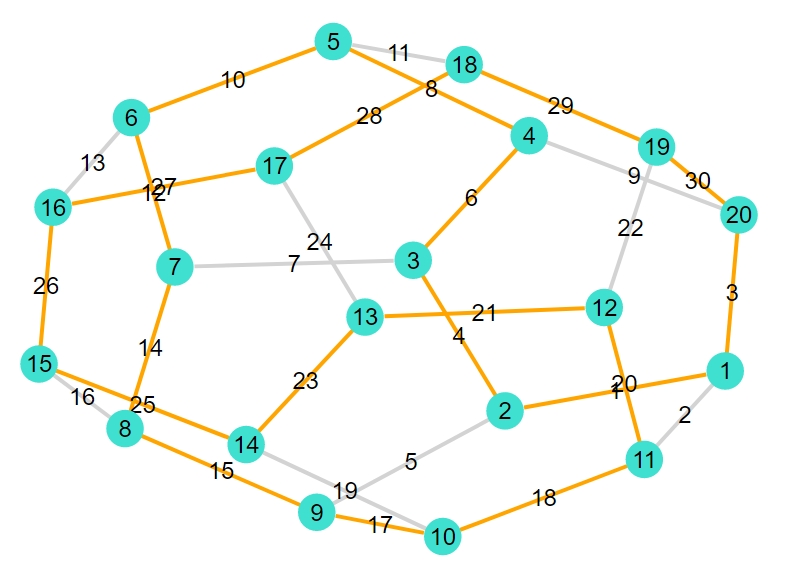
正二十面体
1 2 3 4 5 6 7 8 9 10 11 12 13 | 12-element Vector{Int64}: 1 2 3 4 5 7 6 12 8 11 10 9 |

以上、Julia(Graphs)でハミルトンサイクルを求め、図示する方法を紹介してきました。
ハミルトンサイクルが存在するかどうかを決定する一般的な問題は、グラフのサイズが大きくなると時間がかかります。計算複雑性の理論では、ハミルトンサイクル問題はNP完全、巡回セールスマン問題はNP困難です。
実際、頂点数50、辺の数1000を持つあるグラフのsimplecycles_limited_lengthを実行すると、約2秒かかる上に、サイクルの一部しか求められていません。simplecycles_limited_lengthで求められるサイクルの数の上限は、10^6=100万です。(より速く、サイズの大きな問題に適した方法があるかもしれません。)
それでも、プラトン立体のグラフ程度の問題ならば、合計で1秒程度で図示もできるので、ぜひ試してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)で最短経路問題を解き、図示する方法
重み付きグラフ、最小全域木の問題とは? クラスカル法による解き方