どうも、木村(@kimu3_slime)です。
今回は、Julia(JuMP,GLPK)で線形計画法の問題を解く方法を紹介します。
準備
JuMP、GLPKを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("JuMP") Pkg.add("GLPK") |
準備として、以下のコードを実行しておきます。
1 | using JuMP, GLPK |
線形計画法の問題を解く方法
例として、飲み物の生産量の最適化問題を考えましょう。
変数は\(x_1,x_2,x_3\geq 0\)
最小化したい目的関数は\(f(x)= x_1 + 2x_2 + 3 x_3\)
制約条件は\(x_1 + x_2 + x_3 =10\)、\(5 x_1 + x_3 =20\)とします。
これをJuliaでモデル化してみましょう。
1 2 3 4 5 6 | model = Model(GLPK.Optimizer) @variable(model, x[i=1:3] >= 0) @objective(model, Min, x[1] + 2*x[2] + 3*x[3]) @constraint(model, c1, x[1] + x[2] + x[3] == 10) @constraint(model, c2, 5*x[1] + x[3] == 20) |
まず、「Model」によって線形計画法の空のモデルを作ります。これに変数、目的関数、制約条件を足していきましょう。カッコの中身「GLPK.Optimizer」は、GLPKを使って最適化することを意味したものです。
「@variable(model, 変数と仮定)」で変数\(x_1,x_2,x_3\)を追加します。条件「>=0」は、非負の値であるとの仮定です。
「@objective(model, Min,関数)」によって、目的関数が追加できます。Minならば最小化、Maxならば最大化です。
「@constraint(model, 条件名, 制約条件)」で制約条件の追加です。等号の条件は「==」とイコールが2つになることに注意しましょう。
「print(model)」で、これまでモデルに追加してきた内容が確認できます。
1 | print(model) |
1 2 3 4 5 6 7 | Min x[1] + 2 x[2] + 3 x[3] Subject to c1 : x[1] + x[2] + x[3] == 10.0 c2 : 5 x[1] + x[3] == 20.0 x[1] >= 0.0 x[2] >= 0.0 x[3] >= 0.0 |
さて、このモデルを解いてみましょう。
1 2 | optimize!(model) termination_status(model) |
1 | OPTIMAL::TerminationStatusCode = 1 |
「optimize!(model)」で最適化が実行されます。結果はそのままでは表示されません。
「termination_status(model)」で最適化の結果が表示されます。今回は「OPTIMAL」、つまり最適解に達しました。
「value(変数)」で最適解の値、「objective_value(model)」でそのときの目的関数の値が求められます。
1 2 | value(x[1]), value(x[2]), value(x[3]) objective_value(model) |
1 2 | (4.0, 6.0, 0.0) 16.0 |
きちんと解けました。
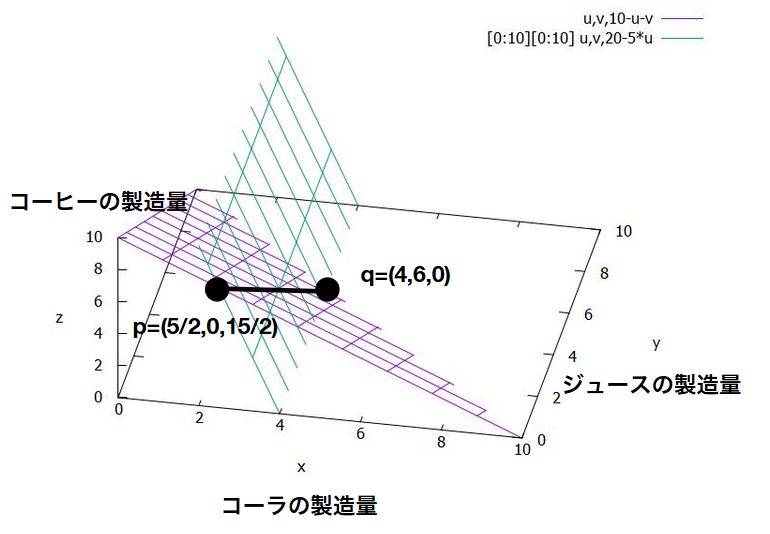
もうひとつ、別の線形計画問題を解いてみましょう。目的関数の最大化と、不等式の制約条件を課してみます。
変数は\(x_1,x_2,x_3\geq 0\)
最大化したい目的関数は\(f(x)= 2x_1 + 3x_2 + x_3\)
制約条件は\(x_1 + x_2 + x_3 \leq 4.8\)、\(10 x_1 + x_3 \leq 9.9\)、\(x_2 -x_3 \leq 0.2\)とします。
1 2 3 4 5 6 7 8 9 | model2 = Model(GLPK.Optimizer) @variable(model2, x[i=1:3] >= 0) @objective(model2, Max, 2*x[1] + 3*x[2] + x[3]) @constraint(model2, c1, x[1] + x[2] + x[3] <= 4.8) @constraint(model2, c2, 10*x[1] + x[3] <= 9.9) @constraint(model2, c3, x[2] - x[3] <= 0.2) print(model2) |
1 2 3 4 5 6 7 8 | Max 2 x[1] + 3 x[2] + x[3] Subject to c1 : x[1] + x[2] + x[3] <= 4.8 c2 : 10 x[1] + x[3] <= 9.9 c3 : x[2] - x[3] <= 0.2 x[1] >= 0.0 x[2] >= 0.0 x[3] >= 0.0 |
最適化を実行します。
1 2 3 4 | optimize!(model2) termination_status(model2) value(x[1]), value(x[2]), value(x[3]) objective_value(model2) |
1 2 3 | OPTIMAL::TerminationStatusCode = 1 (0.0, 2.5, 2.3) 9.8 |
以上、Julia(JuMP,GLPK)で線形計画法の問題を解く方法を紹介してきました。
変数、関数、条件を与えれば、すぐに解いてくれるので便利です。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Optim)で2変数関数の最小値・最大値を求める方法