線形分数変換とは：反転1/zを例に

どうも、木村（@kimu3_slime）です。

今回は、線形分数変換とは何か、反転\(\frac{1}{z}\)を例に紹介します。

\(f(z)= \frac{2z-1}{z-2}\)のように、線形関数の比として表される複素関数を、線形分数変換（一次分数変換、linear fractional transformation）と呼びます。メビウス変換（Möbius transformation）とも。

一般的な形は、\(f(z)=\frac{az+b}{cz+d}\)です。ただし、\(ad – bc \neq 0\)という条件をつけますが、それは分母が常に0になったり、定数関数となったりする退化したケースを除外するためです。

線形分数変換はシンプルな正則関数であり、その等角写像としての性質（全単射）を利用して、複雑な領域の問題を円盤など単純な領域に持ち込むために利用されます。

今回は、そんな線形分数変換を理解するために、反転\(\frac{1}{z}\)について考えましょう。

一般的な線形分数変換\(f(z)=\frac{az+b}{cz+d}\)は、\(+b \)や\(+d\)する平行移動、\(az\)や\(cz\)による拡大縮小・回転、\(1/z\)という反転の組み合わせ（合成）でできています。

平行移動と拡大縮小回転はシンプルですが、反転は少し複雑です。そこで何が起こっているか調べてみましょう。

極形式\(z=re^{i\theta}\)で表すと、反転は\(\frac{1}{z}= \frac{1}{r}e^{-i\theta}\)です。つまり、大きさが\(\frac{1}{r}\)になり、偏角は\(-\theta\)と実軸に対して反転されます。

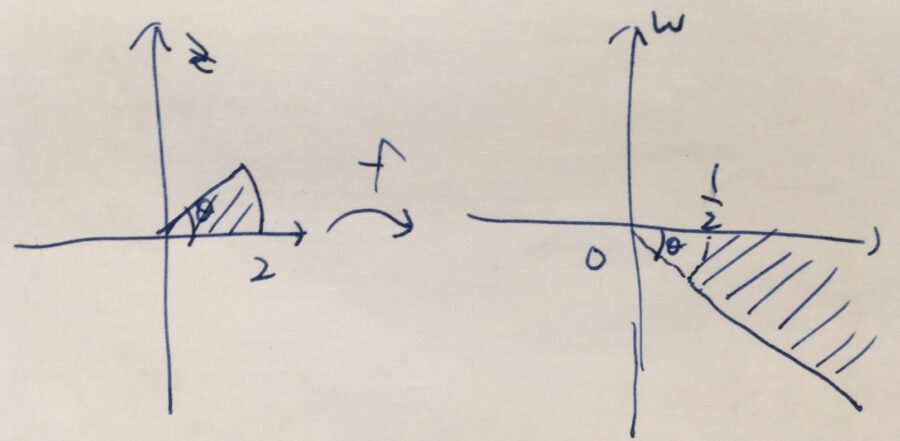
例えば、半径\(2\)の扇形は、半径\(\frac{1}{2}\)の扇形の外側へと写ります。\(z=\frac{1}{2}\)は\(f(z)=2\)へ写るように、原点に近い点は原点から遠くの点へと写ることに注意しましょう。つまり、大きさの面では単位円周\(|z|=1\)に関する反転となっています。

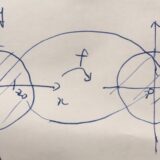
\(|z|=R\)という円周を考えれば、その像もまた\(|f(z)|= \frac{1}{R}\)という円周になります。つまり、円が円に写るような性質を持っていますね。特に、\(R=1\)の円（単位円盤）は単位円盤自身に写されます。

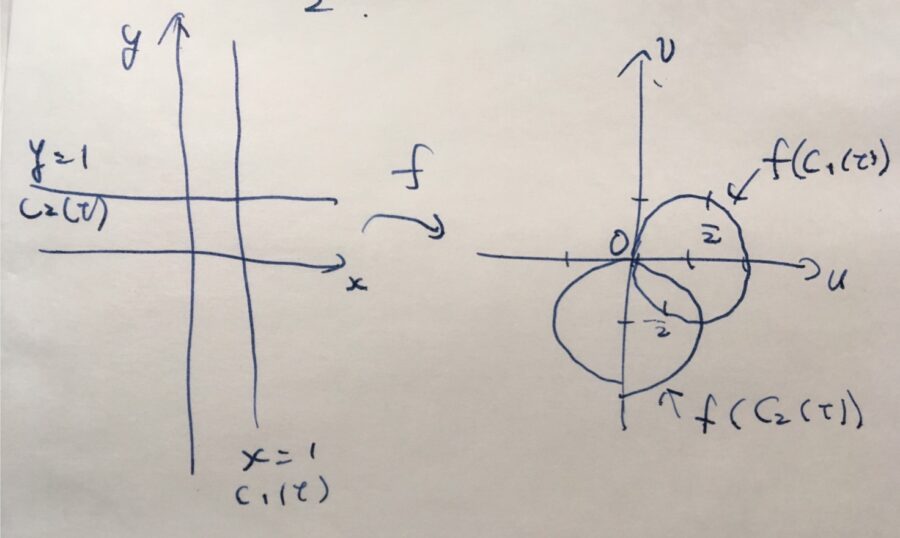
直交座標を使い、実部や虚部が一定の直線、\(x=1\)や\(y=1\)がどう写るか考えてみましょう。\(C_1(t)= 1+ti\)、\(C_2(t)=t+ i\)と直線を表すと、その像は\(\frac{1}{C_1(t)}=\frac{1}{1+ti}=\frac{1-ti}{1+t^2}\)といったようになります。この軌跡は、円です。なぜなら、

\[ \begin{aligned}|f(C_1(t))-\frac{1}{2}| \\ = |\frac{1-ti}{1+t^2} -\frac{1}{2}|\\=|\frac{-\frac{1}{2}t^2+\frac{1}{2} -ti}{1+t^2}|\\ =\sqrt{\frac{(-\frac{1}{2}t^2+\frac{1}{2})^2+t^2}{(1+t^2)^2}}\\ =\sqrt{\frac{\frac{1}{4}(t^4+2t^2 +1)}{(1+t^2)^2}} \\ =\frac{1}{2}\end{aligned} \]

となるので。同様に、\(|f(C_2(t)) +\frac{1}{2}i |=\frac{1}{2}\)です（確かめてみてください）。これらを図示すれば、次のようになります。直線が円に写っています。

また、特殊な直線として、\(x=0\)や\(y=0\)を考えましょう（ただし原点を除く）。その像は、\(\frac{1}{ti}=-\frac{1}{t}i\)、\(\frac{1}{t}\)となるように、\(v=0\)、\(u=0\)という直線に写っています。つまり、直線が直線に対応しています。

反転変換\(\frac{1}{z}\)によって、いくつかの円や直線が、円や直線に写されるのを見てきました。

この性質は一般化されます。つまり、すべての円や直線は、反転によって円や直線に写されます。

さらに、反転に限らず一般の線形分数変換でも同様で、円や直線は、線形分数変換によって円や直線に写されます。

証明については、例えば「Advanced Engineering Mathematics」を参照してください。

これらの対応関係は、しばしば円円対応と呼ばれています。無限遠点\(\infty\)を付け加えた複素平面（リーマン球面）を考えると、直線を無限遠点を通る円として捉えることができることが知られています。この立場から、直線も円の一種として見れば、線形分数変換は円を円に対応させる性質を持っている、と言えるわけです。

以上、線形分数変換とは何か、反転\(1/z\)を例に紹介してきました。

領域の変形において線形分数変換は便利ですが、その性質のひとつとして、円や直線がまた円や直線に写るという性質を見ました。

簡単な例を題材に、計算と図示の両方をしてみると、線形分数変換がどんな変換なのか、理解しやすくなるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。