どうも、木村(@kimu3_slime)です。
今回は、Julia(Plotly)でグリグリ動かせるインタラクティブな3Dグラフを作る方法を紹介します。
準備
PlotsとPlotlyJSを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("Plots") Pkg.add("PlotlyJS") |
グラフを描く準備として、以下のコードを実行します。
1 2 | using Plots plotlyjs() |
これによって、PlotsとPlotlyJSが動くようになります。
僕の環境だと「The WebIO Jupyter extension was not detected. See the WebIO Jupyter integration documentation for more information. 」というメッセージが出ますが、以降の実行には影響がありませんでした。
2変数関数の3Dグラフ
例として、いくつかの2変数関数の3Dグラフを描いてみましょう。
\[ \begin{aligned}f(x,y)=x^2+y^2\end{aligned} \]
1 2 3 | x = y = range(-5, 5, length=300) f(x, y) = x^2+y^2 surface(x, y, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
「range」は描写する範囲の指定です。\(x,y\)ともに-5から5まで、300分割して値を取ることにします。
「surface(x, y, f)」によって、3D曲面のグラフが描けます。他の文字列はオプションです。
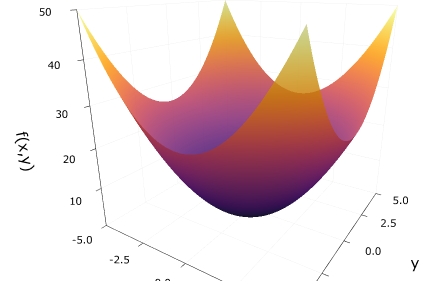
スクロールによって拡大縮小、ドラッグで回転ができます。
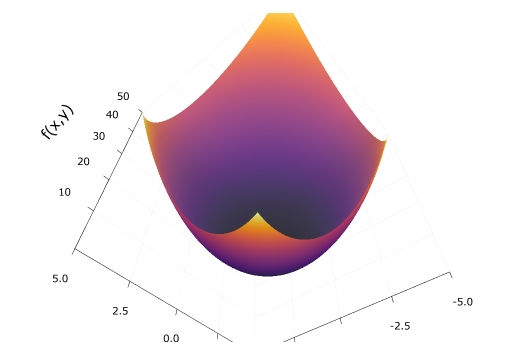
「wireframe」によって、網掛けのグラフが作れます。
1 | wireframe(x,y,f) |
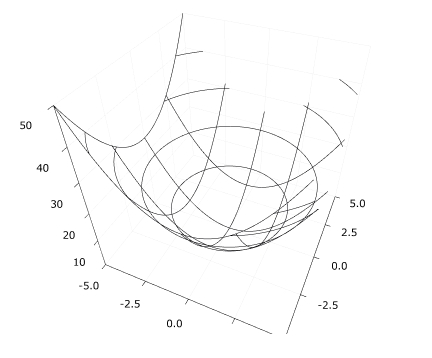
「contour」によって、等高線が描けます。
1 | contour(x,y,f) |
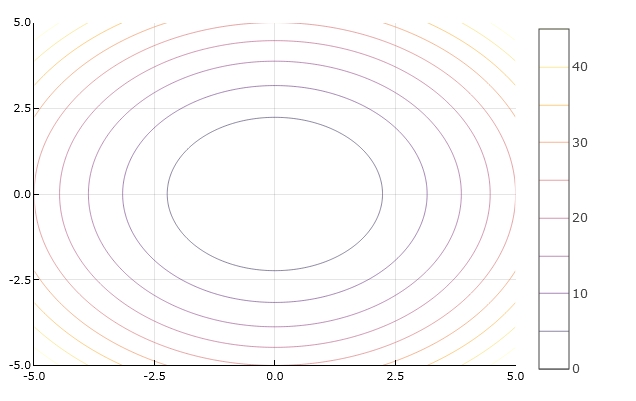
他の例も同様にして描くことができます。
\[ \begin{aligned}f(x,y)=x^2-y^2\end{aligned} \]
1 2 3 | x = y = range(-5, 5, length=300) f(x, y) = x^2-y^2 surface(x, y, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
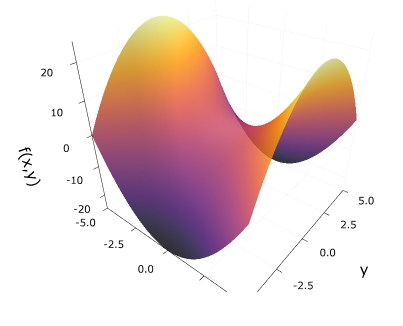
\[ \begin{aligned}f(x,y)=xy\end{aligned} \]
1 2 3 | x = y = range(-5, 5, length=300) f(x, y) = x*y surface(x, y, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
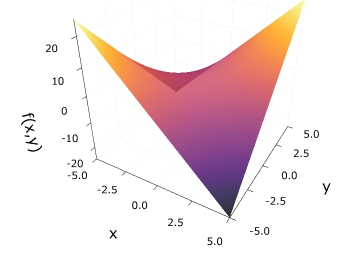
最後に、
\[ \begin{aligned}f(x,y)=x^2+y^2\end{aligned} \]
に\((1,1)\)における接平面
\[ \begin{aligned}g(x,y)=2(x-1)+2(y-1)+2\end{aligned} \]
を合わせたグラフを描いてみましょう。
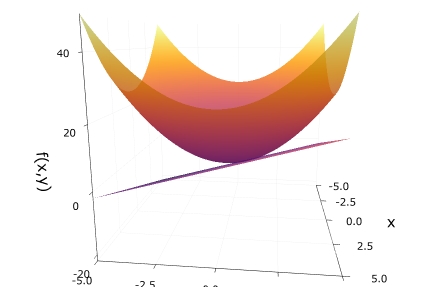
1 2 3 4 5 | x = y = range(-5, 5, length=300) f(x, y) = x^2+y^2 g(x,y)= 2(x-1)+2(y-1)+2 surface(x, y, f,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") surface!(x, y, g,colorbar=false, alpha=0.9 ,xlabel = "x", ylabel = "y", zlabel = "f(x,y)") |
「surface!」を使うことで、グラフを重ねて描くことができます。

回転させると、ちょうど接しているのがよくわかります。
以上、Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法を紹介してきました。
インタラクティブな3Dグラフを作るために、これまで僕はgnuplotを利用していました。
今回の方法ならば、Juliaでも同じくらいの簡単さで3Dグラフが作って触れます。2変数関数の理解には、3Dグラフを自分で触ってみるのが最初の一歩としてとても良いです。ぜひこの方法を試してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)