Juliaで数列の計算、棒グラフを描く方法

どうも、木村（@kimu3_slime）です。

今回は、Juliaで数列の計算、棒グラフを描く方法を簡単に紹介します。

Plotsのインストール
数列の計算、棒グラフ
こちらもおすすめ

Plotsのインストール

グラフ描写用のパッケージ、Plotsをインストールしておきましょう。既にインストールしてある場合、飛ばしてください。

using Pkg
Pkg.add("Plots")

1 2	using Pkg Pkg.add("Plots")

数列の計算、棒グラフ

準備として、Plotsを使えるようにしておきましょう。

using Plots

1	using Plots

描きたい数列を配列として定義し、それをplotを使って描くのが基本的なステップです。

等比数列\(a_n = 2n+1\)を描いてみましょう。

x=[2n+1 for n in 1:50]
plot(x,st=:bar, label="a_n")

1 2	x=[2n+1 for n in 1:50] plot(x,st=:bar, label="a_n")

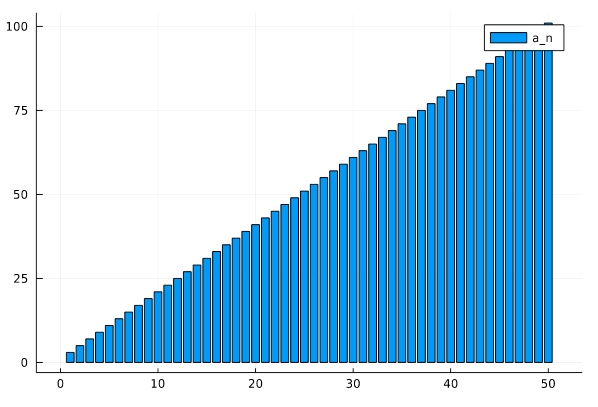
「x=[2n+1 for n in 1:50]」は、\(3,5,7,\dots\)といった数列を、配列として生成しています。変数は\(n\)で、その動き範囲が1から50までです。2n+1を変えることで数列の形を、1:50を変えることで描写する範囲を変えられます。

「plot(x,st=:bar, label=”a_n”)」で棒グラフの描写です。「bar(x, label=”a_n”) 」でも同様の結果が得られます。

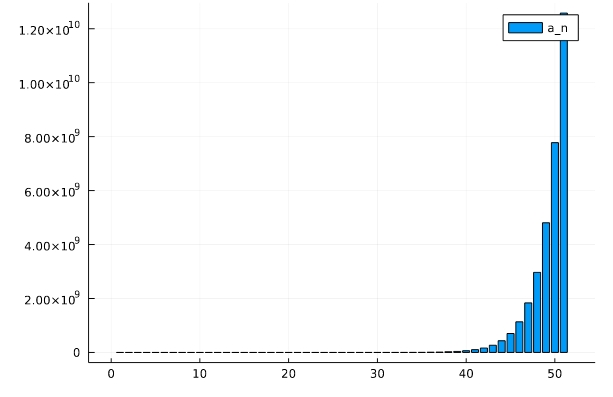
等比数列\(a_n =2 \cdot3^{n-1}\)も、同様にして描けます。ただし、桁が大きくなるとオーバーフローが起こってしまうので、BigIntを使ってきちんとした結果が出るようにしました。

x=[2*BigInt(3)^(n-1) for n in 1:50]
plot(x,st=:bar, label="a_n")

1 2	x=[2*BigInt(3)^(n-1) for n in 1:50] plot(x,st=:bar, label="a_n")

偶数、奇数項によって数列の定義が違うケースを考えてみましょう。

\[ \begin{aligned}b_n= \begin{cases}0 & (nが偶数 )\\ \frac{4}{n\pi} & (nが奇数)\end{cases}\end{aligned} \]

を描いてみます。

x=[(if n % 2 == 0 0 else 4/(n*pi) end) for n in 1:50]
plot(x,st=:bar, label="b_n")

1 2	x=[(if n % 2 == 0 0 else 4/(n*pi) end) for n in 1:50] plot(x,st=:bar, label="b_n")

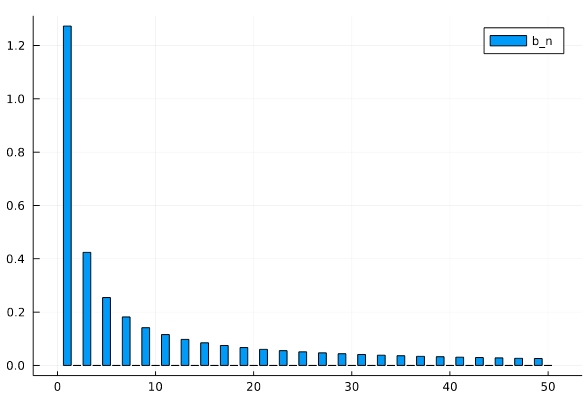
数列の定義式が「(if n % 2 == 0 0 else 4/(n*pi) end)」と変わりました。もし\(n\)を2で割ったあまりが0ならば（偶数ならば）0という値、そうでないならば（奇数ならば）\(\frac{4}{n\pi}\)という値、という意味です。

さらに条件分岐を増やした数列も、同様にして描くことができます。

\[ \begin{aligned}b_n= \begin{cases} \frac{8}{n^2 \pi} & (nを4で割ったあまりが1) \\ -\frac{8}{n^2 \pi} & (nを4で割ったあまりが3) \\ 0 & (nが偶数)\end{cases}\end{aligned} \]

を描いてみます。

x=[(if n % 4 == 1 8/(n^2 *pi) elseif n % 4 == 3 (-8/(n^2 *pi)) else 0 end) for n in 1:50]
plot(x,st=:bar, label="b_n")

1 2	x=[(if n % 4 == 1 8/(n^2 pi) elseif n % 4 == 3 (-8/(n^2 pi)) else 0 end) for n in 1:50] plot(x,st=:bar, label="b_n")

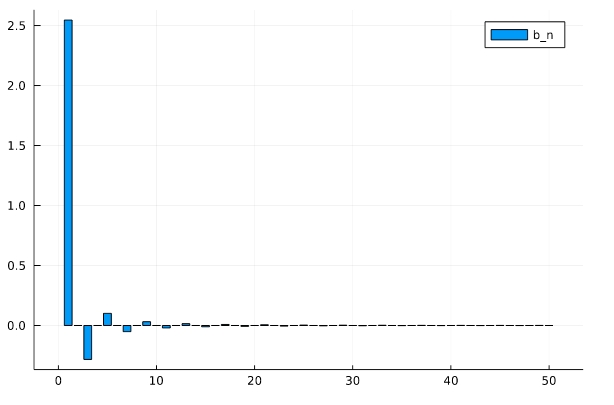
「elseif 条件式値」によって、条件が追加できます。「n % 4 == 3 (-8/(n^2 *pi))」と値にかっこをつけましたが、「n % 4 == 3 -8/(n^2 *pi)」と書くと期待する結果にならないので注意しましょう。「3 -8/(n^2 *pi)」がひとまとまりとして解釈されるようです。

例外的な初項が加わった数列を描いてみましょう。

\[ \begin{aligned}a_0 = \frac{2}{\pi}\end{aligned} \]

\[ \begin{aligned}a_n= \begin{cases}0 & (nが奇数)\\ -\frac{4}{(n^2-1) \pi } & (nが偶数)\end{cases}\end{aligned} \]

x=append!([2/pi],[(if n % 2 == 1 0 else -(4/(pi*(n^2-1))) end) for n in 1:50])
plot(x,st=:bar, label="a_n")

1 2	x=append!([2/pi],[(if n % 2 == 1 0 else -(4/(pi*(n^2-1))) end) for n in 1:50]) plot(x,st=:bar, label="a_n")

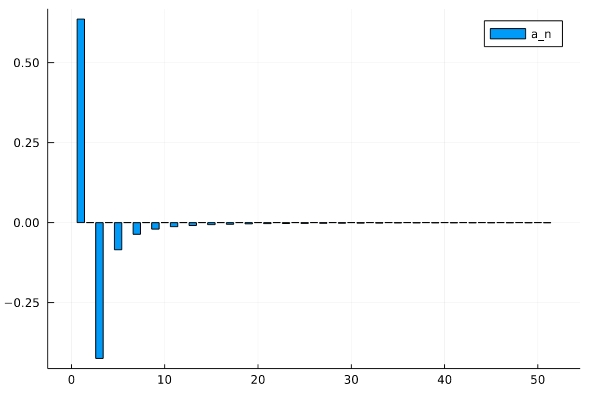
「append!(配列1,配列2)」によって、\(\frac{2}{\pi}\)を配列として最初に追加しています。「pushfirst!(配列, 値)」でも同様の結果が得られます。

最後に、フィボナッチ数列

\[ \begin{aligned} a_0=0,a_1=1 \\ a_{n+2}=a_n+a_{n+1} \end{aligned} \]

を描いてみましょう。

function Fib(n)
    a,b = 0,1
    for i in 1:n
        a,b = b, a+b
    end
    return a
end

@time x=[Fib(n) for n in 0:50]
plot(x,st=:bar, label="a_n")

function Fib(n)

a,b = 0,1

for i in 1:n

a,b = b, a+b

end

return a

end

@time x=[Fib(n) for n in 0:50]

plot(x,st=:bar, label="a_n")

51-element Array{Int64,1}:
           0
           1
           1
           2
           3
           5
           8
          13
          21
          34
          55
          89
         144
           ⋮
    63245986
   102334155
   165580141
   267914296
   433494437
   701408733
  1134903170
  1836311903
  2971215073
  4807526976
  7778742049
 12586269025

51-element Array{Int64,1}:

144

⋮

63245986

102334155

165580141

267914296

433494437

701408733

1134903170

1836311903

2971215073

4807526976

7778742049

12586269025

if文で素朴に書く（Fib(n)= Fib(n-2)+Fib(n-1)）と実行が遅かったです。そこで、for文で書けるように工夫をしました。「a,b = b, a+b」が漸化式の計算です。(0,1)から始めて、(1,0+1),(1,1+1),(2,2+1),(3,3+2)という計算をn回繰り返します。

以上、Juliaで数列の計算、棒グラフを描く方法を紹介してきました。

Plotsを使い、数列を配列として定義し、それをプロットします。難しいのは、配列としての定義の仕方だと思います。ぜひ試行錯誤してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。