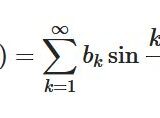偶関数・奇関数のフーリエ級数、係数の求め方、証明

どうも、木村（@kimu3_slime）です。

今回は、偶関数・奇関数のフーリエ級数、係数の求め方、証明を紹介します。

偶関数・奇関数のフーリエ級数、係数の求め方
証明
こちらもおすすめ

偶関数・奇関数のフーリエ級数、係数の求め方

まず、偶関数と奇関数の定義を確認しておきましょう。偶関数とは、\(f(-x)=f(x)\)を満たす関数です。\(\cos x\)や\(x^2\)などがそうですね。奇関数とは、\(f(-x)=-f(x)\)を満たす関数です。\(\sin x\)や\(x^3\)などが例です。

偶関数や奇関数のフーリエ級数、係数は、次のようにシンプルに求めることができます。\(f\)を周期\(2L\)の関数としましょう。

\(f\)が偶関数のときは、

\[ \begin{aligned}f(x)= a_0 +\sum_{k=1}^\infty a_n \cos \frac{n\pi x}{L}\end{aligned} \]

\[ \begin{aligned}a_0 =\frac{1}{L}\int_0^L f(x)dx\end{aligned} \]

\[ \begin{aligned}a_n = \frac{2}{L}\int_0^L f(x) \cos \frac{n\pi x}{L} dx \end{aligned} \]

となります。コサインのみの級数となり、フーリエコサイン級数と呼ばれるものです。

\(f\)が奇関数のときは、

\[ \begin{aligned}f(x)=\sum_{n=1}^\infty b_k \sin \frac{n\pi x}{L}\end{aligned} \]

\[ \begin{aligned}b_n = \frac{2}{L}\int_0^L f(x) \sin \frac{n\pi x}{L} dx \end{aligned} \]

となります。サインのみの級数となり、フーリエサイン級数と呼ばれるものです。

参考：フーリエサイン・コサイン級数とディリクレ・ノイマン境界条件の関係

証明

一般に、周期\(2L\)の関数\(f\)のフーリエ級数展開、係数は

\[ \begin{aligned}f(x)=a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi x}{L} +b_n \frac{n\pi x}{L})\end{aligned} \]

\[ \begin{aligned}a_0=\frac{1}{2L} \int_{-L}^{L} f(x)dx\end{aligned} \]

\[ \begin{aligned}a_n=\frac{1}{L} \int_{-L}^{L} f(x)\cos \frac{n\pi x}{L}dx\end{aligned} \]

\[ \begin{aligned}b_n=\frac{1}{L} \int_{-L}^{L}f(x) \sin \frac{n\pi x}{L} dx\end{aligned} \]

となります（フーリエ係数に関するオイラーの公式）。

また、一般論として、偶関数、奇関数の積分は次のように簡略化できます。

\(g\)が偶関数ならば、

\[ \begin{aligned}\int_{-L}^{L}g(x) dx \\ = \int_{-L}^0 g(x)dx +\int_{0}^L g(x)dx \\ =\int_{0}^{L}g(-y)dy+\int_{0}^L g(x)dx \\=\int_{0}^{L}g(y)dy+\int_{0}^L g(x)dx \\= 2\int_{0}^L g(x)dx \end{aligned} \]

です（変数変換、積分範囲の入れ替えと符号に注意）。\(g\)が奇関数ならば、

\[ \begin{aligned}\int_{-L}^{L}g(x) dx \\ = \int_{-L}^0 g(x)dx +\int_{0}^L g(x)dx \\ =\int_{0}^{L}g(-y)dy+\int_{0}^L g(x)dx \\=-\int_{0}^{L}g(y)dy+\int_{0}^L g(x)dx \\= 0 \end{aligned} \]

です。偶関数なら半分の区間で2倍、奇関数ならば0です。

また、偶関数同士の積、奇関数同士の積は偶関数です。偶関数と奇関数の積は奇関数です。順に確かめてみます。

\[ \begin{aligned}f(-x)g(-x)= f(x)g(x)\end{aligned} \]

\[ \begin{aligned}f(-x)g(-x) = -f(-x)(-g(x))= f(x)g(x)\end{aligned} \]

\[ \begin{aligned}f(-x)g(-x)= f(x)(-g(x)) = -f(x)g(x)\end{aligned} \]

これらの性質を利用して、フーリエ係数を計算していきましょう。

まず、\(f\)が偶関数のときを考えます。積の性質から、\(f \cos\)は偶関数、\(f \sin\)は奇関数です。したがって、

\[ \begin{aligned}a_0=\frac{1}{2L} \int_{-L}^{L} f(x)dx\\ =\frac{1}{L} \int_{0}^{L} f(x)dx\end{aligned} \]

\[ \begin{aligned}a_n=\frac{1}{L} \int_{-L}^{L} f(x)\cos \frac{n\pi x}{L}dx \\ =\frac{2}{L} \int_{0}^{L} f(x)\cos \frac{n\pi x}{L}dx\end{aligned} \]

\[ \begin{aligned}b_n=\frac{1}{L} \int_{-L}^{L}f(x) \sin \frac{n\pi x}{L} dx\\ =0\end{aligned} \]

となります。

続いて、\(f\)が奇関数のときを考えます。積の性質から、\(f \cos\)は奇関数、\(f \sin\)は偶関数です。したがって、