三角・指数・対数関数と多項式の不等式：テイラー展開に関連して

どうも、木村（@kimu3_slime）です。

今回は、テイラー展開に関連して得られる、三角・指数・対数関数と多項式の不等式を紹介します。

三角・指数・対数関数の不等式

紹介するのは、多項式との比較をする不等式です。

\(x \geq 0\)のとき、

\[ \begin{aligned} x – \frac{x^3}{6} \leq \sin x \leq x\end{aligned} \]

\[ \begin{aligned} 1- \frac{x^2}{2} \leq \cos x \leq 1- \frac{x^2}{2}+\frac{x^4}{24}\end{aligned} \]

\[ \begin{aligned} 1+x+\frac{x^2}{2} \leq e^x \end{aligned} \]

\[ \begin{aligned}x- \frac{x^2}{2} \leq \log(1+x) \leq x- \frac{x^2}{2}+\frac{x^3}{3}\end{aligned} \]

が成り立ちます。

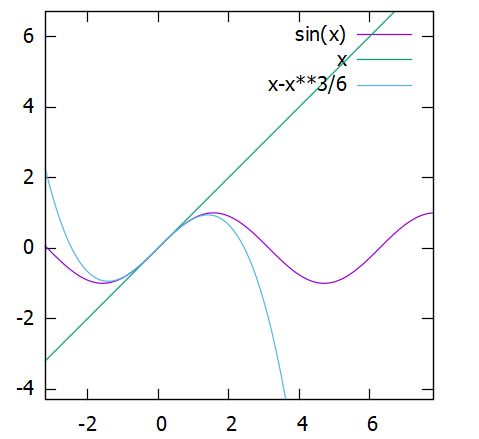
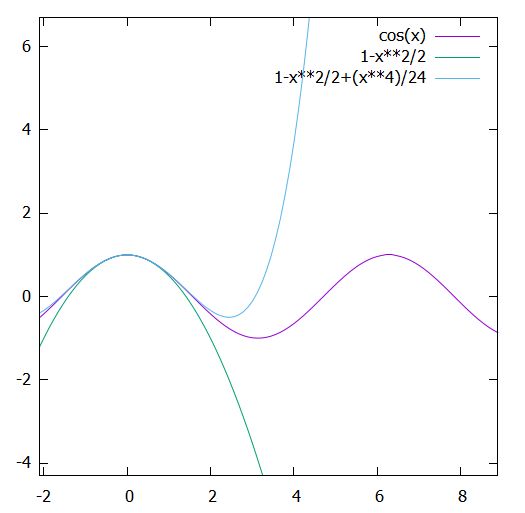
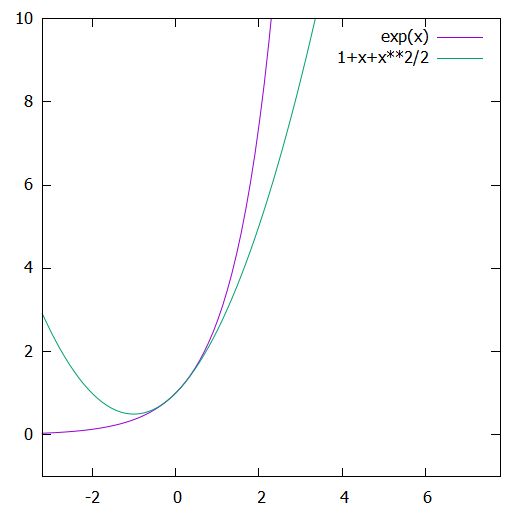
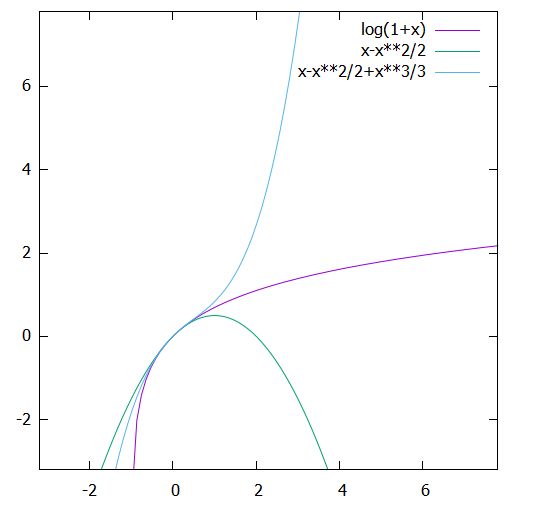
これらの不等式は、単に差を取って微分し、単調性を確かめて示すことができます。

より大きな背景としては、テイラー展開（マクローリン展開）に関連するものであると知っておくと良いでしょう。

テイラーの定理によると、\(x \geq 0\)に応じて、

\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots\\ + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_{n+1}(x)\end{aligned} \]

\[ \begin{aligned}R_{n+1}(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\end{aligned} \]

\[ \begin{aligned}\sin x = x-\frac{\sin c}{6}x^3\end{aligned} \]

\[ \begin{aligned}\sin x = (\sin c)x\end{aligned} \]

\[ \begin{aligned}\cos x = 1-\frac{\cos c}{2}x^2 \end{aligned} \]

\[ \begin{aligned}\cos x = 1-\frac{x^2}{2}+ \frac{\cos c}{4!} x^4\end{aligned} \]

\[ \begin{aligned}e^x = 1+x+\frac{e^c}{2}x^2 \end{aligned} \]

\[ \begin{aligned}\log (1+x) = x-\frac{x^2}{2}+ \frac{\frac{2}{(1+c)^3}}{3!} x^3\end{aligned} \]

\[ \begin{aligned}\log (1+x) = x-\frac{x^2}{2}+ \frac{x^3}{3}- \frac{\frac{3!}{(1+c)^4}}{4!} x^4\end{aligned} \]

を満たす\(0< c<x\)が存在します。\(c\)は関数によって別物ですが、記述の簡略化のため同じ記号で書きました。

これを使って、不等式を導いていきましょう。\(x \geq 0\)なので、すべて\(x^n \geq 0\)であることに注意します。

\(-1 \leq \sin c \leq 1\)より

\[ \begin{aligned} \sin x &= x-\frac{\sin c }{6}x^3 \\ & \geq x-\frac{x^3}{6} \end{aligned} \]

\[ \begin{aligned} \sin x &= (\sin c) x \\ &\leq &x \end{aligned} \]

です。\(-1 \leq \cos c \leq 1\)より、

\[ \begin{aligned} \cos x &= 1-\frac{\cos c}{2}x^2 \\ & \geq1-\frac{x^2}{2} \end{aligned} \]

\[ \begin{aligned} \cos x &= 1-\frac{x^2}{2}+ \frac{\cos c}{4!} x^4 \\ &\leq 1-\frac{x^2}{2}+\frac{x^4}{24} \end{aligned} \]

です。\(e^c \geq e^0 \geq 1\)より

\[ \begin{aligned} e^x &= 1+x+\frac{e^c}{2}x^2\\ & \geq1+x+\frac{x^2}{2} \end{aligned} \]

です。\(c>0\)より、\(\frac{1}{(1+c)^3}>0\)、\(-\frac{1}{(1+c)^4} <0\)なので、

\[ \begin{aligned} \log x &= x-\frac{x^2}{2}+ \frac{\frac{2}{(1+c)^3}}{3!} x^3 \\ & \geq x-\frac{x^2}{2} \end{aligned} \]

\[ \begin{aligned} \log x &= x-\frac{x^2}{2}+ \frac{x^3}{3}- \frac{\frac{3!}{(1+c)^4}}{4!} x^4\\ &\leq x-\frac{x^2}{2}+\frac{x^3}{3} \end{aligned} \]

が得られました。

三角関数と対数関数は、展開したときに正負の項が交互に登場するため、挟み込む不等式を作り出すことができました。しかし、指数関数は下から評価する式しか作れませんでした。

\(x\)を大きくしていくとき、指数関数は無限大に発散するどんな多項式よりも速く発散します。それが上から評価できない理由です。同じように、対数関数は無限大に発散するどんな多項式よりも遅く発散します。それでも今回、対数関数を下から評価できたのは、（正の）無限大に発散する多項式とは比較していないからです。

参考：多項式・指数・対数関数の極限、増大のスピード比較

以上、三角・指数・対数関数と多項式に関する不等式、テイラー展開との関係を紹介してきました。

高校数学や大学入試でこのような不等式はよく見かけますが、その背景としてテイラー展開を知っておくと理屈に納得しやすいでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。