多項式・指数・対数関数の極限、増大のスピード比較

どうも、木村（@kimu3_slime）です。

多項式、指数、対数関数は、\(x\)を大きくすると無限大に発散しますが、そのスピードには違いがあります。今回は、指数関数的な増大の強さ、無限大での極限の発散のスピードを比較した結果を紹介します。

発散のスピード

今回比較したい関数は、\(\log_e x, x^a ,x^b , e^x\)です。ただし、\(0<a<b\)とします。どの関数も、\(x\)が大きくなれば限りなく大きくなり、\(x\to \infty\)で無限大に発散するという点は同じです。

しかし、その発散のスピードが違います。結論から言えば、対数関数が最も遅く、多項式（べき関数）はその中間で、指数関数が最も速いです。

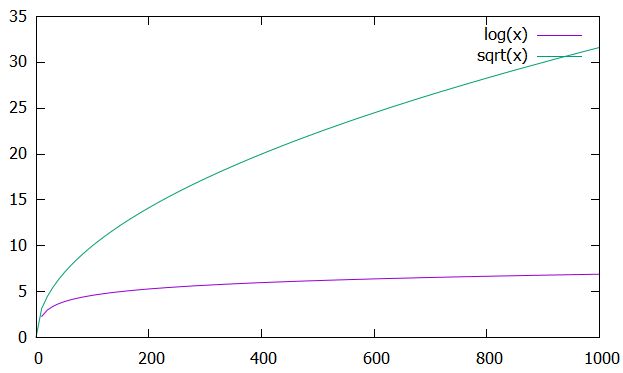
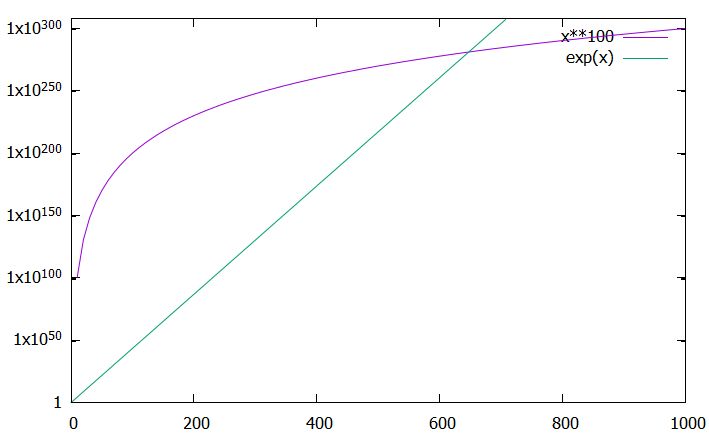
指数関数の図では、縦軸が対数目盛となっている、つまり\(\log x^{100},\log e^x\)のグラフであることに注意。巨大な数は対数スケールでないと変化が目で追えません。

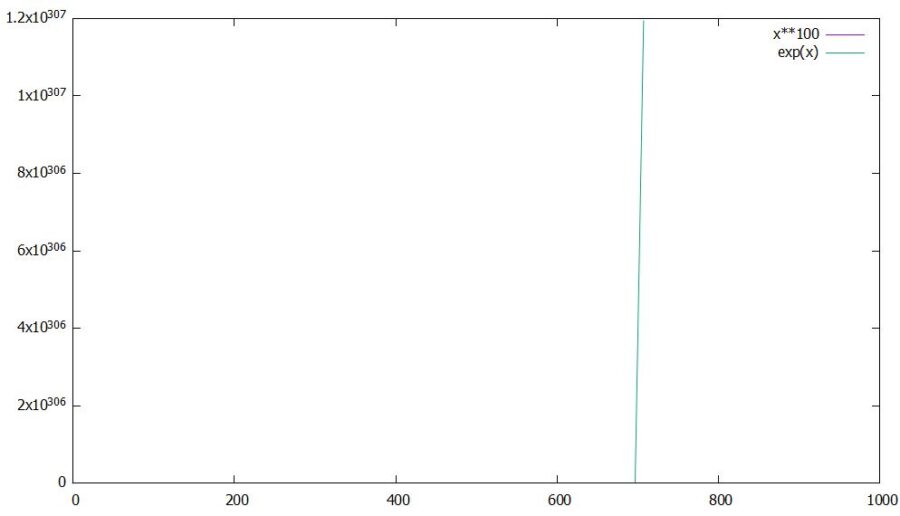
この発散のスピードは、極限の言葉を使えば次のように表せるものです。

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^a}{\log_e x}= \infty\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^b}{x^a}= \infty\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{e^x}{x^b}= \infty\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{\log_e x}{x^a}= 0\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^a}{x^b}= 0\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^b}{e^x}= 0\end{aligned} \]

\(\log_e x\)より\(x^a\)の方が「より速く」無限大に近づくというイメージは、この極限によって表されています。分母分子ともに無限大へ向かうという点は同じですが、比を取って比べると、どちらが勝っているかわかります。\(x^a\)より\(x^b\)、\(x^b\)より\(e^x\)の方がより速く増大するわけです。

ここでは多項式というよりは、単純に\(x^a\)のようなべき関数を考えています。多項式も、無限大に発散するようなものならば、結局は最高次数の大きさによって発散のスピードが変わるので。

以上の結果はなぜそうなるのか、証明してみましょう。

まず基本的な事実として、\(x>0\)のときこれらの関数を微分すると

\[ \begin{aligned}(\log_e x)^\prime = \frac{1}{x}\end{aligned} \]

\[ \begin{aligned}(x^a)^\prime = a x ^{a-1}\end{aligned} \]

\[ \begin{aligned}(e^x)^\prime = e^x\end{aligned} \]

となります。対数関数はその値が大きくなるほど、変化率\(\frac{1}{x}\)が小さくなるので、めちゃくちゃ遅く増大していそうです。一方、指数関数は変化率が\(e^x\)そのものなので、\(e^x\)が大きくなるほど変化率がさらに増えて爆発的に増加しそうです。べき関数は、次数が1落ちるので、中間くらいですね。

まず、べき関数はべきの指数が大きいほど速く発散することについて。これは単純にひとまとめにして、

\[ \begin{aligned} \lim_{x\to \infty} \frac{x^a}{x^b}&= \lim_{x\to \infty} \frac{1}{x^{b-a}} \\&=0 \end{aligned} \]

ですね。\(b-a>0\)なので、\(\lim _{x \to \infty}x^{b-a}= \infty\)となるからです。

続いて、べき関数\(x^b\)と指数関数\(e^x\)の比較について。

\(b\)は一般に実数であり自然数ではありませんが、\(b\)より大きな自然数\(n\)を使って比べます。例えば、\(x>0\)において

\[ \begin{aligned}\frac{1}{n!} x^n \leq e^x\end{aligned} \]

という不等式が成り立つことが示せます。

これはテイラー展開

\[ \begin{aligned}e^x = \sum_{k=0}^\infty \frac{1}{k!}x^k\end{aligned} \]

を知っていると簡単です（そもそも、この式を指数関数の定義とすることがある）。\(x>0\)のとき右辺は正の数の和の極限であり、有限個\(n\)までの和の方が当然少なくなるので。

知らなくても、繰り返し微分をすれば不等式を導くことができます。

\[ \begin{aligned}f_n (x) = e^x – \sum_{k=0}^n \frac{1}{k!}x^k\end{aligned} \]

と置き、\(x \geq 0\)、\(n\)が自然数のとき、\(f_n (x) \geq 0\)を示せば良いです。

数学的帰納法で示します。\(n=1\)のとき、\(f_1 ^\prime (x) =e^x -1\)なので、\(x\geq 0\)では単調増加です。さらに\(f_1(0)=e^0-1=0\)なので、\(f_1(x) \geq 0\)と言えました。

\(n=\ell\)、\(\ell\)は自然数のとき、\(f_\ell (x) \geq 0\)と仮定しましょう。このとき、

\[ \begin{aligned} (f_{\ell+1})^\prime (x) &= e^x -\sum_{k=0}^\ell \frac{1}{k!}x^k \\&= f_{\ell}(x) \\ & \geq 0 \end{aligned} \]

で、\(x \geq 0\)のとき\(f_{\ell +1}\)は単調増加です。また、\(f_{\ell+1}(0)=e^0-1=0\)なので、\(f_{\ell+1}(x) \geq 0\)が言えました。

よって、\(x>0\)のとき

\[ \begin{aligned} 0 &<&\frac{ x^b}{e^x} \\ & \leq \frac{ x^n }{e^x}\\ &= \frac{x^{n+1} }{ xe^x } \\ & \leq \frac{(n+1)! e^x}{x e^x}\\ &= \frac{(n+1)! }{x} \end{aligned} \]

で、\(n\)は\(x\)に依存していないことに注意すれば、\(\lim_{x\to \infty}\frac{(n+1)!}{x} =0\)。はさみうちの原理から

\[ \begin{aligned}\lim _{x\to \infty} \frac{x^b}{e^x}=0\end{aligned} \]

が示せました。

最後に、対数関数\(\log _e x\)とべき関数\(x^a\)の比較をします。

\(y= \log _e x\)と置くと、\(x \to \infty\)のとき\(y \to \infty\)でもあります。また、べき関数の定義から、\(x^a =e^{a \log_e x}=e^{ay}\)です。\(z=ay\)と置けば、\(a>0\)から\(x\to \infty\)のとき\(z\to \infty\)でもあります。よって、べき関数と指数関数の結果を使うことができ、

\[ \begin{aligned} \lim_{x\to \infty} \frac{x^a}{\log_e x} &= \lim_{y \to \infty} \frac{y}{e^{ay}} \\ &= \lim_ {z\to \infty}\frac{\frac{1}{a}z }{e^z}\\&= 0\end{aligned} \]

と言えました。

収束のスピードを比較する結果

\[ \begin{aligned}\lim_{x\to \infty} \frac{\log_e x}{x^a}= 0\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^a}{x^b}= 0\end{aligned} \]

\[ \begin{aligned}\lim_{x\to \infty} \frac{x^b}{e^x}= 0\end{aligned} \]

は、ランダウの記号を使えば、

\[ \begin{aligned}\log_e x = o(x^a)\quad(x\to \infty)\end{aligned} \]

\[ \begin{aligned}x^a = o(x^b)\quad(x\to \infty)\end{aligned} \]

\[ \begin{aligned}x^b = o(e^x)\quad(x\to \infty)\end{aligned} \]

と表せます。対数関数はどんなべき関数よりも高次の無限小、べき関数同士はべきが小さい方が高次の無限小、どんなべき関数も指数関数より高次の無限小です。

発散のスピードの速さは、関数のオーダーとも呼ばれます。複雑な関数であっても、結局\(x\to \infty\)において、対数・べき関数・指数のどのオーダーで増大するのか判別するのは大事です。

コンピュータサイエンス・アルゴリズムの分野では、インプット数\(n\)に対する計算時間\(f(n)\)がどのオーダーなのか考えます。多項式時間で解ける問題はP問題、どうやっても多項式時間にならない問題はNP問題と呼ばれるものです。