部分空間の共通部分、和空間とは：例と証明

どうも、木村（@kimu3_slime）です。

今回は、線形代数学における部分空間の共通部分、和空間とは何か、具体例と証明を紹介します。

部分空間の共通部分
部分空間の和空間
こちらもおすすめ

部分空間の共通部分

線形空間\(\mathbb{R}^3\)における例を考えましょう。

\(W_1 :=\{x \in \mathbb{R}^3 \mid x_1+x_2+x_3=0\}\)、\(W_2 :=\{x \in \mathbb{R}^3 \mid x_2+x_3=0\}\)と置きます。\(W_1 ,W_2\)はそれぞれ1次方程式により定まる集合で、\(\mathbb{R}^3\)の部分空間となります。幾何学的には、2つの平面です。

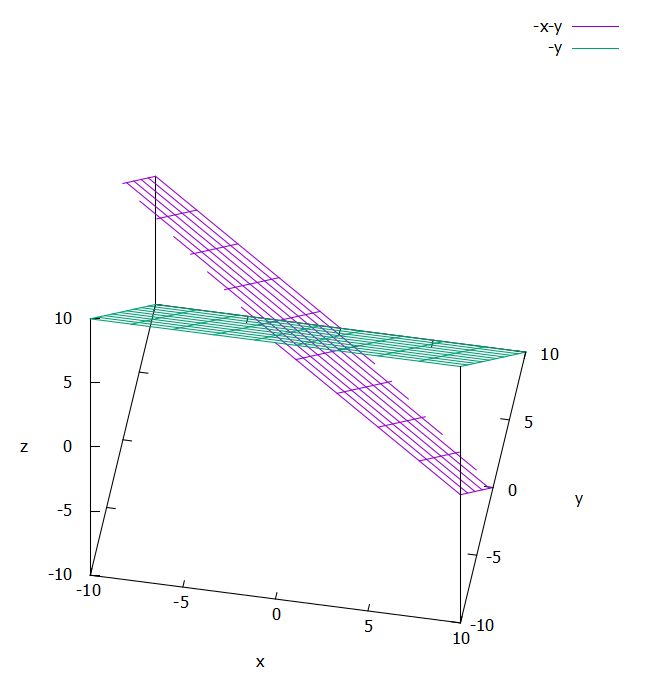
さて、これらの共通部分、交わりについて考えましょう。\(W_1 \cap W_2 =\{x \mid x_1+x_2 +x_3=0 かつ x_2+x_3 =0\}\)です。\(x_1 =0\)という平面上における直線になっていますね。

これが部分空間になっていることを確かめてみましょう。部分空間とは、和とスカラー倍について閉じた部分集合のことでした。

\(x,y \in W_1 \cap W_2\)を任意に選びます。和を考えると、\((x_1+y_1)+(x_2+y_2)+(x_3+y_3)\\ = (x_1+x_2+x_3)+(y_1+y_2 +y_3 )=0\)で、\((x_2+y_2)+(x_3+y_3)\\= (x_2+x_3)+(y_2+_y3)=0\)。よって、\(x+ y \in W_1 \cap W_2\)です。また、\(x \in W_1 \cap W_2\)、\(a \in \mathbb{R}\)とすると、\(ax_1+ax_2 +ax_3 =a(x_1+x_2+x_3)=0\)、\(ax_2+ax_3 = a(x_2+x_3)=0\)。よって、\(ax \in W_1 \cap W_2\)であることがわかりました。

2つの部分空間の共通部分を考えると、それは部分空間になっていました。これは偶然ではなく、一般化される性質です。

\(V\)を線形空間、\(W_1, W_2\)をその部分空間とします。このとき、\(W_1 \cap W_2\)も\(V\)の部分空間となります。

確かめてみましょう。\(x,y \in W_1 \cap W_2 \)、\(a \in \mathbb{R}\)とします。\(W_1\)は部分空間なので、\(x+y ,ax \in W_1\)です。\(W_2\)も部分空間なので、\(x+y , ax \in W_2\)です。よって、\(x+y, ax \in W_1 \cap W_2\)が言えました。

部分空間の共通部分は、必ず部分空間となります。それは交空間と呼ばれることがあるようです。

部分空間の和空間

では、共通部分の次には和集合を考えてみましょう。

\(W_1 , W_2\)が部分空間のとき、\(W_1 \cup W_2\)も部分空間となるのでしょうか？　……共通部分と事情が違い、必ずしもなりません。

ごく簡単な例として、\(\mathbb{R}^3\)の部分空間として、\(W_1 =\{x \mid x_1 =0\}\) ,\(W_2 =\{x \mid x_2 =0\}\)について考えてみましょう。

その和集合は、\(W_1 \cup W_2 = \{ x \mid x_1 =0 または x_2=0\}\)です。単に2つの平面を足し合わせた集合。

これは部分空間になっていません。例えば、\(x= (0,1,0)\)、\(y=(1,0,0)\)とすると、\(x, y \in W_1 \cup W_ 2\)です。しかし、その和は\( x+y = (1,1,0) \not \in W_1 \cup W_2\)となるので。

部分空間の和集合を考えるだけでは、その全体が部分空間としての役割を果たすこと（和、スカラーについて閉じていること）は保証されません。今回のような例では、単独には線形空間として機能していますが、全体としてはバラバラです。

つまり、\(W_1 \cup W_2\)は、部分空間になるには要素が不足しているのです。では、それらを含んでいるような部分空間を考えることはできないでしょうか。

そこで、2つの部分空間の線形和を

\[ \begin{aligned}W_1 + W_2 := \{z \mid x \in W_1 ,y \in W_2 によって z= x+y と表せる\}\end{aligned} \]

と定めましょう。集合について使われている\(+\)は、新しい記号で、その意味は右辺によって定まっています。

これは、\(W_1 ,W_2\)の要素の線形結合によって表される要素の集合、\(W_1 \cup W_2\)が生成する集合です。

上に挙げた\(W_1, W_2\)の例で、\(W_1 + W_2\)が部分空間となっていることを確かめましょう。例えば、さきほど扱ったベクトルの和は\( x+y = (1,1,0) \in W_1 + W_2\)と含まれるようになっています。

実際は、\(W_1 + W_2 = \mathbb{R}^3\)という関係が成り立ちます。右辺は部分空間なので、これを確かめれば十分です。

\(W_1,W_2\)は部分空間なので、その要素の和は必ず\(\mathbb{R}^3\)のベクトルとなり、\(W_1 +W_2 \subset \mathbb{R}^3\)となることは良いでしょう。逆に、\(z \in \mathbb{R}^3\)とします。\(z= (0,z_2,z_3)+(z_1,0,0)\)と分解できます。\(x=(0,z_2,z_3)\)、\(y= (z_1,0,0)\)と見れば、線形和の定義から\(z \in W_1 + W_2\)がわかりました。

具体例に限らず、一般にこの性質は成り立ちます。

つまり、\(V\)を線形空間、\(W_1 ,W_2\)をその部分空間とするとき、線形和\(W_1+W_2\)は部分空間です。

確かめましょう。任意に\(z ,w \in W_1+ W_2\)を選ぶと、\(z =p+q, w =r+s\)、\(p,r \in W_1\)、\(q,s \in W_2\)と表されます。和は\(z+w= (p+r)+(q+s)\)と表されます。\(W_1,W_2\)は部分空間なので、\(p+r \in W_1\)、\(q+s \in W_2\)。線形和の定義から、\(z+w \in W_1 +W_2\)です。また、スカラー倍についても、\(W_1,W_2\)は部分空間なので、\(ap \in W_1\)、\(aq \in W_2\)。したがって、\(az = a(p+q)=ap+aq\)なので、線形和の定義から\(az \in W_1 +W_2\)が言えました。

そこで、\(W_1 +W_2\)を和空間と呼びます。

和空間は、\(W_1 ,W_2\)を含む最小の部分空間であることが知られています。

最小であるとはどういうことかというと、\(W\)を\(W_1,W_2\)を含む任意の部分空間とするとき、\(W_1 +W_2 \subset W\)が常に成り立つということです。どんな部分空間を考えても、和空間はそれより包含関係について小さくなる。

確かめてみましょう。\(W\)を\(W_1,W_2\)を含む部分空間とします。\(W_1+W_2 \subset W\)を示せば良いです。\(z \in W_1+ W_2\)とすると、\(z=x+y\)、\(x \in W_1, y \in W_2\)と表されます。\(W_1 \subset W, W_2 \subset W\)より、\(x,y \in W\)です。\(W\)は部分空間なので、\(z= x+y \in W\)です。よって、\(W_1+W_2 \subset W\)が言えました。

部分空間の和集合\(W_1 \cup W_2\)は必ずしも部分空間になりません。そこで要素を付け足して部分空間を考えるわけですが、なんでも付け足して全体\(V\)を常に考えることになってしまったら意味がありません。\(W_1 +W_2\)は、線形空間であるために過不足ない要素の加え方をしている、と言えますね。

以上、部分空間の共通部分、和空間とはどういうものか、例や証明を紹介してきました。

共通部分は素直に部分空間になりますが、和集合は必ずしもそうではありません。そこで単なる集合和ではなく、線形和という特殊な和を考えると、和空間になりました。共通部分と和空間の次元、直和の考え方については、別記事で紹介予定です。

一般論として共通部分や和空間について考えるのは、最初のうちは難しいでしょう。まずはこの記事で紹介したような、2,3次元レベルの例を作って、共通部分や和集合・和空間がどんな形をしているのかイメージし、部分空間かどうか判定してみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。