どうも、木村(@kimu3_slime)です。
中学から高校の数学では、傾き、変化の割合、平均変化率、微分係数といった言葉を学びます。似たものではあるのですが、今回はその違いをやさしく解説していきます。
傾きと変化の割合、平均変化率
今回紹介する用語は、どれも関数に関するものです。
簡単な関数の例として、グラフが直線の形をした関数、1次関数(線形関数)があります。
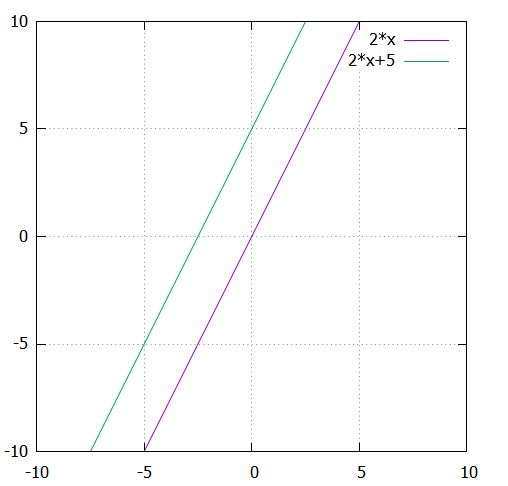
上のグラフは、\(y=2x\)と\(y=2x+5\)のグラフです。縦方向にずれていますが、傾きは同じです。
このように傾きは、直線を坂と見たときの傾きの険しさ(急さ)を表しています。一般的には、1次関数\(y= ax +b\)の\(a\)を傾き(slope)・勾配(gradient)と呼びます。\(x\)が1増えると、\(y\)は\(a\)だけ値を増しているわけです。
\(b\)は直線を平行移動させるもので、\(b\)が異なる2つの1次関数のグラフがあっても、\(a\)が同じなら平行な2つの直線ができあがります。
傾きの考え方は、基本的に1次関数・直線に対して使われるものです。
1次関数以外の関数を考えるときには、変化の割合(rate of change)、ないし平均変化率(average rate of change)という言葉を使います。中学では変化の割合、高校では平均変化率と呼ぶようですが、どちらも同じ意味です。
例えば、止まっている状態から走り出す車の運動を考えましょう。\(x\)を出発してから経った時間として、移動距離を\(y\)とすると、\(y=x^2\)といった関係が成り立ちます。
\(y=x^2\)のような2次関数を考えると、そこには一定の傾きというものが存在しません。それでも、車の移動速度を考えたいとします。例えば、\(x=0\)から\(x=5\)までの間に位置はどれだけ変化するでしょうか。それは
\[ \begin{aligned}\frac{yの変化量}{xの変化量}= \frac{5^2 -0^2}{5-0}=5\end{aligned} \]
と表されます。
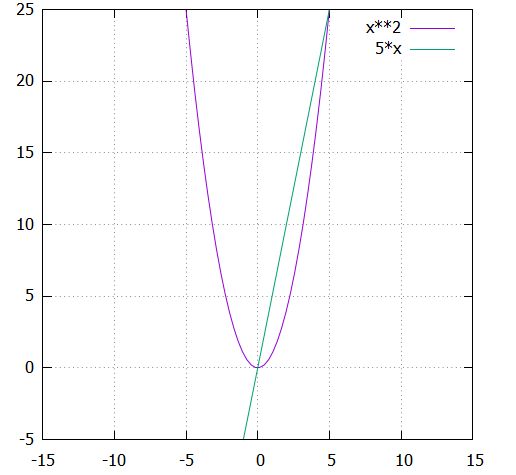
この\(x\)の変化量に対する関数\(y\)の変化量の割合を、変化の割合、または平均変化率と呼びます。グラフで言えば、グラフ上の2点\((0,0)\)、\((5,25)\)をつなぐ直線の傾きを求めることに対応しています。
\(x\)が0から5まで変化するときの、といった「どの区間で変化を見ているか」という前置きが重要です。例えば、\(x\)が0から1まで変化するときの\(y\)の変化の割合は、
\[ \begin{aligned}\frac{1^2 -0}{1-0}=1\end{aligned} \]
となり、\(x\)が0から5まで変化するときの変化率と違っています。\(y=x^2\)という2次関数では、変化の割合・平均変化率は、注目する区間によって一般に異なるのです。
一般に、関数\(y= f(x)\)が\(x=c\)から\(x=d\)まで変化するときの変化の割合、平均変化率は、
\[ \begin{aligned}\frac{yの変化量}{xの変化量}= \frac{f(d)-f(c)}{d-c}\end{aligned} \]
と定義されます。分子\(f(d)-f(c)\)が\(y\)の変化量であり、分母\(d-c\)によって割ることで、平均した変化量を求めているわけです。
傾きと、変化の割合・平均変化率の考え方は、一般には別物です。
ただし、1次関数の変化の割合・平均変化率を求めると、それは必ず傾きに一致します。
\(y= ax+b\)が、\(x=c\)から\(x=d\)まで変化するときの変化の割合・平均変化率は、
\[ \begin{aligned}\frac{(ad+b)-(ac+b)}{d-c}= \frac{a(d-c)}{d-c}=a\end{aligned} \]
となるので。どんな変化の区間\(c,d\)を見ても、常に変化率が一定になっている。1次関数とは、変化の割合が一定である関数とも言うことができます。
微分係数とは
平均変化率は、関数を時間\(x\)における位置を\(f(x)\)と表すものと見たときに、平均の速度に対応したものでした。
例えば、5分で250m移動したら、平均の速度は\(250/5 =50\)(m/分)であると考えるのが、平均変化率の考え方です。
しかし、加速している車の運動ならば、詳しく見れば速さは時々によって変化しているはずです。最初はゆっくりで、だんだんと速くなっていきます。車の速度メーターを見たことがあるなら、それが時々で変化しているのが見て取れるでしょう。このような瞬間の速さを捉えるにはどうしたら良いでしょうか。
瞬間の変化率(instantaneous rate of change)というものを考えるには、平均変化率で考える区間をどんどん小さくしていけば良いのではないでしょうか。
\(y=x^2\)として、\(x=1\)における瞬間の変化率を求めたいとしましょう。\(x=1\)から\(2\)までの変化率、\(1\)から\(1.1\)、\(1\)から\(1.01\)までの変化率は、
\[ \begin{aligned}\frac{4-1}{2-1}=3\end{aligned} \]
\[ \begin{aligned}\frac{1.1^2 -1}{1.1- 1}=2.1\end{aligned} \]
\[ \begin{aligned}\frac{1.01 ^2 -1}{1.01-1}= 2.01\end{aligned} \]
となっています。

考える区間の幅を小さくすると、どんどんその割合は\(2\)に近づいていきそうです。区間の幅を文字\(h\)で表すと、\(1\)から\(1+h\)まで変化するときの変化率は
\[ \begin{aligned}\frac{(1+h)^2-1^2}{(1+h)-1}=\frac{h^2 +2h}{h}= h+2\end{aligned} \]
であり、その値は\(h\)を\(0\)にどんどん近づけていくと、2に近づいていきます。この値を近づける操作を、
\[ \begin{aligned}\lim _{h \to 0}\frac{(1+h)^2-1^2}{(1+h)-1} = 2\end{aligned} \]
と表します(\(\lim\) は極限と呼ばれるもの。高校数学で学ぶ)。
このように区間の大きさを小さくしていったときに、平均変化率が近づく値のことを、(関数\(y=x^2\)の\(x=1\)における)微分係数(differential coefficient)と呼び、\(f^{\prime }(1)= 2\)と書きます。微分係数とは、瞬間の変化率のことであり、関数を運動として見るならば瞬間の速度のことです。
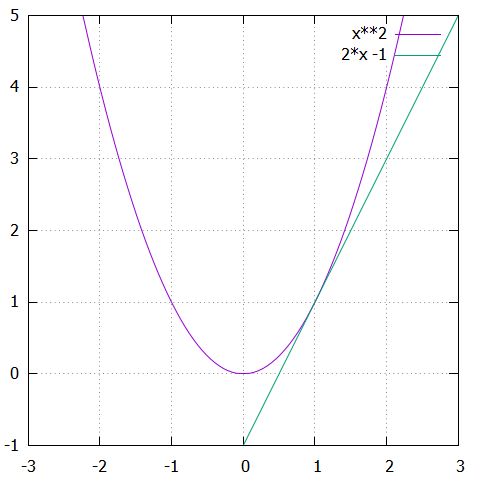
微分係数\(2\)を傾きとした直線\(y=2x-1\)を考えると、それは\(y=x^2\)の\(x=1\)においてグラフに接する直線:接線(tangent line)となっています。
平均変化率を使った直線は、曲がったグラフそのものに一般に一致することはありません。しかし、瞬間の変化率:微分係数を使った直線は、注目する点の付近ではかなりグラフに近い=接した状態になっています。
一般に、関数\(y=f(x)\)の\(x=a\)における微分係数は
\[ \begin{aligned}f^{\prime }(a):=\lim _{h \to 0} \frac{f(a+h)-f(a)}{(a+h)-a}\end{aligned} \]
として定義されます。
さまざまな点\(x\)における微分係数を計算していくと、\(f(x)=x^2\)に対して、\(f^{\prime}(x)=2x\)であることがわかります。この関数を、\(f\)の導関数(derivative)と呼び、導関数を求めることを\(f\)を微分する(differentiate)と言います。
\(f(x)=x^2\)を加速する運動の位置を表す関数として見るとき、その微分、導関数\(f^{\prime}(x)=2x\)は、(瞬間の)速度を表しています。したがって、\(x=1\)ならば傾きが\(2\)の直線で表されるペースで変化していますが、だんだん加速して\(x=5\)ならば傾き\(10\)の直線で表されるペースで変化していることがわかりました。
以上、傾き、変化の割合・平均変化率、微分係数の違いを紹介してきました。
- 傾き:直線の傾き具合の大きさ。\(y=ax+b\)における\(a\)。
- 変化の割合=平均変化率:\(x\)が一定の区間で変化するときの、関数の変化の割合。
- 微分係数:瞬間の変化率。平均変化率で考える区間の大きさを、限りなく小さくしていったときに近づく値。
傾きは直線、一次関数に対して定義される単純な概念です。
そして、変化の割合:平均変化率は、一次関数以外のより広い関数の変化率を捉えようとする考え方です。
平均変化率は曲がった関数をラフに直線近似する考え方ですが、微分係数:瞬間の変化率はそれを虫眼鏡のように細かく近似できます。
これらの概念を段階を踏んで理解すれば、微分の考え方を直観的に捉えられるようになるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。