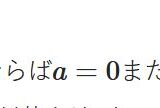相関関係と因果関係の例、疑似相関に注意しよう

どうも、木村（@kimu3_slime）です。

僕が大学生のときに、「相関と因果は必ずしも一致しないって、有名な話だよね」と友人に話をしたとき、それが通じなくて驚いた記憶がありました。

人々の考えやニュースにおいては因果関係はよく主張されますが、少なくないものが誤りを含んでいます。

今回は、相関関係と因果関係とは何かを例を通じて紹介し、見せかけの相関-疑似相関に気をつけよう、という話をしていきましょう。

相関関係と因果関係の例
疑似相関に注意しよう
こちらもおすすめ

相関関係と因果関係の例

相関や因果「関係」という言葉は、主に2つの量にどんな対応関係があるか、を問うものです。

人口が増えるほど、お店の数は増えるか
8月に蒸し暑い日が多い地域ほど、エアコンの設置率は増えるか
お米を食べる家ほど、パンを食べないか
出生率が高い地域ほど、死亡率は下がっているか

こうした2つの量の間の関係を調べるときは、それをデータとして記録し、平面に並べた散布図（scatter plot）がよく使われます。

引用：統計学入門

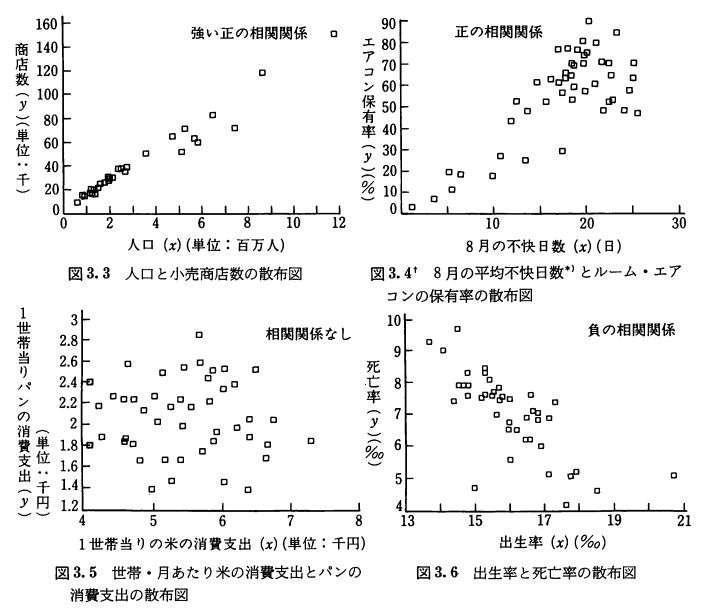
上の図のデータによれば、

人口が増えるほど、お店の数は増えるか
8月に蒸し暑い日が多い地域ほど、エアコンの設置率は増えるか
出生率が高い地域ほど、死亡率は下がっているか

という3つは、一方の量\(x\)が増えたり減ったりするのにしたがって、もう一方の量\(y\)が増えたり減ったりする、という対応関係があります。この対応関係があるとき、2つのデータ\(x,y\)は相関関係（correlationship）にあると呼ばれます。

一方、パンとコメの消費は、特に互いに関係がなさそうです。コメを食べるからといってパンを食べなくなるわけでもないし、パンを食べるからといってコメを食べなくなるわけでもない。こうした場合は、相関関係がない、と呼びます。

散布図から得られる印象でなく、よりフォーマルに論じるには、例えば相関係数と呼ばれる式を用います。ピアソンの積率相関係数と呼ばれるものを使えば、データ\(x,y\)が直線的な関係にあるかどうかが、計算によって\(-1\)以上\(1\)以下の数\(r\)として求められます。

特に、\(r\)が1に近い、すなわち\(x\)の増加で\(y\)が増加するときは正の相関関係にある。\(r\)が\(-1\)に近い、すなわち\(x\)の増加で\(y\)が減少するときは負の相関関係にあると呼ばれます。\(r\)が0に近いときは、相関関係はないと見られるわけです。

ピアソンの積率相関係数はよく使われるため、単に相関係数、相関関係というときに、それを指しているケースが多いです。ただしその測り方には限界があって、直線的な関係があるかどうかしか測れないわけです。そりゃ全くバラバラなケースに相関はないですが、曲線的な相関関係も考えられます。相関関係は、狭義には線形な関係があるかを指す言葉ですが、広い意味では\(y\)が\(x\)の関数として表せるような規則性が見られるかどうかを指しています。

因果関係（causation）は、一方が原因、もう一方が結果の関係にあるかどうかを意味します。

人口の増加が原因で、お店の数が増える
8月に蒸し暑さが引き金となって、エアコンの設置する施設が増える
お米を食べることが原因で、パンを食べなくなる
出生率が高いことが原因で、死亡率が下がる

前者の2つは、およそ因果関係があるのではないか、と見られます。

もしかしたら1つ目は、お店が増えるから人口が増加する、という逆の因果関係もあるかもしれません。一方で、エアコンを設置する施設が増えるからといって、決して蒸し暑日が増減するわけではありませんね。このケースでは逆の因果関係はありません。

お米とパンのケースは、そもそも量的な関係、相関関係がないので、因果関係もないと考えられるでしょう。

出生率と死亡率の関係では、相関関係はありますが、因果関係があるとは思えません。その地域の病院の数という第3の変数を調べるとどうなるでしょうか。病院の数が多いから、出生率が増えて死亡率が減る。両者の増減の要因が、別にあったというパターンです。

因果関係は、基本的に判断が難しいものです。相関係数のように計算によって判断することができず、個々の分野の知識や事実との整合性も使って考えることになります。

疑似相関に注意しよう

この記事で伝えたいことは、相関関係があるからといって、因果関係があるとは結論できないということです。

統計の本ではしばしば書かれていますが、この考え方は未だに人々にきちんと知られておらず、強調してもしすぎることはないと思っています。

たとえば、次のような議論はよく見られるものです。

子どものゲーム時間と成績の関係をデータを取って調べた。ゲーム時間が増えるほど、成績が悪いという結果が得られた。だから、ゲームの時間を制限すべきだ。

データによって、ゲーム時間と成績の間に、負の相関が見られたとしましょう。そこに相関関係はあることは確かです。だからといって、そこに因果関係があるとは限らないのです。すなわち、ゲーム時間を減らすことが、成績の増加につながるとは結論できないのです。

相関関係があって因果関係もあるように見えるが、それが見せかけの関係である（実際には因果関係にないと思われる）とき、疑似相関（spurious relationship）であると呼ばれます。

Spurious correlationsというサイトでは、多くの奇妙な相関関係（疑似相関）のデータを見ることができます。

画像引用：Spurious correlations

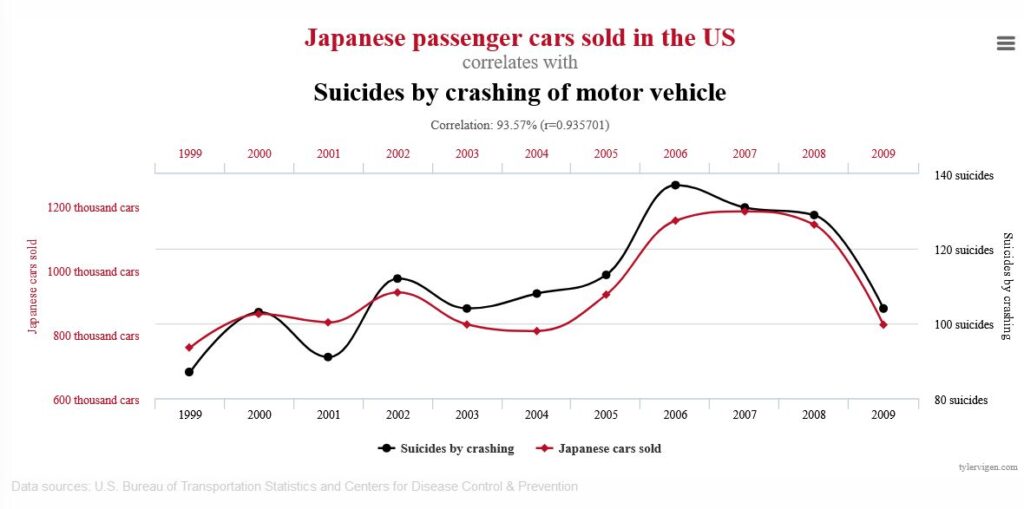
上の図は、アメリカでの乗用車の販売額と、車を使った自殺の数の関係を表したものです。例えばこれを悪意を持って「使え」ば、「最近、自動車自殺が増えている。それは日本車の販売者数とこんなに一致している。だから日本車の販売をやめるべきだ」といった結論に誘導できるかもしれません。

相関は因果を必ずしも意味しないと知っていれば、その議論の変な点には気づくことができるでしょう。そもそも、車の所有者数という第3の因子があって、車を使う人が増えたから、販売者数も自殺者数も増えた。日本車と自殺を結びつけた映画が流行ったなどの特殊なエピソードがない限りは、その2つに因果関係があるとは考えにくいだろう、といったように反論できますね。

以上、相関関係と因果関係の例、それらを区別し、「擬似相関ではないか？」と気をつける習慣をつけるとよい、という話をしてきました。

2つの量が似た傾向で変化しているからといって、そこに因果関係があるとは限らない。冷静になって考えれば納得できる人も多いのでしょうが、普段は意識していないと間違えやすいです。

しばしば、「因果関係がある」と考えたほうが、物事を単純に捉えられて、めんどくさくないんですよね（笑）。しかし真実を尊重したいならば、2つのデータに見られる「傾向」と「因果」を分離して捉えるようにする。それっぽい説や印象論、データがあっても、すぐに因果を結論しないように気をつけてみると良いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。