どうも、木村(@kimu3_slime)です。
中学校の数学では、関数というものを学ぶでしょう。
今回は、なぜ関数を学ぶのか、数理モデルという考え方を紹介します。
モデルを作って予測しよう
日本語でモデルというと、ポーズを取る仕事、モデルさんをイメージする人が多いかもしれません。また、プラモデルといえば、プラスチックでできた模型のことで、表したいものをマネしたモノを指した言葉です。
数学や科学におけるモデルは、説明したい現象を数式で表したもののことです。数理モデル、数学的モデル(mathematical model)とも。型・雛形を作ったり、法則性を見出す、シミュレーションをする、と言い換えても良いでしょう。
モデルの例として、アサガオの成長を考えてみましょう。観察日誌として、つるの長さを記録して、次のデータがあったとします。(架空のデータです)
| 実際のデータ | |
| 日数 | 長さ |
| 3 | 5 |
| 6 | 11 |
| 9 | 16 |
| 12 | 20 |
このデータから、アサガオのつるの成長のモデルを作ってみましょう。
日数と長さの関係を調べると、日数が2倍になると、長さもおよそ2倍になるように見えます。
この関係は、数学では関数を使って表すことができます。経過した日数を\(x\)、そのときのつるの長さを\(y\)とすると、
\[ \begin{aligned}y =\frac{5}{3} x\end{aligned} \]
という関数を考えるのが良さそうです。これをアサガオの成長モデルと呼ぶことにしましょう。
この関数は、1次関数、線形関数と呼ばれるものです。特に\(x,y\)は比例の関係にある、と呼ばれます。直線的な関係を想定するモデルなので、線形モデルとも。
このモデルにもとづいて計算をすると、次のようなデータが得られます。
| モデルによる予測 | |
| 日数 | 長さ |
| 3 | 5 |
| 6 | 10 |
| 9 | 15 |
| 12 | 20 |
\(6,9\)日目では、実際のデータとのずれ(誤差)が生じています。とはいえ、全体の傾向としては十分な予測ができていると言えるでしょう。
線形モデルは、単純なので予測によく使われています。次のグラフは、日本における年数と平均気温の関係を測ったデータに、直線的なモデルをあてはめたものです。
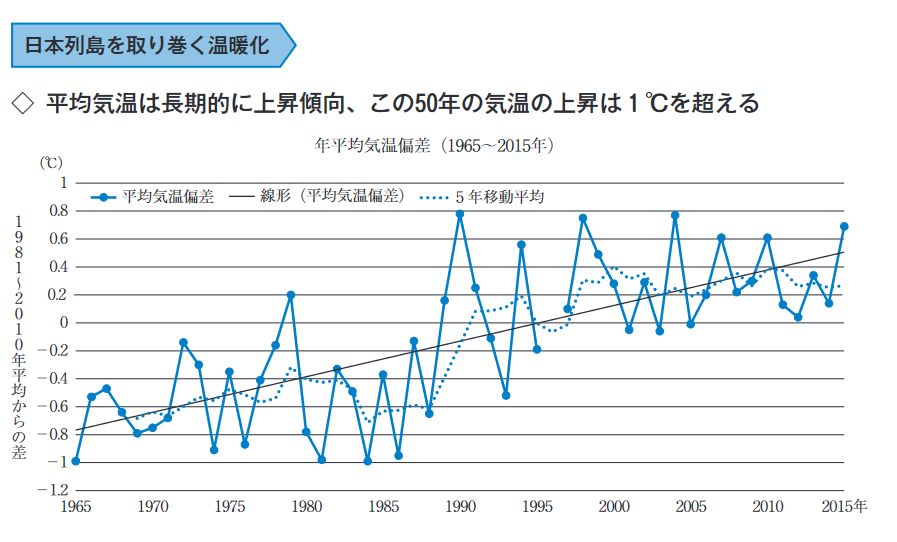
このように、直線的な変化を仮定することで、平均気温が上昇傾向にあることが読み取れますね。もしこのペースが変わらないならば、2065年にはさらに1℃上昇すると予想されます。
モデル、関数を考えるメリット
モデルを考えると、どんな良いことがあるでしょうか?
まずひとつに、持っていないデータの隙間を埋める、すなわち補間をすることができます。今回は、3の倍数の日にしか計測をしていません。しかしこのモデルを使えば、7日目の長さ\(y = \frac{5}{3} \cdot 7= 11+\frac{2}{3}\)であると推測されます。数少ないバラバラのデータ(離散データ)から、細かい精度での予測ができるようになりました。\(x\)はきっちりと整数でなくてもよく、\(6.5\)日目の長さを考えることもできます。
もうひとつは、未来の予測ができるということです。このペースでアサガオが成長するなら、\(x=30\)のときには\(y=50\)まで伸びていると予測されます。今回はアサガオでしたが、コメや野菜の成長ペースや収穫量をモデル化すれば、収穫までの期間や量を予測することもできるでしょう。
モデルと現実
数学というと、きっちりとした予測をしなければならないものではないか、と考える人がいるかもしれません。つまり、\(y =\frac{5}{3}\)は完全には当てはまっていないので、この関係は比例・一次関数とは言えない、と。
確かに厳密には当てはまってはいませんが、モデルと現実・測定データが完全に一致することはそもそもほぼありえません。そもそも、測定には一定の誤差が必ず含まれます。あくまで、モデルは現実や現象の模造品、近似に過ぎないわけです。その観点で言えば、このモデルはかなり誤差が少なく、良くできていると言えます。
統計学では、少ないデータから適切な連続的なモデル(関数)を作る方法は、回帰分析と呼ばれています。回帰分析においては、\(x\)は説明変数(独立変数)、\(y\)は目的変数(従属変数)と呼ばれるものです。「調べたい量を\(y\)として、それを\(x\)の変化によって説明できないか?」と考えるのは、科学において基本的な考え方になります。
線形モデルでは、データとの誤差を少なくするような傾きを決める必要がありますが、その方法として最小二乗法と呼ばれる方法が知られています。
詳しくは説明しませんが、\(y =\frac{5}{3} x\)ではなく、\(y =\frac{5}{3} x+\frac{1}{2}\)のモデルが、誤差の二乗和が\(1\)で最小となるモデルになっていて、その意味では「良い」モデルと言えるわけです。
参考:最小二乗法とは:最小二乗解の求め方、正規方程式、射影による理解
今回は、一次関数\(y=ax\)を使った線形モデルを考えましたが、すべての現象がこのような単純な直線関係で説明できるわけではありません。
例えば、車の教習では、車は急に止まれないことを学びます。具体的に言えば、走っている車が止まるまでにかかる距離は、速度の2乗に比例すると言われています。つまり、\(y= ax^2\)のような2次関数を考える必要が出てくるのです。
中学や高校の数学の時間では、1次関数や2次関数といった多項式関数、三角関数、指数関数、対数関数といったものを学ぶでしょう。いろいろな関数を学べば、より幅広い現象を精度良く説明できるモデルを考えられるようになるわけです。例えば、バネや振り子といった振動現象は、1次関数や2次関数で表現するよりも、三角関数を使うほうが適切です。モデリングを絵を描くことに例えるならば、関数は絵の具の色や絵画道具に対応します。
参考:サイン、コサインは何の役に立つ? バネの振動と三角関数
以上、中学校の数学でなぜ関数を学ぶか、数理モデルの考え方を紹介してきました。
「どうしてそんな関数が登場するか」を説明するには、微分方程式によるモデルや、統計モデル・確率モデルといった少し高度な数学が必要になるでしょう。
現実に起こっている現象を数値化・データ化して、それを関数・モデルを使って説明する。その考え方は、数学や科学の基本となるものです。ぜひ、数学の時間を通して、関数的・モデル的な考え方を養ってみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
PHP研究所 (2015-03-12T00:00:00.000Z)
¥855