微分方程式の解でなぜ指数関数（exp・ネイピア数）が現れるか

どうも、木村（@kimu3_slime）です。

常微分方程式の解には、指数関数（exp）がよく登場します。なぜ\(e\)（ネイピア数、オイラー数）を底とした指数関数を使うのでしょうか。その理由を簡単に紹介します。

微分方程式の解で指数関数（exp）を使う理由

ごく簡単な常微分方程式として、

\[ \begin{aligned}\frac{du}{dt} (t) = u(t)\end{aligned} \]

を考えましょう。

これは人口や生物の個体数\(u(t)\)が爆発的に状況を表す、マルサスモデルと呼ばれるものです。

参考：人類は必ず食糧問題に直面する？マルサスの法則と微分方程式

数学的には、微分してそれ自身になるような関数を見つける問題、と言えます。

オイラー数・ネイピア数\(e\)を使った指数関数\(u(t)= e^t \)は、そのような関数の例です。\(e\)が単なる文字でなく定数であることを強調するために、指数 exponential の頭文字を取って、\(\exp (t) := e^t\)と書くこともあります。

\(u(t)= e^t \)を微分すると、\(\frac{d }{dt }e^t= e^t \)となる、という性質があります（高校数学の微分、数学3）。つまり、\(u(t)= e^t \)は微分方程式の解（のひとつ）です。初期値を\(u(0)=u_0\)とするときの解は、\(u(t)= u_0 e^t\)となります。

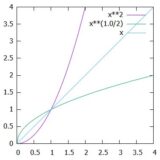
なぜ\(e^t\)を使わなければならないのでしょうか。例えば、\(2^t\)や\(10^t\)の方が、手でグラフを描くならば簡単そうです。

しかし、一般の指数関数\(a^t\)は、微分しても完全に元の形に戻ってくるわけではなく、

\[ \begin{aligned}\frac{d}{dt} a^t =( \log_e a) a^t\end{aligned} \]

となるのです。したがって、

\[ \begin{aligned}\frac{du}{dt} = (\log _e 2 )u\end{aligned} \]

\[ \begin{aligned}\frac{du}{dt} = (\log _e 10) u\end{aligned} \]

という微分方程式を、\(2^t\)、\(10^t\)はそれぞれ満たしています。微分方程式の形としては、\(\frac{du}{dt}= u\)よりも係数のずれがあって、シンプルではありませんね。

そもそも、微積分学や微分方程式における標準的な指数関数として、\(2^x\)や\(10^x\)でなく、\(e^x\)を考えるのは、\(\frac{d}{dx}e^x =e^x\)というシンプルな法則を満たすから、と言えます。

そういう性質を満たすような定数\(e\)があるので、それを使うと議論が簡単になるわけですね。

参考：なぜe（オイラー数）を学ぶ？指数関数、対数関数の微分を単純化

仮に微分方程式が

\[ \begin{aligned}\frac{du}{dt} (t) = ku(t)\end{aligned} \]

という形だとしても、解は指数関数で\(u(t) = u_0 e^{kt}\)と表せます。\(k>0\)、\(k<0\)によって、爆発増加するか減衰していくか、状況が分かれるのをイメージしてみてください。

さきほど考えた形、例えば \(k=\log _e 2 \)ならば、

\[ \begin{aligned} u(t) &= u_0 e^{(\log_e 2)t} \\ &=u_0 e^{(\log_e 2^t)} \\ &= u_0 2^t \end{aligned} \]

となります。途中で\(a^x = e^{(\log_e a ^x)}=e^{(\log_e a )x} \)という式変形を使っていますが、これが一般の指数関数\(a^x\)の定義（指数関数と対数関数は逆関数であること）です。

この例を見ればわかるように、結局は\(e^t\)という標準的な指数関数を使って微分方程式が解ければ（実際解きやすい）、\(2^t ,10^t\)といった一般的な指数関数が登場するケースにも対応できるわけです。だから、まずは\(e^t =\exp (t)\)を使って解ける微分方程式を学ぶことになるのでしょう。

以上、微分方程式の解において、なぜ指数関数（exp・ネイピア数）が現れるかを紹介してきました。

「微分する」という立場から見ると最も単純なのが\(e^t\)であり、それは単純であるだけでなく一般の指数関数をも含むものなのです。

\(e\)という定数は最初は慣れないかもしれませんが、微分方程式の学習を通して便利さを体感してみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。