どうも、木村(@kimu3_slime)です。
高校の数学では、不定積分と定積分というものを学ぶかと思います。不定積分は積分の公式のようなもので、面積を求める定積分において不定積分の式を活用する、という使い方をよく見るでしょう。
不定積分と定積分を学ぶ理由は、微分方程式というものと結びつけると明快になります。今回は、微分と積分の知識を前提に、簡単な微分方程式と不定積分・定積分との関係を紹介していきます。
参考:「運動」をイメージすればわかる、微分と積分入門、積分とは何か? 面積を長方形で近似計算してみよう
微分方程式とは
そもそも、高校数学の微積分を学ぶメリットのひとつが、微分方程式を理解できるようになることです。
微分方程式の例としてよく知られているのが、高校物理でも扱うニュートンの運動方程式です。
今回は、ボールが落ちていくような運動、自由落下(落体運動)を考えましょう。中学や高校の物理でよく題材となります。その運動方程式は、物体の質量を\(m\)、加速度を\(a\)、重力加速度(という定数)を\(g\)として、
\[ \begin{aligned}ma =- mg\end{aligned} \]
と表されます。加速度とは何か。物体の位置\(x\)を時間\(t\)の関数\(x(t)\)として表すとき、その微分が速度\(\frac{dx}{dt} =v(t)\)で、さらにそれを微分したものが加速度\(\frac{d^2 x}{dt^2} =a(t)\)です。さきほどの式の両辺を\(m\)で割ると、
\[ \begin{aligned} \frac{d^2 x}{dt^2} =- g\end{aligned} \]
という、関数\(x(t)\)の2回微分を含んだ方程式が得られます。「この方程式を満たす関数\(x(t)\)を見つけよ」という問題が、微分方程式です。
微分方程式と不定積分・定積分
では、落体の運動方程式\( \frac{d^2 x}{dt^2} =- g\)を一般的に解いてみましょう。
両辺を\(t\)について不定積分します。左辺は、微分と積分が逆関係(微積分学の基本定理)なので、1回微分だけ元に戻って
\[ \begin{aligned}\frac{dx}{dt}(t) = -gt +C_1\end{aligned} \]
となります。\(x(t)\)に関する式を得たいので、もう一度両辺を\(t\)について不定積分すると、
\[ \begin{aligned}x(t) = -\frac{1}{2}gt^2 +C_1 t +C_2\end{aligned} \]
となりました。これは2次関数です。\(t^2\)の係数\(-\frac{1}{2}g\)はマイナスであり、一般的には、次の画像のような挙動を示すでしょう。
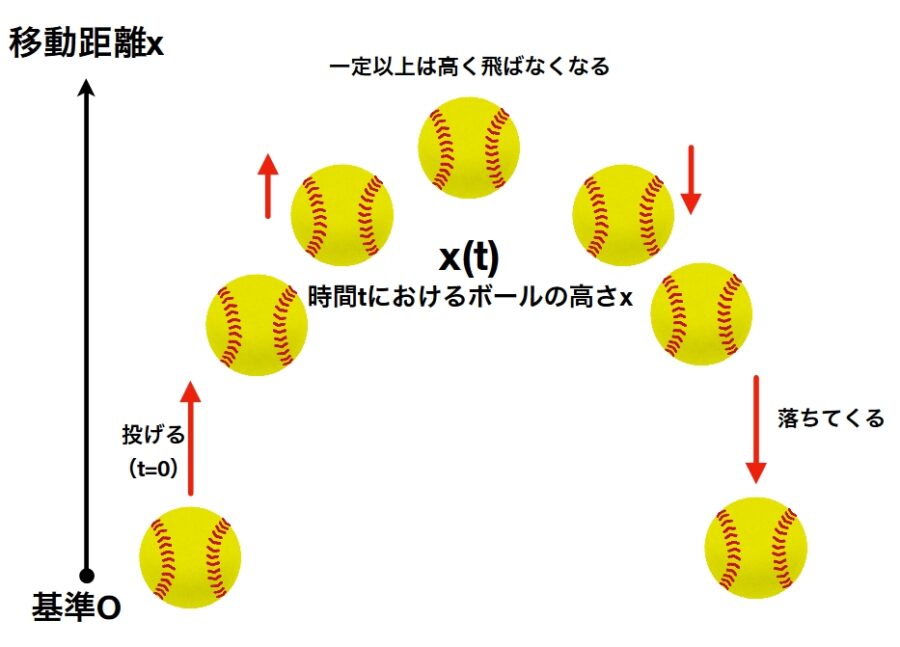
微分方程式を満たす一般的な関数\(x(t) = -\frac{1}{2}gt^2 +C_1 t +C_2\)を、その方程式の一般解と呼びます。
微分方程式の一般解を求める過程で、不定積分を利用するわけですね。
今求めたのは、一般的な落体の運動でした。最初の時刻を\(t=0\)として、初期位置が\(x(0)=x_0\)、初期速度が\(\frac{dx}{dt}(0)=v_0\)であったときの解を求めてみましょう。
一般的な時刻\(t\)における解を求めてみます。そのためには、運動方程式\( \frac{d^2 x}{dt^2} =- g\)を\(t:0 \to t\)について定積分すれば良いです。
結果としては、不定積分で得た式に\(t=0\)のときの条件を代入したものが得られます。
\[ \begin{aligned}\frac{dx}{dt}(0) = -g\cdot 0 +C_1\end{aligned} \]
\[ \begin{aligned}x(0) = -\frac{1}{2} g \cdot 0^2 +C_1 \cdot0 +C_2\end{aligned} \]
整理すれば、積分定数が具体的に\(C_1 = v_0\)、\(C_2 =x_0\)と求まります。したがって、
\[ \begin{aligned}x(t)= -\frac{1}{2}g t^2 + v_0 t +x_0\end{aligned} \]
という解が得られました。
特に、初期位置を\(x_0=0\)とするときは、
\[ \begin{aligned}x(t)= -\frac{1}{2}g t^2 + v_0 t \end{aligned} \]
という式になります。これは高校物理の教科書にも登場する式ですが、微積分を使えば導けるものです。初期速度が\(v_0=0\)のときは、
\[ \begin{aligned}x(t)= -\frac{1}{2}g t^2 \end{aligned} \]
で、非常にシンプルです。
\(t=0\)のときの条件\(x(0)=x_0\)、\(\frac{dx}{dt}(0)=v_0\)を初期条件といい、それを満たす常微分方程式の解を求める問題を初期値問題と呼びます。また、初期値問題を満たす解は、特殊解と呼ばれます。
微分方程式の一般解を得るためには不定積分を使い、特殊解を得るためには定積分を使うことがわかりましたね。
以上、不定積分と定積分をなぜ学ぶかについて、微分方程式とその一般解、特殊解の考え方を紹介してきました。
物体の落下のような問題を含む微分方程式について考えるときに、高校数学の不定積分や定積分の考え方が役立つことを感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
朝倉書店 (2002-01-01T00:00:01Z)
¥6,480
Pearson (2016-03-02T00:00:00.000Z)
¥4,910