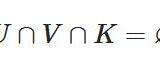どうも、木村(@kimu3_slime)です。
今回は、重み付きグラフ、最小全域木の問題とは何か、そのクラスカル法による解き方を紹介します。
最小全域木の問題とは
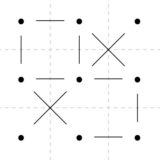
ある地域に、道や電線、通信網など、ネットワークを効率よく作りたいとしましょう。地点と地点の関係が、次のように抽象グラフで表されたとします。
辺は建設可能な経路を表しますが、全頂点がつながったネットワークを考える分に全て使う必要はありません。すべての頂点がつながったまま、サイクルを持たない連結なグラフ=木は、全域木と呼ばれ、その見つけ方は知られています。
とはいえ、与えられたグラフに対し、全域木には複数の選び方、可能性があります。単に全域木を考えるだけでは、そこに効率性の観点がありません。
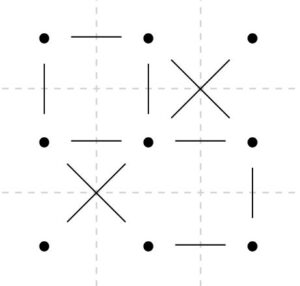
そこで、頂点間を結ぶ経路、グラフの各辺にコストを与えてみましょう。例えば次のように。
グラフ\(G=(V,E)\)のすべての辺にコスト=数字を割り当てるということは、数学的には重み関数(weight function)\(w:E\to \mathbb{R}\)を考えることです。例えば上のグラフならば、左上の辺\(e_1\)の重みは\(w(e_1)=1\)、右下の辺\(e_{11}\)の重みは\(w(e_{11})=3\)といった具合です。
重み関数を持ったグラフ\(G=(V,E,w)\)は、重み付きグラフ(weighted graph)、またはネットワーク(network)と呼ばれます。
重み付きグラフに対しては、そのコストの合計を最小にするような全域木を求める問題が考えられます。つまり、グラフ\(G=(V,E,w)\)に対し、その全域木\(G^{\prime}=(V,E^{\prime})\)で、
\[ \begin{aligned}F(E^{\prime}):=\sum_{e\in E^{\prime}} w(e) \end{aligned} \]
を最小にするものを見つけよ、と。これを最小全域木の問題(minimum spanning tree problem)と呼びます。
ちなみに、すべての辺の重みが1である\(w=1\)ときは、すべての全域木が最小全域木になります。つまり、単に全域木を求める問題になるわけです。最小全域木の問題は、全域木の問題を含んだより一般的な問題と言えます。
クラスカル法による解き方
最小全域木の求め方はいくつか知られていますが、今回はクラスカル法(Kruskal’s algorithm)と呼ばれるものを紹介します。
\(G=(V,E,w)\)を連結な重み付きグラフとする。
辺には次のように番号をつける。
\[ \begin{aligned}w(e_1)\leq w(e_2) \leq \dots \leq w(e_m)\end{aligned} \]
こうして番号付けられた辺\(e_1,e_2,\dots, e_m\)に対し、全域木を求める方法を取る。
この方法は、とにかくコストカットを優先して探索していく単純な方法であり、貪欲法(greedy algorithm)に分類されます。
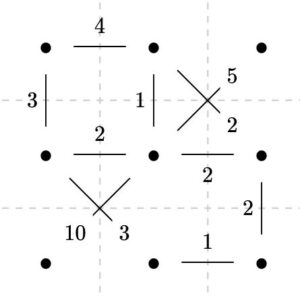
クラスカル法を試してみましょう。まず、コストの小さい順に辺に番号をつけていきます。
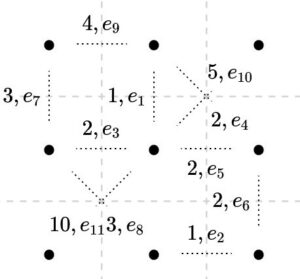
ここから全域木を作っていきます。その手順は、何もないところに番号順に辺を加えていくわけですが、サイクルができてしまう辺は加えない、というものです。
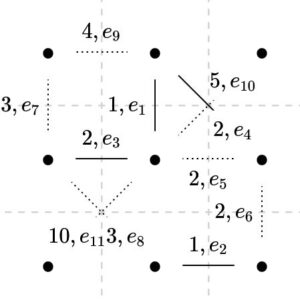
まず\(e_1,\dots,e_4\)が加わります。しかしそこに\(e_5\)を加えるとサイクルができてしまうので、\(e_5\)は加えません。\(w(e_5)=w(e_6)=2\)なので、ここは単にサイクルを作らないだけで、どちらを選んでも問題ない手順ではあります。
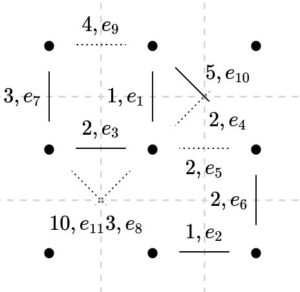
さらに\(e_6,e_7\)は加わりますが、\(e_8,e_9\)はサイクルができてしまうので加わりません。\(w(e_6)\leq w(e_7)\leq w(e_8)\leq w(e_9)\)なので、コストの低い辺がきちんと選ばれていますね。これが最初の並び替えの効果です。
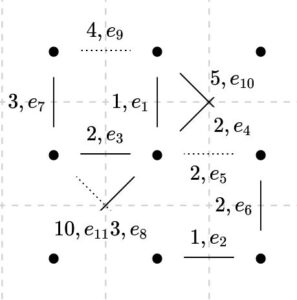
最後に、\(e_{10},e_{11}\)が加わり、すべての辺のチェックが終わります。これは全域木です。コストが\(5,10\)と重い辺は加えたくはありませんが、全頂点をつなげるためにはその辺しか選びようがないわけですね。
\(9\)頂点を含む木は、オイラーの公式により\(9-1=8\)個の辺を必然的に持ちます。この全域木からどの使わない1辺を入れ替えても、コストの総和\(F(E^{\prime})\)は同じか増加するので、最小全域木が求められました。
クラスカル法によって一般のケースで最小全域木を求められていることの証明については、「離散数学への招待〈上〉」を参照してください。
以上、重み付きグラフ、最小全域木の問題とは何か、そのクラスカル法による作り方を紹介してきました。
クラスカル法は辺のすべてをチェックするため、辺の数が増えたときに時間がかかりそうですが、それでもこの単純な方法で原理的に解ける、とわかるのは嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京 (2002-12T)
¥1,773 (中古品)
丸善出版 (2012-07-17T00:00:01Z)
¥11,800 (中古品)
Graph Theory (Graduate Texts in Mathematics)
Springer (2018-06-05T00:00:01Z)
¥6,933