どうも、木村(@kimu3_slime)です。
今回は、平面グラフ、面とは何か、クラトフスキーの定理を紹介します。
平面グラフとは
これまで考えてきたグラフは、単に頂点と辺の集まりであり、それが平面に描いたときにどんな面を形成するか、といったことを考えませんでした。平面グラフと対比させて、それを抽象グラフ(abstract graph)と言います。
平面グラフ(plane graph)\(G=(E,V)\)は、抽象グラフより特殊な定式化をします。
- 頂点は、平面の有限個の点の集まりである。\(V \subset \mathbb{R}^2\)
- \(p,q\)をつなぐ辺とは、弧\(c(t) = (1-t)p+tq \), \(0\leq t \leq 1\)のことである。
- 異なる辺は、異なる端点を持つ。(グラフの単純性)
- 辺の内部\(\{c(t) \subset \mathbb{R}^2 \mid 0<t<1\}\)は、他の頂点や辺を含まない。例えば、辺と辺が交差しない。
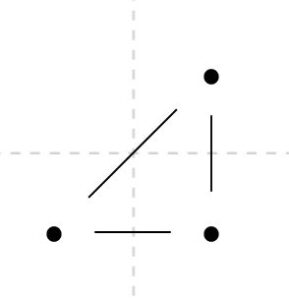
例えば、上の図は平面グラフとして表せます。3つの頂点を、\(V=\{(0,0),(1,0),(1,1)\}\)としましょう。\((0,0),(1,0)\)をつなぐ辺は、\(c_1(t)=(t,0)\)と表せます。原点から時刻\(t=0\)に出発して、\(t=1\)で\((1,0)\)に到着するイメージですね。他の辺も同様に表せます。
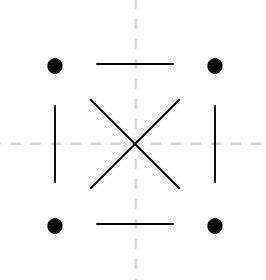
上の図で表されるグラフは、平面グラフではありません。交差する辺を持っているからです。ただし、抽象グラフではあります。平面グラフでは、抽象グラフでは考えることができなかった、辺の交差について考えることができます。
実は、この抽象グラフ\(K_4\)は、描き方を変えることで平面グラフとして表すことができます。どの頂点も、他の\(3\)頂点と辺でつながっていますね。
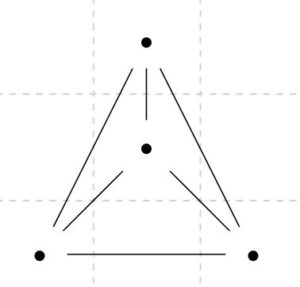
平面的グラフとして表せる抽象グラフは、平面的グラフ(planer graph)と呼ばれます。これは詳しくは、抽象グラフの平面埋め込み、グラフの描写と呼ばれる話です。
平面グラフの面とは
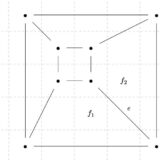
平面グラフでは辺が交差しないので、辺が囲んでいる領域、すなわち面を考えることができます。
例えば、上のグラフならば、グラフの「内側」に3つの面があり、外側に大きく広がった1つの面があります。
一般に、有限個の線分をあわせた平面の部分集合で、円周\(S^1\)に同相なものを多角形(polygon)と呼びます。三角形や四角形は、「連続的に」変形することで、円に変えることができますね。(同相について、詳しくは別記事で。)
多角形があると、平面は必ず2つの領域に分かれることが知られています。当たり前に思えることですが、定理として示せるものです。
多角形に関するジョルダンの曲線定理(Jordan Curve Theorem)
すべての多角形\(P \subset \mathbb{R}^2\)に対し、平面から多角形を除いた集合\(\mathbb{R}^2 \backslash P\)はちょうどふたつの領域を持つ。それぞれの領域の境界は、その多角形\(P\)となっている。
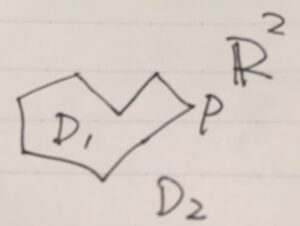
この定理により、平面\(\mathbb{R}^2\)から平面グラフ\(G\)を除いた集合は、有限個の連結な開集合(領域)に分かれるので、それらを面(face)と呼ぶわけです。
平面グラフは有限個の点からなるものを考えているので、必ず有界な集合になり、ひとつの大きな円盤に含まれます。その内側にある面を内面(inner face)、外側を含む面を外面(outer face)と呼びます。
(ジョルダンの曲線定理は、多角形ではなく、もっと一般の曲線=単純閉曲線について成り立ちます。平面が閉曲線によって2つの領域に分かれるという事実は、複素解析でも利用されています。)
平面グラフを考えることで、グラフと面の性質の問題を考えることができます。
例えば、グラフの一種:木は、必ず平面グラフとして捉えられますが、内面はなく、外面1つのみがあります。木の頂点と辺の個数について、オイラーの公式\(\mathrm{card}(V)=\mathrm{card}(E) +1\)が成り立つことを紹介しました。これは面の数を考慮した、平面グラフにおけるオイラーの公式として一般化されます。
「日本地図で隣り合った県を異なる何色の色で塗り分けられるか?」というような問題は、平面グラフにおける地図の塗り分け問題として知られています。特に、「任意の平面グラフを4色で必ず塗り分けられるか?」という問題は四色問題と呼ばれ、コンピュータを駆使して有限個のケースをチェックして証明された話が有名です。
クラトフスキーの定理
4頂点ですべての頂点間に辺がある抽象グラフ\(K_4\)は、一見平面グラフでないように見えたものの、実際は平面的でした。
グラフといえば平面に描けるものなのだから、すべては平面グラフなのではないか? そう考えるのは、間違いです。平面グラフでない抽象グラフの例として、次の2つ、\(K_5\)と\(K_{3,3}\)が知られています。
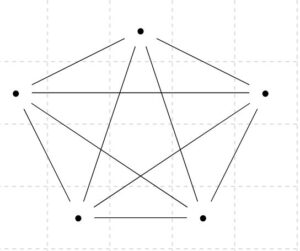
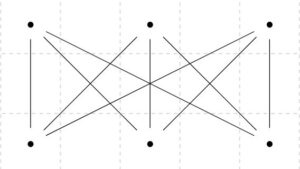
これらの抽象グラフは、平面に描こうとするとどうやっても辺の交差が生まれてしまうのです。一般に、次の定理が知られています。
クラトフスキーの定理(Kuratowski’s theorem)、ワグナーの定理(Wagner’s theorem)
抽象グラフ\(G\)が平面的であることは、\(G\)が\(K_5\)または\(K_{3,3}\)をマイナーとして含まないことと同値。
特に、\(G\)が\(K_5\)または\(K_{3,3}\)を部分グラフとして含むならば、\(G\)は平面的でない。
\(K_4\)が平面的であるのに対して、頂点が1つ増えた\(K_5\)が平面的でなくなるのは、不思議な感じがしますね。
マイナーといった用語、定理の証明については、「離散数学への招待〈上〉」または「Graph Theory」を参照してください。
以上、平面グラフ、面、クラトフスキーの定理について紹介してきました。
平面グラフに伴う話題、オイラーの公式や四色問題は有名で、聞いたことがある人も多いのではないでしょうか。その基礎として、そもそも平面グラフとはどういうものか、知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京 (2002-12T)
¥1,773 (中古品)
丸善出版 (2012-07-17T00:00:01Z)
¥11,800 (中古品)
Graph Theory (Graduate Texts in Mathematics)
Springer (2018-06-05T00:00:01Z)
¥6,933